ملاحظات مش بندی برای مسائل استاتیک خطی

در این مطلب وبلاگ، ملاحظات مش بندی را برای مسائل المان محدود استاتیک خطی معرفی می کنیم. این اولین پست از یک سری پست در مورد تکنیک های مش بندی است که به منظور ارائه راهنمایی در مورد نحوه نزدیک شدن به مش بندی مدل اجزای محدود شما با اطمینان است.

درباره مش بندی عناصر محدود

مش المان محدود دو هدف را دنبال می کند. ابتدا هندسه CAD مدل‌سازی شده را به قطعات یا عناصر کوچک‌تر تقسیم می‌کند ، که می‌توان مجموعه‌ای از معادلات را که جواب معادله حاکم را توصیف می‌کنند، نوشت. مش همچنین برای نشان دادن میدان حل به فیزیک در حال حل استفاده می شود. خطا در ارتباط با گسسته سازی هندسه و همچنین گسسته سازی راه حل وجود دارد، بنابراین اجازه دهید این موارد را جداگانه بررسی کنیم.

گسسته سازی هندسی

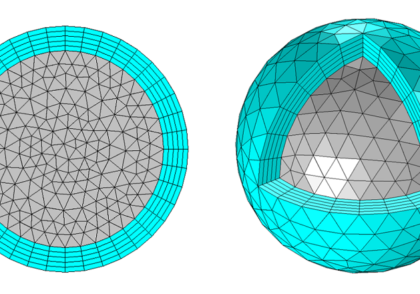
دو هندسه بسیار ساده، یک بلوک و یک پوسته استوانه ای را در نظر بگیرید:

چهار نوع مختلف از عناصر وجود دارد که می‌توان از آنها برای درهم‌بندی این هندسه‌ها استفاده کرد – چهار وجهی (تتس)، هگزادر (آجر)، منشورهای مثلثی (منشور)، و عناصر هرمی:

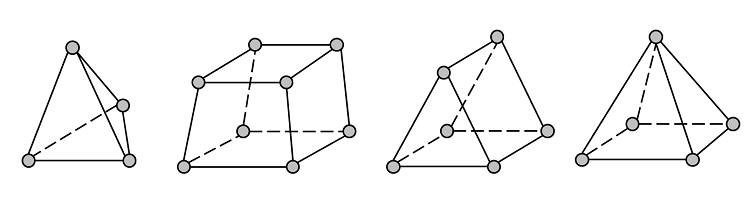
دایره های خاکستری نشان دهنده گوشه ها یا گره های عناصر هستند. هر ترکیبی از چهار عنصر فوق را می توان استفاده کرد. (برای مدل‌سازی دو بعدی، عناصر مثلثی و چهار ضلعی در دسترس هستند.) با بررسی می‌توانید ببینید که هر دوی این هندسه‌ها را می‌توان با یک عنصر آجری، دو منشور، سه هرم، یا پنج تت در هم آمیخت. همانطور که در پست قبلی وبلاگ در مورد حل مسائل المان محدود استاتیک خطی یاد گرفتیم ، همیشه در یک تکرار نیوتن-رافسون به یک راه حل خواهید رسید. این برای مسائل المان محدود خطی بدون در نظر گرفتن مش صادق است. بنابراین بیایید نگاهی به ساده‌ترین شبکه‌ای که می‌توانیم روی این سازه‌ها قرار دهیم بیندازیم. در اینجا نموداری از یک عنصر آجری منفرد است که این هندسه ها را گسسته می کند:

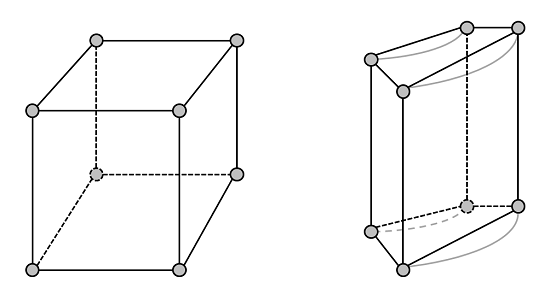
مش بلوک آشکارا نمایانگر کامل هندسه واقعی است، در حالی که مش پوسته استوانه ای بسیار ضعیف به نظر می رسد. در واقع، فقط در هنگام ترسیم به این شکل ظاهر می شود. عناصر همیشه به صورت دارای لبه های مستقیم بر روی صفحه نمایش داده می شوند (این کار برای اهداف عملکرد گرافیکی انجام می شود) اما COMSOL معمولاً از یک عنصر لاگرانژی درجه دوم برای گسسته کردن هندسه (و راه حل) استفاده می کند. بنابراین اگرچه لبه های عنصر همیشه مستقیم به نظر می رسند، اما در داخل به صورت زیر نمایش داده می شوند:

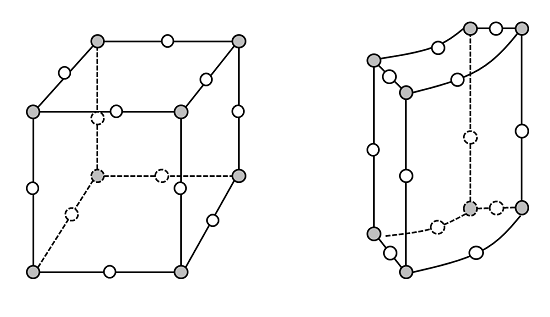
دایره های سفید نشان دهنده گره های نقطه میانی این لبه های عنصر درجه دوم هستند. یعنی خطوطی که لبه‌های عناصر را مشخص می‌کنند با سه نقطه نشان داده می‌شوند و یال‌ها از طریق یک تناسب چند جمله‌ای تقریبی می‌شوند. همچنین گره های اضافی در مرکز هر یک از این وجوه چهار ضلعی و در مرکز حجم برای این عناصر شش وجهی لاگرانژی مرتبه دوم (برای وضوح حذف شده است) وجود دارد. واضح است که این عناصر عملکرد بهتری در نمایش مرزهای منحنی عناصر دارند. به‌طور پیش‌فرض، COMSOL از عناصر درجه دوم برای بیشتر فیزیک استفاده می‌کند، دو استثناء، مشکلات مربوط به انتقال گونه‌های شیمیایی و هنگام حل یک میدان جریان سیال هستند. (از آنجایی که این نوع مشکلات همرفت هستندمعادلات حاکم با عناصر مرتبه اول بهتر حل می شوند. عناصر مرتبه بالاتر نیز در دسترس هستند، اما عناصر مرتبه دوم پیش فرض معمولاً سازش خوبی بین دقت و الزامات محاسباتی را نشان می دهند.

شکل زیر خطای گسسته سازی هندسی را هنگام مش بندی یک قوس 90 درجه بر حسب تعداد عناصر مرتبه اول و دوم نشان می دهد:

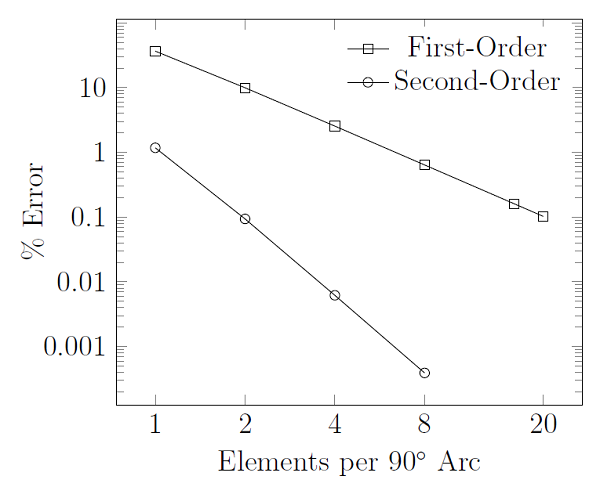
نتیجه ای که می توان از این موضوع گرفت این است که حداقل دو عنصر مرتبه دوم یا حداقل هشت عنصر مرتبه اول برای کاهش خطای گسسته هندسی زیر 1٪ مورد نیاز است. در واقع، دو عنصر مرتبه دوم خطای گسسته هندسی کمتر از 0.1٪ را معرفی می کنند. مش های ظریف تر هندسه را با دقت بیشتری نشان می دهند، اما منابع محاسباتی بیشتری را می طلبند. این چند دستورالعمل عملی خوب به ما می دهد:

1. هنگام استفاده از عناصر درجه یک، مش را طوری تنظیم کنید که حداقل هشت عنصر در قوس 90 درجه وجود داشته باشد.
2. هنگام استفاده از عناصر درجه دوم، از دو عنصر در قوس 90 درجه استفاده کنید

با استفاده از این قوانین سرانگشتی، اکنون می‌توانیم خطای معرفی‌شده را با درهم کردن هندسه تخمین بزنیم، و می‌توانیم قبل از اینکه مدل را حل کنیم، با کمی اطمینان این کار را انجام دهیم. حال بیایید توجه خود را به این معطوف کنیم که چگونه مش راه حل را گسسته می کند.

گسسته سازی راه حل

مش المان محدود نیز برای نشان دادن میدان حل استفاده می شود. راه‌حل در نقاط گره محاسبه می‌شود و از یک پایه چند جمله‌ای برای درون‌یابی این راه‌حل در سراسر عنصر برای بازیابی کل میدان حل استفاده می‌شود. هنگام حل مسائل اجزای محدود خطی، ما همیشه قادر به محاسبه یک راه حل هستیم، مهم نیست که مش چقدر درشت باشد، اما ممکن است خیلی دقیق نباشد. برای درک اینکه چگونه چگالی مش بر دقت محلول تاثیر می گذارد، اجازه دهید به یک مسئله انتقال حرارت ساده در هندسه های قبلی خود نگاه کنیم:

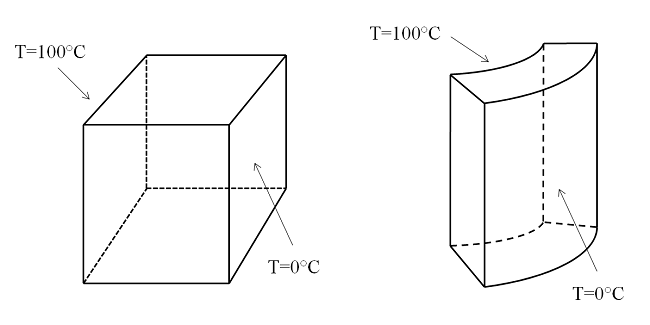
اختلاف دما در وجوه مخالف بلوک و پوسته استوانه ای اعمال می شود. هدایت حرارتی ثابت است و تمام سطوح دیگر عایق حرارتی هستند.

راه حل برای مورد بلوک مربع این است که میدان دما به صورت خطی در سراسر بلوک تغییر می کند. بنابراین برای این مدل، یک عنصر منفرد، مرتبه اول، شش وجهی در واقع برای محاسبه جواب واقعی کافی است. البته به ندرت اینقدر خوش شانس خواهید بود!

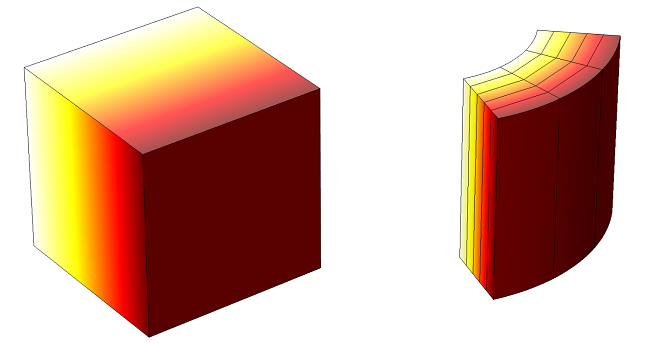
بنابراین، بیایید به مورد کمی چالش برانگیزتر نگاه کنیم. قبلاً دیده‌ایم که مدل پوسته استوانه‌ای به دلیل لبه‌های منحنی دارای خطای گسسته‌سازی هندسی خواهد بود، بنابراین ما این مدل را با حداقل دو عنصر مرتبه دوم (یا هشت درجه اول) در امتداد لبه‌های منحنی شروع می‌کنیم. اگر به نمودار بالا دقت کنید، می بینید که لبه های عنصر روی مرزها منحنی هستند، در حالی که عناصر داخلی دارای لبه های مستقیم هستند.

در امتداد محور سیلندر، می توانیم از یک عنصر استفاده کنیم، زیرا میدان دما در این جهت تغییر نخواهد کرد. با این حال، در جهت شعاعی، از سطح داخلی به بیرون، همچنین باید عناصر کافی برای گسسته کردن محلول را داشته باشیم. راه حل تحلیلی برای این مورد به شرح زیر استو می توان با حل المان محدود ما مقایسه کرد. از آنجایی که توابع پایه چند جمله ای نمی توانند تابع را به طور کامل توصیف کنند، بیایید خطا را در حل المان محدود برای هر دو عنصر خطی و درجه دوم رسم کنیم:

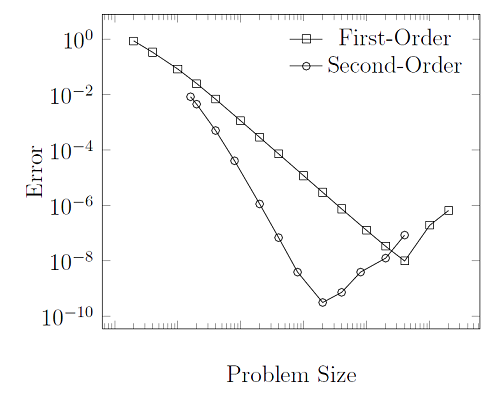
چیزی که از این نمودار می بینید این است که با افزایش تعداد عناصر در مدل، خطا کاهش می یابد. این یک ویژگی اساسی روش اجزای محدود است : هرچه عناصر بیشتر باشد، راه حل شما دقیق تر است. البته هزینه ای نیز در این رابطه وجود دارد. منابع محاسباتی بیشتری، هم زمان و هم سخت افزار، برای حل مدل های بزرگتر مورد نیاز است. اکنون، متوجه خواهید شد که هیچ واحدی در محور x این نمودار وجود ندارد و این عمد است. سرعت کاهش خطا با توجه به پالایش مش برای هر مدل متفاوت است و به عوامل زیادی بستگی دارد. تنها نکته مهم این است که برای مشکلاتی که به خوبی مطرح شده اند، همیشه به صورت یکنواخت پایین می آید.

همچنین متوجه خواهید شد که پس از یک نقطه، خطا شروع به بازگشت به بالا می کند. این زمانی اتفاق می‌افتد که تک تک عناصر مش شروع به کوچک شدن کنند و ما به محدودیت‌های دقت عددی برسیم . یعنی اعداد در مدل ما کوچکتر از آن چیزی است که بتوان به طور دقیق در رایانه نشان داد. این یک مشکل ذاتی در همه روش های محاسباتی است، نه فقط روش اجزای محدود. کامپیوترها نمی توانند تمام اعداد واقعی را به طور دقیق نشان دهند. نقطه ای که در آن خطا شروع به بازگشت به بالا می کند، در اطراف خواهد بودو برای اطمینان و عملی بودن، اغلب می گوییم که حداقل خطای قابل دستیابی 10 ^-6 است . بنابراین، اگر تفاوت مقیاس شده بین راه حل واقعی و محاسبه شده را در کل مدل ادغام کنیم:

ما می گوییم که خطا،، معمولاً می تواند به اندازه 10 ^-6 در محدوده پالایش مش ساخته شود. در عمل، ورودی‌های مدل‌های ما معمولاً عدم قطعیت بسیار بیشتری از این دارند. همچنین به خاطر داشته باشید که به طور کلی ما راه حل واقعی را نمی دانیم، در عوض باید راه حل های محاسبه شده را بین مش های با اندازه های مختلف مقایسه کنیم و مشاهده کنیم که راه حل به چه مقادیری همگرا می شود.

اصلاح مش تطبیقی

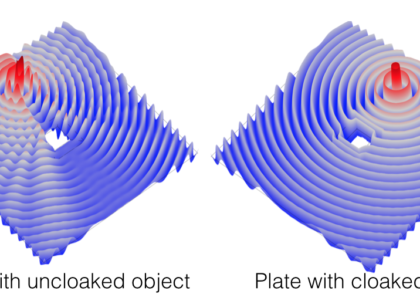
من می خواهم این پست وبلاگ را با معرفی روشی بهتر برای اصلاح مش ببندم. نمودارهای بالا نشان می دهد که با کوچکتر شدن تمام عناصر مدل، خطا کاهش می یابد. با این حال، در حالت ایده‌آل، فقط در مناطقی که خطا زیاد است، عناصر را کوچک‌تر می‌کنید. COMSOL از طریق Adaptive Mesh Refinement به این موضوع می پردازد، که ابتدا روی یک مش اولیه حل می شود و به طور مکرر عناصر را در مناطقی که خطا تخمین زده می شود زیاد وارد می کند و سپس مدل را دوباره حل می کند. این را می توان برای هر تعداد تکرار به دلخواه ادامه داد. این قابلیت با عناصر مثلثی به صورت دو بعدی و چهار وجهی به صورت سه بعدی کار می کند. بیایید این مشکل را در زمینه یک مسئله مکانیک سازه ساده بررسی کنیم – صفحه تحت کشش تک محوری با یک سوراخ، همانطور که در شکل زیر نشان داده شده است. با استفاده از تقارن، تنها یک چهارم مدل باید حل شود.

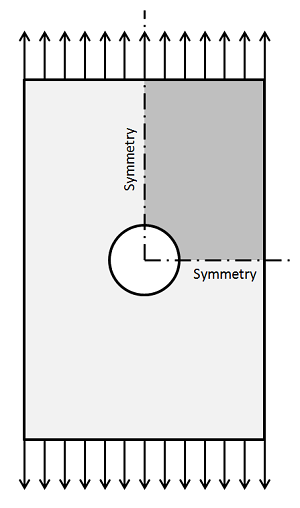
میدان‌های جابجایی محاسبه‌شده و تنش‌های حاصل، در فاصله‌ای دورتر از سوراخ کاملاً یکنواخت هستند، اما در نزدیکی آن‌ها به شدت متفاوت هستند. شکل زیر یک مش اولیه و همچنین نتایج چندین تکرار پالایش مش تطبیقی ​​را به همراه میدان تنش محاسبه شده نشان می دهد.

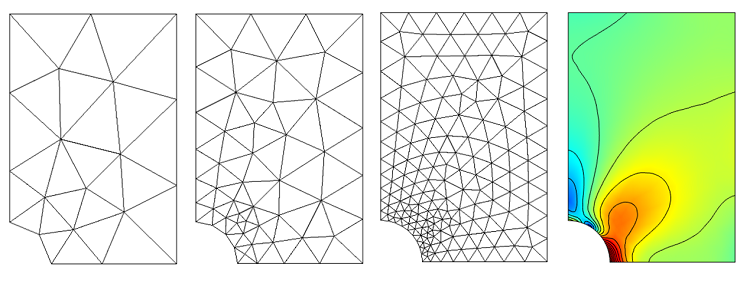
توجه داشته باشید که چگونه COMSOL ترجیحاً عناصر کوچکتر را در اطراف سوراخ قرار می دهد. این نباید تعجب آور باشد، زیرا از قبل می دانیم که تنش های بیشتری در اطراف سوراخ وجود خواهد داشت. در عمل، استفاده از ترکیبی از پالایش مش تطبیقی، قضاوت مهندسی و تجربه برای یافتن یک مش قابل قبول توصیه می شود.

خلاصه نکات اصلی

• شما همیشه می خواهید یک مطالعه اصلاح مش انجام دهید و نتایج را روی مش های با اندازه های مختلف مقایسه کنید
• از دانش خود در مورد خطای گسسته سازی هندسی استفاده کنید تا تا حد امکان یک مش شروع درشت انتخاب کنید و از آنجا اصلاح کنید.
• می توانید از پالایش مش تطبیقی ​​یا قضاوت مهندسی خودتان برای اصلاح مش استفاده کنید.