استفاده از بهینه سازی بدون گرادیان

ماژول بهینه سازی COMSOL شامل تکنیک های بهینه سازی مبتنی بر گرادیان و بدون گرادیان است. در حالی که روش بهینه‌سازی مبتنی بر گرادیان می‌تواند یک مشتق تحلیلی دقیق از یک تابع هدف و هر توابع محدودیت مرتبط را محاسبه کند، نیاز دارد که این توابع صاف و قابل تمایز باشند. در این پست وبلاگ، استفاده از بهینه‌ساز بدون گرادیان را بررسی می‌کنیم که می‌تواند تابع هدف و محدودیت‌هایی را که قابل تمایز یا صاف نیستند در نظر بگیرد. ابعاد یک چرخ ریسندگی برای کاهش جرم و در عین حال حفظ محدودیت در تنش اوج در قطعه بهینه شده است.

استرس در چرخ چرخان

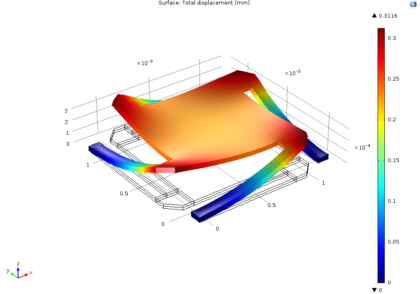
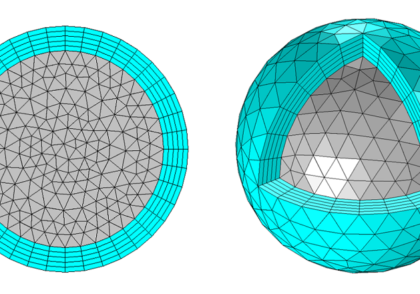
یک چرخ ریسنده تنش های گریز از مرکز را تجربه می کند که منجر به تنش در سراسر قطعه می شود. یک الگوی منظم از سوراخ ها برای کاهش جرم در توپی چرخ بریده شده است. تنش های فون میزس ناشی از نیروهای گریز از مرکز نشان داده شده است. مطلوب است که جرم را بیشتر کاهش دهیم، در حالی که تنش ها را زیر یک مقدار بحرانی نگه داریم.

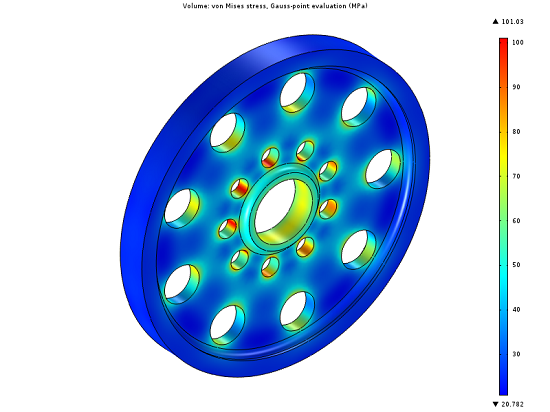
حل استرس ها

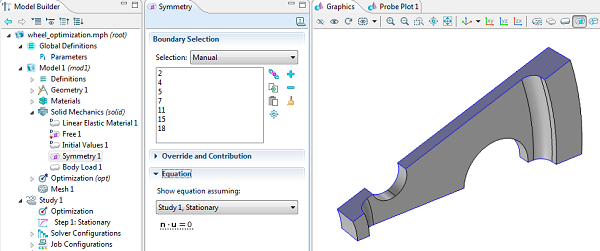
اگرچه می‌توانیم کل چرخ را به یکباره مدل‌سازی کنیم، اما تقارن آینه‌ای و چرخشی در این قسمت وجود دارد که باعث می‌شود مدل را کاهش دهیم و در نتیجه نیازهای محاسباتی را به حداقل برسانیم. شرایط مرزی تقارن برای مهار قطعه استفاده می شود.

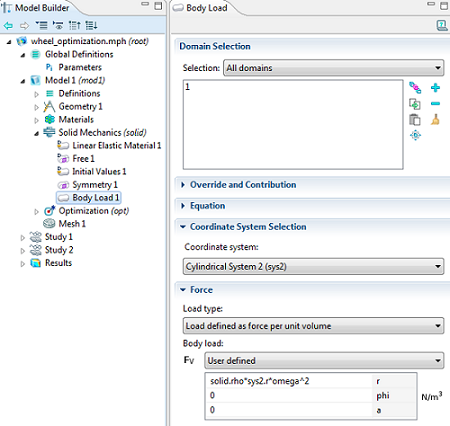
یک بار بدنه بر حسب سرعت دورانی، محور چرخشی و چگالی مواد برای مدل‌سازی نیروی گریز از مرکز اعمال می‌شود. مدل با استفاده از حلگر ثابت، یعنی با فرض یک سرعت چرخشی ثابت حل می شود.

انتخاب متغیرهای طراحی

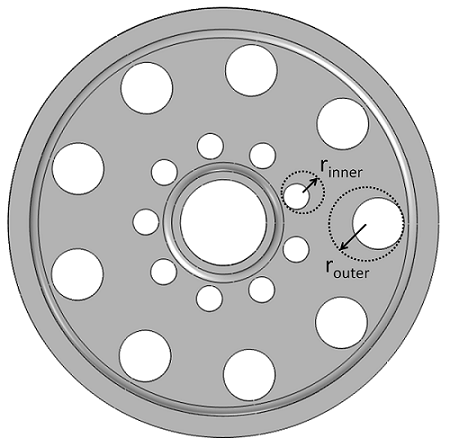
در این مورد، بیایید فرض کنیم که در حال حاضر یک فرآیند ساخت وجود دارد، و ما می خواهیم حداقل تغییری را در طراحی کلی قطعه ایجاد کنیم تا هزینه های ابزارآلات مجدد را کاهش دهیم. یک انتخاب طبیعی از متغیرهای طراحی، تغییر شعاع سوراخ ها در توپی است. بنابراین، ما به دنباله هندسه برمی گردیم و هم شعاع سوراخ ها و هم مکان آنها را پارامتر می کنیم. ما همچنین می‌توانیم بر اساس یک تحلیل هندسی محض بفهمیم که در حداکثر شعاع هر سوراخ باید مرزهایی وجود داشته باشد، در غیر این صورت نواحی بین سوراخ‌ها خیلی نازک می‌شوند و سوراخ‌ها روی هم قرار می‌گیرند. از آنجایی که نمی‌خواهیم سوراخ‌ها به طور کامل ناپدید شوند، یک کران را نیز روی حداقل شعاع قرار می‌دهیم.

تعریف تابع هدف و محدودیت ها

هدف بهینه‌سازی در اینجا صرفاً کاهش جرم قطعه است که انتگرال چگالی مواد در تمام حوزه‌ها است.

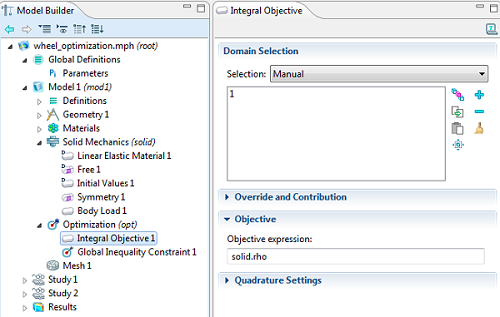
هدف بهینه سازی به حداقل رساندن جرم، انتگرال چگالی است.

محدودیت کمی پیچیده تر است. ما می خواهیم استرس اوج را در قطعه به حداقل برسانیم. با این حال، ما از قبل نمی دانیم که اوج استرس کجا خواهد بود. اگر سوراخ های داخلی یا بیرونی را خیلی کوچک کنیم، منجر به تمرکز تنش در اطراف سوراخ می شود. اگر هر یک از شعاع ها را خیلی بزرگ کنیم، ماده بین سوراخ ها می تواند خیلی نازک شود و همچنین منجر به تنش های زیاد شود. بنابراین، ما باید حداکثر تنش را در سراسر قطعه کنترل کنیم و آن را به زیر تنش پیک مشخص محدود کنیم. این یک محدودیت غیر قابل تمایز است و به طور خاص به روش بهینه‌سازی بدون گرادیان نیاز دارد.

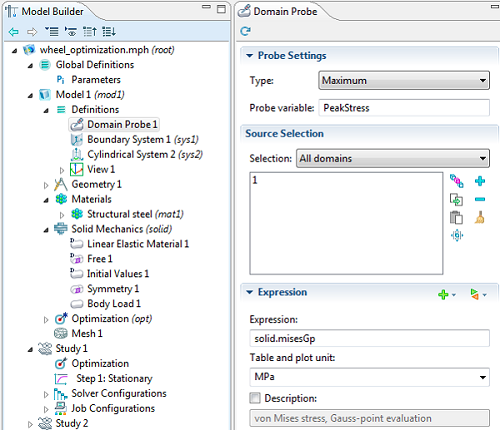
استرس اوج از طریق یک Domain Probe نظارت می شود و نام PeakStress داده می شود.

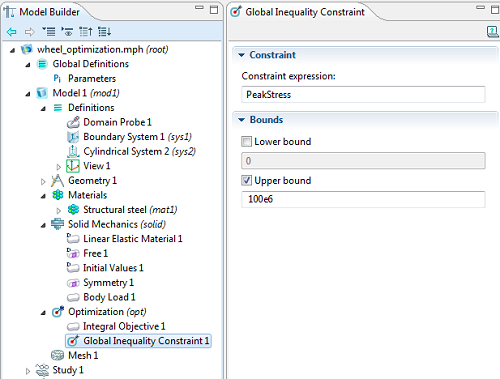
متغیر تنش اوج محدود به ماندن در محدوده بالایی است.

حل مسئله با روش بهینه سازی بدون گرادیان

برای حل مشکل بهینه سازی، یک ویژگی Optimization به Study Branch اضافه می شود. روش Nelder-Mead یکی از دو روش بدون گرادیان است (یکی دیگر جستجوی مختصات است ). الگوریتم‌های بهینه‌سازی بدون گرادیان همچنین به هندسه اجازه می‌دهند تا با تغییر ابعاد، دوباره مشبک شود.

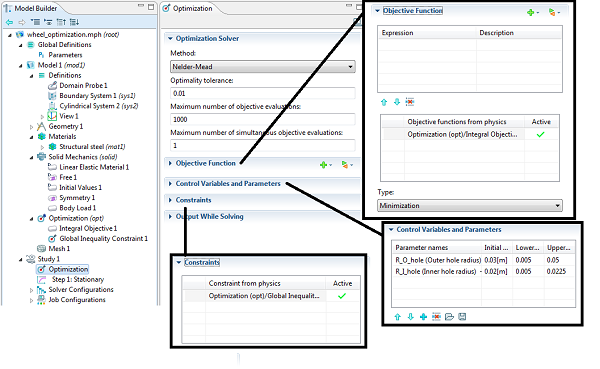
تابع هدف و محدودیت از شاخه Optimization در درخت مدل تعریف شده است. به متغیرهای کنترلی شرایط اولیه داده می شود و ما کران های بالا و پایین را مشخص می کنیم. طراحی بهینه به طور قابل توجهی متفاوت است – جرم 20٪ کاهش می یابد و در عین حال محدودیت در تنش اوج حفظ می شود.