در تحلیل حالت معمولاً هدف اصلی یافتن یک ثابت انتشار است . این مقدار اغلب، اما نه همیشه، ارزش واقعی دارد. اگر تجزیه و تحلیل شامل قسمتی با تلفات باشد، مانند یک رسانایی غیرصفر یا یک مرز باز، مقدار ویژه پیچیده است. در چنین شرایطی، بخش واقعی و خیالی تفاسیر جداگانه ای دارند:
مقدار ویژه است. برای مسائل هارمونیک زمانی، میدان الکتریکی برای انتشار خارج از صفحه را می توان به صورت نوشتاری نوشت
پارامتر فضایی، α = δ z + j β = -λ ، می تواند یک قسمت واقعی و یک قسمت خیالی داشته باشد. ثابت انتشار برابر با قسمت خیالی است و قسمت واقعی δ z نشان دهنده میرایی در جهت انتشار است.
این مدل دو بعدی حالتهای یک موجبر دایرهای با دیوارههای ساختهشده از یک هادی غیر کامل را پیدا میکند که در این مورد مس است. تلفات در دیوارها منجر به تضعیف موج انتشار می شود. ثابت انتشار β به عنوان قسمت فرضی α = – λ و میرایی δ z به عنوان قسمت واقعی به دست می آید. از آنجایی که موج در موجبر در جهت z به صورت e -δ zz ضعیف می شود ، میرایی در مقیاس دسی بل با استفاده از فرمول محاسبه می شود.
حل کننده مقدار ویژه شش مقدار ویژه را برمی گرداند. جدول 1 شش شاخص حالت موثر را نشان می دهد، n eff ، نزدیکترین به 1، که در آن
و k 0 عدد موج در خلاء است. جدول همچنین ثابت انتشار و میرایی را بر حسب dB/m برای هر حالت ویژه فهرست می کند.
نمودار سطح پیش فرض هنجار میدان الکتریکی را برای شاخص حالت موثر 0.9308 – 2.208·10 – 6 j نشان می دهد . این نمودار در شکل 1 نشان داده شده است .
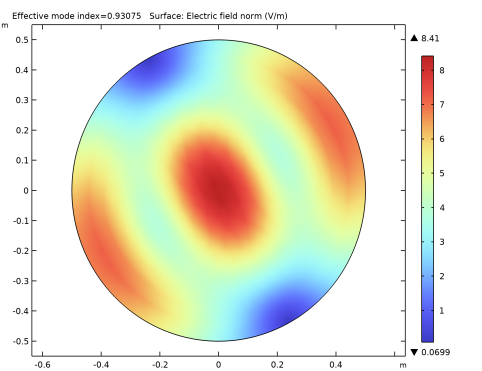
شکل 1: نمودار سطح هنجار میدان الکتریکی را برای شاخص حالت موثر 0.9308 – 2.208·10 -6 j به تصویر می کشد.
5 |
1 |
نمودار پیش فرض هنجار میدان الکتریکی را برای کمترین حالت یافت شده نشان می دهد. با شکل 1 مقایسه کنید .
2 |
4 |




