Mooney-Rivlin Curve Fit
معرفی
این مدل آموزشی نحوه استفاده از ماژول بهینه سازی را برای تخمین پارامترهای تابع ناشناخته بر اساس داده های اندازه گیری شده نشان می دهد. مدل ماده جامد دو پارامتری Mooney-Rivlin به عنوان مثال استفاده می شود، اما این روش به طور کلی زمانی قابل استفاده است که شما نیاز دارید که یک تابع تحلیلی پارامتری را برای داده های اندازه گیری شده تنظیم کنید.
توجه: این برنامه در مقدمه ماژول بهینه سازی نیز استفاده می شود .
تعریف مدل
مدل مواد تراکم ناپذیر دو پارامتری Mooney-Rivlin رفتار محلی مواد لاستیک مانند را توصیف می کند. مدل فرض می کند که چگالی انرژی کرنش محلی در یک جامد تراکم ناپذیر تابعی ساده از متغیرهای کرنش محلی است.
در یک آزمایش کششی استاندارد، یک نمونه آزمایش متقارن دورانی به گونه ای کشیده می شود که در یک جهت امتداد یافته و در دو جهت دیگر به طور متقارن منقبض می شود. برای این مورد امتداد تک محوری، رابطه بین نیروی اعمال شده، F و امتداد حاصل، ΔL ، یک ماده مونی-ریولین واقعی است.
(1)
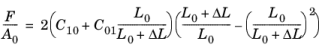
که در آن A 0 سطح مقطع اولیه نمونه آزمایش و L 0 طول مرجع آن است. ثابت های C 10 و C 01 پارامترهای ماده ای هستند که باید با برازش معادله 1 به داده های تجربی از آزمون کشش تعیین شوند .
در عمل، داده های آزمون کشش به شکلی ارائه می شود که مستقل از هندسه نمونه آزمایشی مورد استفاده است. چندین فرمت ممکن وجود دارد. مورد استفاده شده در اینجا حاوی مقادیر اندازه گیری شده متناظر تنش مهندسی، P i است که نشان دهنده نیرو در واحد سطح مرجع است.
و کشش، λ i ، نشان دهنده ازدیاد طول نسبی است
رابطه مورد انتظار بین این متغیرها برای یک ماده Mooney-Rivlin است
با توجه به N جفت اندازه گیری (λi ، Pi ) ، i = 1 ، … ، N ، مقادیر C 10 و C 01 که به بهترین وجه با داده های اندازه گیری شده مطابقت دارند، مقادیری در نظر گرفته می شوند که مجذور خطای کل را به حداقل می رساند.
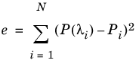
بنابراین مسئله برازش منحنی با یک مسئله بهینه سازی یکسان است.
نتایج
شکل 1 تنش و تنش اندازه گیری شده را نشان می دهد که با استفاده از خواص مواد که به داده های اندازه گیری شده برازش شده اند محاسبه شده اند.
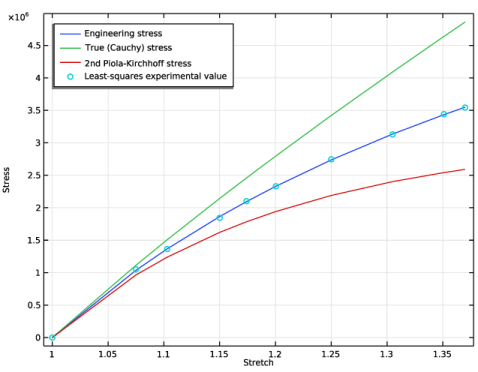
شکل 1: تنش های مهندسی اندازه گیری شده (دایره های فیروزه ای) و محاسبه شده (خط آبی). علاوه بر این، دو معیار استرس دیگر برای مقایسه ترسیم شده است.
لازم به ذکر است که برای کشش های بزرگ، مقادیر تنش های مختلف به طور قابل توجهی متفاوت خواهد بود. برای یک حالت تنش تک محوری و یک ماده تراکم ناپذیر مانند این مورد، تنش واقعی (تنش کوشی؛ تنش در هر ناحیه جریان) با تنش مهندسی مرتبط است.
(2)
تنش دوم Piola-Kirchhoff به این صورت تعریف می شود
(3)
بنابراین لازم است به معیارهای تنش مورد استفاده در زمانی که یک تفسیر از یک شبیهسازی واقعی که در آن یک مدل ماده برای کششهای بزرگ استفاده میشود، استفاده شود، توجه شود.
مسیر کتابخانه برنامه: Optimization_Module/Parameter_Estimation/curve_fit_mooney_rivlin
دستورالعمل های مدل سازی
از منوی File ، New را انتخاب کنید .
جدید
در پنجره جدید ، روی  Blank Model کلیک کنید .
Blank Model کلیک کنید .
افزودن کامپوننت
در نوار ابزار Home ، روی  Add Component کلیک کنید و 0D را انتخاب کنید .
Add Component کلیک کنید و 0D را انتخاب کنید .
تعاریف جهانی
پارامتر کشش لامبدا را که در داده های اندازه گیری شده تغییر کرده است، اضافه کنید. همچنین پارامترهای مواد ناشناخته را به عنوان پارامترهای مدل جهانی اضافه کنید.
پارامترهای 1
1 | در پنجره Model Builder ، در قسمت Global Definitions روی Parameters 1 کلیک کنید . |
2 | در پنجره تنظیمات برای پارامترها ، بخش پارامترها را پیدا کنید . |
3 | در جدول تنظیمات زیر را وارد کنید: |
نام | اصطلاح | ارزش | شرح |
لامبدا | 1 | 1 | کش آمدن |
Q10 | 1[MPa] | 1E6 خب | پارامتر Mooney-Rivlin |
C01 | 1[MPa] | 1E6 خب | پارامتر Mooney-Rivlin |
متغیرهای 1
1 | در نوار ابزار صفحه اصلی ، روی |
رابطه فرضی بین کشش و تنش مهندسی را به عنوان یک عبارت متغیر بر حسب لامبدا و C10 و C01 هنوز ناشناخته تنظیم کنید .
2 | در پنجره تنظیمات برای متغیرها ، بخش متغیرها را پیدا کنید . |
3 | در جدول تنظیمات زیر را وارد کنید: |
نام | اصطلاح | واحد | شرح |
پ | 2*(C10+C01/لامبدا)*(لامبدا-1/لامبدا^2) | پا | استرس مهندسی |
اضافه کردن مطالعه
1 | در نوار ابزار Home ، روی |
2 | به پنجره Add Study بروید . |
3 | زیربخش مطالعات را پیدا کنید . در درخت انتخاب مطالعه ، Preset Studies for Selected Physics Interfaces>Stationary را انتخاب کنید . |
4 | روی Add Study در نوار ابزار پنجره کلیک کنید . |
5 | در نوار ابزار Home ، روی |
از یک مرحله مطالعه تخمین پارامتر برای تنظیم متغیرهای کنترل و انتخاب یک حل کننده بهینه سازی استفاده کنید. حل کننده Levenberg -Marquardt مخصوصاً برای مسائل حداقل مربعات مانند این کارآمد است.
مطالعه 1
تخمین پارامتر
1 | در نوار ابزار مطالعه ، روی |
2 | در پنجره تنظیمات برای تخمین پارامتر ، بخش داده های تجربی را پیدا کنید . |
3 | روی دکمه Browse کلیک کنید . از منو، Browse را انتخاب کنید . |
4 | به پوشه Application Libraries مدل بروید و روی فایل curve_fit_mooney_rivlin.csv دوبار کلیک کنید . |
5 | قسمت تنظیمات ستون را پیدا کنید . در جدول، برای انتخاب سلول در ردیف شماره 1 و ستون شماره 2 کلیک کنید. |
6 | در جدول تنظیمات زیر را وارد کنید: |
ستون ها | تایپ کنید | تنظیمات |
ستون 1 | پارامتر | نام = لامبدا |
ستون 2 | ارزش | بیان مدل=1، نام=col2، وزن=1 |
7 | از لیست نام ، لامبدا (کشش) را انتخاب کنید . |
8 | در قسمت متن واحد ، 1 را تایپ کنید . |
9 | در جدول، برای انتخاب سلول در ردیف شماره 2 و ستون شماره 3 کلیک کنید. |
10 | در قسمت متن عبارت Model ، P را تایپ کنید . |
11 | در قسمت متن Name ، engStress را تایپ کنید . |
12 | در قسمت متن واحد ، Pa را تایپ کنید . |
13 | قسمت Parameters را پیدا کنید . دوبار |
14 | در جدول تنظیمات زیر را وارد کنید: |
نام پارامتر | مقدار اولیه | مقیاس | کران پایین | کران بالا |
C01 (پارامتر Mooney-Rivlin) | 1[MPa] | 1[MPa] | ||
C10 (پارامتر Mooney-Rivlin) | 1[MPa] | 1[MPa] |
15 | قسمت Parameter Estimation Method را پیدا کنید . از لیست روش ، Levenberg-Marquardt را انتخاب کنید . |
16 | زیربخش تنظیمات Solver را پیدا کنید . از لیست روش حداقل مربعات زمان/پارامتر ، از حداقل مربعات هدف را انتخاب کنید . |
17 | در نوار ابزار مطالعه ، |
نتایج
نموداری از منحنی تنش-کرنش برازش حداقل مربعات را به همراه داده های اندازه گیری شده اضافه کنید.
تخمین پارامتر
1 | در نوار ابزار صفحه اصلی ، روی |
2 | در پنجره تنظیمات برای گروه طرح 1 بعدی ، تخمین پارامتر را در قسمت متن برچسب تایپ کنید . |
جهانی 1
1 | روی Parameter Estimation کلیک راست کرده و Global را انتخاب کنید . |
2 | در پنجره تنظیمات برای جهانی ، روی Replace Expression در گوشه سمت راست بالای بخش y-Axis Data کلیک کنید . از منو، تعاریف جهانی > متغیرها> P – استرس مهندسی – Pa را انتخاب کنید . |
3 | قسمت y-Axis Data را پیدا کنید . در جدول تنظیمات زیر را وارد کنید: |
اصطلاح | واحد | شرح |
P*lambda | پا | استرس واقعی (کوشی). |
P/lambda | پا | استرس دوم پیولا-کیرشهوف |
جهانی 2
1 | در پنجره Model Builder ، روی Parameter Estimation کلیک راست کرده و Global را انتخاب کنید . |
2 | در پنجره تنظیمات برای جهانی ، روی Add Expression در گوشه سمت راست بالای بخش y-Axis Data کلیک کنید . از منو، Solver>Parameter estimation>opt.glsobj.engStress.data – حداقل مربعات آزمایشی مقدار – Pa را انتخاب کنید . |
3 | برای گسترش بخش Coloring and Style کلیک کنید . زیربخش Line style را پیدا کنید . از لیست Line ، هیچکدام را انتخاب کنید . |
4 | زیربخش نشانگرهای خط را پیدا کنید . از لیست نشانگر ، دایره را انتخاب کنید . |
5 | در نوار ابزار تخمین پارامتر ، روی |
تخمین پارامتر
طرح را با تنظیم عنوان، برچسب های محور و موقعیت افسانه به پایان برسانید.
1 | در پنجره Model Builder ، روی Parameter Estimation کلیک کنید . |
2 | در پنجره تنظیمات برای گروه طرح 1 بعدی ، برای گسترش بخش عنوان کلیک کنید . |
3 | از لیست نوع عنوان ، هیچکدام را انتخاب کنید . |
4 | قسمت Plot Settings را پیدا کنید . |
5 | چک باکس x-axis label را انتخاب کنید . در قسمت متن مرتبط، Stretch را تایپ کنید . |
6 | کادر بررسی برچسب محور y را انتخاب کنید . در قسمت متن مرتبط، Stress را تایپ کنید . |
7 | قسمت Legend را پیدا کنید . از لیست موقعیت ، سمت چپ بالا را انتخاب کنید . |
گروه ارزشیابی 1
در نوار ابزار نتایج ، روی  Evaluation Group کلیک کنید .
Evaluation Group کلیک کنید .
تخمین پارامتر
ارزیابی جهانی 1
در پنجره Model Builder ، روی Evaluation Group 1 کلیک راست کرده و Global Evaluation را انتخاب کنید .
گروه ارزشیابی 1
1 | در پنجره تنظیمات برای گروه ارزیابی ، بخش داده را پیدا کنید . |
2 | از فهرست انتخاب پارامتر (لامبدا) ، Last را انتخاب کنید . |
ارزیابی جهانی 1
از گره ارزش هدف از پیش تعریف شده برای ارزیابی مقادیر تخمینی پارامترهای مواد C01 و C10 استفاده کنید .
1 | در پنجره Model Builder ، روی Global Evaluation 1 کلیک کنید . |
2 | در پنجره تنظیمات برای ارزیابی جهانی ، روی Add Expression در گوشه سمت راست بالای بخش عبارات کلیک کنید . از منو، Solver>Control Parameters>C10 – Mooney-Rivlin Parameter – Pa را انتخاب کنید . |
3 | روی Add Expression در گوشه سمت راست بالای بخش Expressions کلیک کنید . از منو، Solver>Control Parameters>C01 – Mooney-Rivlin Parameter – Pa را انتخاب کنید . |
4 | در نوار ابزار Evaluation Group 1 ، روی |




