هنگامی که یون ها در یک گاز بافر کمیاب تحت یک میدان الکتریکی ساکن قرار می گیرند، اثر ترکیبی نیروی الکتریکی و برخورد بین یون ها با مولکول های گاز محیطی باعث می شود که سرعت متوسط یون به یک مقدار تعادلی نزدیک شود که به عنوان سرعت رانش یون شناخته می شود. توانایی پیشبینی دقیق سرعت رانش برای عملکرد دستگاههایی مانند طیفسنجهای تحرک یونی، که قادر به تجزیه و تحلیل دقیق مخلوطهای گازی حاوی گونههای مختلف یونی با مرتبسازی گونههای مختلف بر اساس تغییرات کوچک در سرعت رانش آنها هستند، مهم است.
در این مثال، میانگین سرعت رانش گروهی از یونهای آرگون محاسبه شده و با دادههای تجربی مقایسه میشود. یونها با استفاده از رابط ردیابی ذرات شارژ شده مدلسازی میشوند. برخورد با گاز پسزمینه خنثی با استفاده از گره برخورد ، که از مدلهای برخورد تصادفی مختلف از جمله برخوردهای الاستیک و واکنشهای تبادل بار تشدید پشتیبانی میکند، اعمال میشود. میانگین سرعت رانش یون و دمای یون حاصل با مقادیر موجود در ادبیات مطابقت دارد.
در این مثال، ذرات مدل یونهای Ar+ هستند که در یک گاز پسزمینه خنثی از اتمهای Ar با دما و چگالی عددی مشخص آزاد میشوند. هدف تعیین میانگین سرعت حالت پایدار یا سرعت رانش یونها تحت تأثیر ترکیب نیروی الکتریکی پیوسته و برخوردهای گسسته با اتمهای خنثی در گاز پسزمینه است.
بخشهای زیر مروری بر تعریف نیروی الکتریکی و تئوری مدلسازی برخورد مونت کارلو با رابط ردیابی ذرات باردار ارائه میدهند. برای اطلاعات بیشتر در مورد نحوه مدلسازی برخوردهای تصادفی با ماژول ردیابی ذرات، به بخش نظریه برای رابط ردیابی ذرات باردار در راهنمای کاربران ماژول ردیابی ذرات مراجعه کنید .
این مدل از یک Sweep پارامتریک بر روی دامنه میدان الکتریکی برای تجزیه و تحلیل اثر آن بر سرعت رانش یون استفاده می کند. به جای اینکه مستقیماً مشخص شود، دامنه میدان الکتریکی بر حسب نسبت E / N در واحدهای تاونسند بیان میشود، که در آن E (واحد SI: V / m ) دامنه میدان الکتریکی و N (واحد SI: 1 / m) است. 3 ) چگالی عدد گاز پس زمینه است. واحد Townsend به صورت 1 Td = 10-21 V m2 تعریف می شود . در این مثال، Sweep پارامتریک از حداقل E / N = 500 Td تا حداکثر E / N = 10 5 Td اجرا می شود .
برای محدوده انرژی های در نظر گرفته شده در این مدل معیار، برهمکنش بین یون های Ar+ شبیه سازی شده و گاز پس زمینه کمیاب اتم های خنثی Ar تحت سلطه دو نوع واکنش زیر است:
1 |
2 |
برخورد بین یونهای آرگون و اتمهای خنثی در زمانهای تصادفی بر اساس فرکانس کل برخورد ν( t ) اتفاق میافتد (واحد SI: 1 / s ). توسط بیان ارائه شده است
که νj ( t ) فرکانس برخورد مرتبط با واکنش j ام در مدل است. در این مثال، j = 1 نشان دهنده برخورد الاستیک است در حالی که j = 2 نشان دهنده واکنش تبادل بار رزونانسی است .
سطح مقطع برخورد برای هر نوع واکنش می تواند تابعی دلخواه از سرعت نسبی باشد و معمولاً به صورت تجربی تعیین می شود. در این مثال، مقطع برخورد به عنوان تابعی از انرژی با استفاده از توابع تحلیلی تقریبی شده است ، اگرچه می توان آن را از جداول داده های وارد شده با نوع تابع درون یابی نیز درون یابی کرد .
گره Collision در واسط Charged Particle Tracing دو الگوریتم مجزا را برای تشخیص و اعمال برخوردهای تصادفی بین ذرات مدل و اتم ها یا مولکول ها در یک گاز پس زمینه کمیاب ارائه می دهد. انتخاب الگوریتم توسط لیست تشخیص برخورد کنترل میشود که دارای گزینههایی در گامهای زمانی برداشتهشده توسط حلکننده و روش برخورد صفر، تقریب گاز سرد است .
گزینه پیشفرض در گامهای زمانی که توسط حلکننده برداشته میشود ، یک رویکرد نیروی brute است که برخورد هر ذره مدل را در هر مرحله زمانی که توسط حلکننده برداشته میشود، بررسی میکند. مفروضات زیر مطرح می شود:
1 |
2 |
هر دو فرض 1 و 2 اندازه گام زمانی را که توسط حل کننده برداشته می شود برای معنی دار بودن نتایج محدود می کنند. اندازه گام باید به طور قابل توجهی کوچکتر از میانگین زمان آزاد بین برخوردها باشد، که اگر ذرات یون یا الکترون باشند که در معرض میدان الکتریکی قوی قرار می گیرند، ممکن است بسیار سریع افزایش یابد.
برای هر ذره، یک عدد تصادفی با توزیع یکنواخت U از بازه ( 0 ، 1 ) نمونه برداری می شود. سپس، از آنجایی که فرکانس برخورد در طول مرحله زمانی که توسط حلگر برداشته میشود ثابت فرض میشود، بیان منطقی برای وقوع یک برخورد با مقایسه U با احتمال معادله 3 به دست میآید .
در جایی که با ذکر این نکته که توابع توزیع احتمال U و 1 – U دقیقاً یکسان هستند، کمی سادهسازی شده است.
عدد شبه تصادفی U یک بار برای هر ذره در ابتدای هر مرحله زمانی که توسط حل کننده برداشته می شود نمونه برداری می شود.
روش برخورد تهی گزینه ، تقریب گاز سرد تلاشی است برای بهبود گزینه در مراحل انجام شده توسط حلگر با اجازه دادن به برخوردهای متعدد برای هر ذره در یک مرحله زمانی که حل کننده انجام می دهد و اجازه می دهد این برخوردها در زمان های متمایز بین رخ دهد. مراحل زمانی گسسته
این الگوریتم تشخیص برخورد فقط برای ذرات بسیار پرانرژی، آنهایی که با سرعت بسیار بالاتری نسبت به سرعت حرارتی گاز پس زمینه حرکت می کنند، کاربرد دارد.
این الگوریتم “روش برخورد تهی” نامیده می شود، زیرا رویکرد کلی این است که احتمال برخورد را در یک بازه زمانی معین بیش از حد تخمین بزنیم، برخوردها را بر اساس این تخمین بیش از حد فرکانس برخورد پیش بینی کنیم، و سپس کسری از برخوردها را بر اساس میزانی که تا چه حد است کنار بگذاریم. فرکانس واقعی کمتر از این مقدار ثابت مصنوعی است، با این فعل و انفعالات کنار گذاشته شده “برخورد تهی” نامیده می شود. فرکانس آزمایشی ν m را ثابت فرض کنید ، به طوری که ν m > ν( t ) در بازه زمانی ( 0 ، t ) باشد . اگر این فرکانس آزمایشی فرکانس برخورد واقعی در طول مرحله زمانی بود، پس معادله 3اعمال خواهد شد،
برای هر ذره مدل، یک زمان آزمایشی t m (واحد SI: s) محاسبه می شود به طوری که Pm ( t m ) = U 1 ، که در آن U 1 یک عدد توزیع یکنواخت در بازه ( 0 ، 1 ) است که به طور منحصر به فرد نمونه برداری می شود . برای هر ذره حل برای بازده زمان آزمایشی
اکنون که زمان آزمایش برای هر ذره محاسبه شده است، یک عدد تصادفی دوم توزیع یکنواخت U 2 ، که با U 1 همبستگی ندارد ، نیز به طور تصادفی از بازه ( 0 ، 1 ) برای هر ذره ای که در بازه زمانی دچار برخورد می شود، نمونه برداری می شود. ( 0 , t ) . اگر نابرابری
انتگرال اول در معادله 5 را می توان دقیقاً محاسبه کرد، زیرا فرکانس آزمایشی ثابت است، اما انتگرال دوم را فقط می توان به صورت عددی تقریب کرد زیرا فرکانس برخورد واقعی می تواند تابع دلخواه زمان باشد. بنابراین، اندازه گام زمانی که حلکننده برداشته است، همچنان بر دقت راهحل تأثیر دارد، حتی اگر این منبع خطا معمولاً به اندازه گزینه «گامهای زمانی که توسط حلکننده برداشته میشود» بزرگ نباشد .
برای هر یک از الگوریتمهای تشخیص برخورد، لازم است مشخص شود که برخورد شناسایی شده از نوع تبادل بار الاستیک یا رزونانسی است. احتمال وقوع p j یک نوع برخورد خاص است
دنباله حل کننده در این مثال از یک شرط توقف برای پایان دادن به مطالعه استفاده می کند، زمانی که ذرات متحمل تعداد کافی برخورد شده باشند. منطق پشت تعیین یک شرط توقف بر اساس حداکثر تعداد برخورد روی همه ذرات، این است که حداکثر زمان مورد نیاز برای سرعت متوسط یون برای رسیدن به حالت پایدار ممکن است با چندین مرتبه بزرگی در جاروب پارامتری دامنههای مختلف میدان الکتریکی متفاوت باشد. بنابراین، اجرای ساده شبیهسازی با حداکثر زمان حل یکسان برای هر مقدار پارامتر، یا برای مقادیر پارامترهایی که از نظر آماری سریعتر همگرا میشوند، بیهوده خواهد بود، یا برای آنهایی که از نظر آماری خیلی کند همگرا میشوند، نادرست است.
برای پیگیری تعداد کل برخوردهایی که هر ذره متحمل می شود، کادر بررسی Count collisions در تنظیمات گره Collisions انتخاب می شود . تعداد کل برخوردها روی همه ذرات مدل با استفاده از عبارت comp1.cpt.cptop1(comp1.cpt.col1.cex1.Nc) محاسبه میشود . در اینجا cpt.cptop1() یک جفت غیر محلی داخلی است که مجموع یک عبارت را روی تمام ذرات مدل محاسبه می کند.
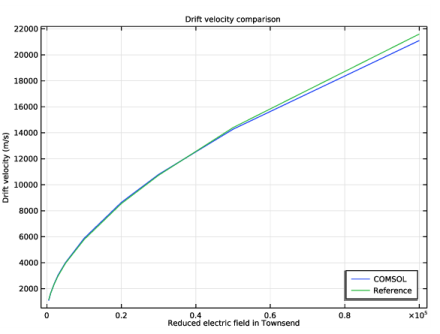
رابطه بین قدر میدان الکتریکی کاهش یافته و میانگین سرعت رانش یون در شکل 1 نشان داده شده است . دمای متوسط یون در شکل 2 نشان داده شده است .
شکل 1: نمودار سرعت رانش یونهای Ar+ در گاز پس زمینه آرگون خنثی. میانگین سرعت رانش با داده های تجربی مقایسه می شود.
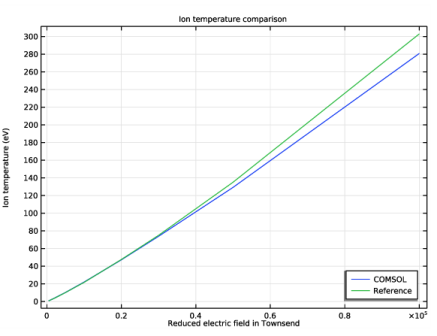
شکل 2: نمودار دمای یون یون های Ar+ در یک گاز پس زمینه از آرگون خنثی. میانگین دمای یون با داده های تجربی مقایسه می شود.
1. AV Phelps، “مقاطع و ضرایب ازدحام برای یون های نیتروژن و خنثی ها در N2 و یون های آرگون و خنثی ها در Ar برای انرژی هایی از 0.1eV تا 10keV”، J. Phys. شیمی. مرجع. داده ، جلد. 20، شماره 3، صص 557-573، 1991.
2. AV Phelps، “کاربرد مقاطع عرضی پراکندگی در مدل های شار یونی در غلاف های تخلیه”، J. Appl. فیزیک جلد 76، صص 747-753، 1994.
داده های خام را از Ref وارد کنید. 1 برای سرعت رانش یون به عنوان تابعی از میدان الکتریکی کاهش یافته برای برخوردهای الاستیک بین یون های Ar+ و اتم های خنثی Ar.
5 |
5 |
تقریب تحلیلی را برای مقطع تکانه برای پراکندگی الاستیک بین یونهای Ar+ و اتمهای خنثی Ar از Ref وارد کنید. 2 که به انرژی جنبشی ذرات بستگی دارد.
3 |
تقریب تحلیلی را برای برخورد همسانگرد الاستیک بین یونهای Ar+ و اتمهای خنثی Ar از Ref وارد کنید. 2 که به انرژی جنبشی ذرات بستگی دارد.
3 |
1 |
در پنجره Model Builder ، در قسمت Component 1 (comp1) روی Mesh 1 کلیک راست کرده و Build All را انتخاب کنید .
برای پیش بینی دقیق برخوردها، حداکثر زمان و اندازه گام زمانی دستی را مشخص کنید که متناسب با sqrt(maxCol/EoverN) است که به نوبه خود تقریباً با زمان آزاد بین برخوردها متناسب است.
2 |
7 |
شرط توقف را طوری تنظیم کنید که حلگر وابسته به زمان زمانی که به حداکثر تعداد برخوردها رسید، متوقف شود. مطمئن شوید که محلول را در مراحل زمانی قبل و بعد از تکمیل شرط توقف ذخیره کنید.
11 |
سرعت رانش را با داده های جدولی مقایسه کنید. این مقایسه را در آخرین مرحله زمانی انجام دهید، پس از اینکه سرعت رانش به مقدار تعادل رسید.
3 |
6 |
اکنون انرژی یون را با داده های جدول بندی شده مقایسه کنید. از Ref. 1 ، انرژی متوسط یون مربوط به توزیع انرژی یک بعدی است، یعنی E p = k B T /(2 e ) .
5 |