انفجار گاوسی گذرا
معرفی
این مثال مفاهیم مهمی را معرفی می کند که باید هنگام حل مسائل گذرا در ذهن داشته باشید. به طور خاص، رابطه بین محتوای فرکانس در منابع محرک مدل، وضوح مش و مرحله زمانی را بررسی می کند.
تعریف مدل
یک بیضی با دیوارهای سخت صدا این ویژگی جالب را دارد که یک سیگنال صوتی منتشر شده از یکی از کانون ها، ثانیه بعد در نقطه کانونی دیگر b / c دوباره فوکوس می کند، جایی که b (واحد SI: m) طول محور اصلی و c (SI) است. واحد: m/s) سرعت صوت است.
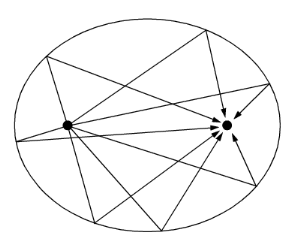
با الهام از Ref. 1 و رفر. 2 ، این مدل شامل یک انفجار گاوسی در یک کانون بیضی است تا برخی از خصوصیات مسائل صوتی وابسته به زمان را نشان دهد. طول محور اصلی و فرعی به ترتیب 10 متر و 8 متر است. محور اصلی با محور x منطبق است و کانون ها در x = – 3 متر و x = 3 متر قرار دارند. به دلیل تقارن، مدل را می توان به صفحه نیمه بالایی محدود کرد.
با نشان دادن چگالی سیال با ρ و سرعت صوت با c ، میدان فشار صوتی p ( x , t ) در داخل محفظه بیضوی توسط معادله موج اسکالر کنترل می شود.
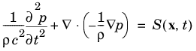
که در آن عبارت نقطه منبع در سمت راست با داده می شود
که در آن δ (2) تابع دلتای دیراک دو بعدی است. وابستگی زمانی انفجار توسط پالس گاوسی قطع تعیین می شود
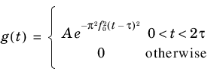
توصیف نرخ جریان هوا (واحد SI: m2 / s) دور از منبع، واقع در x = x 0 . پارامتر f 0 که متناسب با پهنای باند پالس است به صورت f 0 = 380 هرتز انتخاب می شود . همانطور که نمودارهای زیر نشان می دهد، با گرفتن τ = 1 / f 0 ، پالس بسیار نزدیک به یک گاوسی کامل می رسد، اثر دم های برش از نظر عددی ناچیز است.
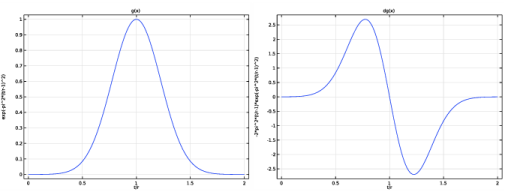
شکل 1: پالس گاوسی نرمال شده (چپ) و مشتق آن (راست).
یکی از ویژگیهای جالب تابع گاوسی این است که تبدیل فوریه آن، که در شکل 3 نشان داده شده است ، به همان اندازه ساده است (اثرات برش را نادیده بگیرید):

جایی که ω 0 = 2 π f 0 . بزرگی تبدیل فوریه برای افزایش فرکانس های زاویه ای ω به سرعت کاهش می یابد . عملاً تمام انرژی موجود در سیگنال در باند فرکانسی – 2 ω 0 < ω < 2 ω 0 با بیشتر آن بین -ω 0 و ω 0 متمرکز است .
بنابراین، هنگام استفاده از یک تابع اجباری از این نوع، کافی است طول موج های مربوط به فرکانس زاویه ای ω 0 را حل کنیم که به نوبه خود با فرکانس f 0 مطابقت دارد . در این مدل، پارامتری که حداکثر فرکانس برای تفکیک را تعریف میکند f max است ، برابر با 600 هرتز تنظیم شده است که کمی بالاتر از f 0 است (و پالس را کاملاً برطرف میکند).
به منظور تشخیص خوب پالس انتشار در فضا، قانون اصلی استفاده از حداقل 5 تا 6 عنصر در هر طول موج (در حداکثر فرکانس)، هنگام استفاده از عناصر لاگرانژ درجه دوم است. اندازه مش معمولی توسط
جایی که h max یک حداکثر اندازه مش-المان معمولی است و N تعداد عناصر در هر طول موج مورد نیاز برای حل یک موج هارمونیک با کمی دقت است. بحث زیر از N = 5 استفاده می کند . نکته مهم این است که در تجویز یک تابع اجباری که حاوی فرکانسهایی است که مش نمیتواند آنها را حل کند، سود کمی وجود دارد.
علاوه بر کنترل شکل پالس، وضوح مش محدودیتی را بر اندازه مراحل زمانی داخلی که توسط حل کننده برداشته می شود، اعمال می کند. در رابطهای گذرا ماژول آکوستیک، حلکننده از قسمت تنظیمات حلکننده گذرا که در سطح بالای فیزیک وجود دارد، کنترل میشود. کاربر باید حداکثر فرکانس را برای حل در مدل وارد کند. همچنین امکان انتخاب یک گام (روش) زمانی وجود دارد . در اینجا توصیه می شود از گزینه پیش فرض ثابت (ترجیح) استفاده کنید .
توضیح زمان گام
منطق انتخاب خودکار انجام شده به شرح زیر است. رابطه بین اندازه مش و اندازه گام زمانی ارتباط نزدیکی با عدد CFL دارد ( مراجعه 3 )، که به صورت تعریف می شود.
این عدد غیر بعدی را می توان به عنوان کسری از عنصری که موج در یک گام زمانی واحد طی می کند تفسیر کرد. اگر خطاهای گسسته به یک اندازه باشند ، یک عدد CFL در حدود 1 با وضوح یکسان در فضا و زمان مطابقت دارد. با این حال، معمولاً اینطور نیست.
به طور پیش فرض، COMSOL Multiphysics از روش ضمنی مرتبه دوم دقیق تعمیم یافته- α برای حل مسائل آکوستیک گذرا استفاده می کند. در فضا، پیش فرض عناصر لاگرانژ درجه دوم است. تعمیم یافته- α مقداری میرایی عددی فرکانس های بالا را معرفی می کند اما بسیار کمتر از روش BDF.
خطاهای گسسته زمانی برای α تعمیمیافته بزرگتر از خطاهای گسستهسازی مکانی هستند که عناصر مرتبه دوم در فضا استفاده میشوند. اندازه مرحله محدود کننده، که در آن خطاها تقریباً به یک اندازه هستند، در جایی در CFL < 0.2 یافت می شود . اگر اجبار از وضوح مش استفاده کامل نکند، میتوانید با یک مرحله زمانی طولانیتر کنار بیایید. یعنی اگر فرکانس های بالا از ابتدا وجود نداشته باشد.
هنگامی که تحریک شامل تمام فرکانسهایی است که مش میتواند حل کند، استفاده از کنترل خودکار مرحله زمانی که میتواند توسط حلکننده وابسته به زمان ارائه شود، فایدهای ندارد. زمانی که محتوای با فرکانس بالا ضعیف اما مهم وجود دارد، تنظیم تلرانس ها در کنترل خطای خودکار دشوار است. در عوض، می توانید از دانش خود در مورد اندازه مش معمولی، سرعت صدا و عدد CFL برای محاسبه و تجویز یک مرحله زمانی ثابت استفاده کنید. این دقیقاً رفتار پیش فرض زمانی است که روش ثابت (ترجیح) در قسمت تنظیمات حل گذرا انتخاب می شود . رایگان _گزینه مربوط به کنترل خودکار مرحله زمانی است، اما با برخی از کنترل های دقیق تر از گام های زمانی مجاز. این گزینه دوم هنوز توصیه نمی شود زیرا گزینه دستی معمولاً نتایج بسیار بهتری دارد (و سریعتر است).
مرحله زمانی داخلی ایجاد شده توسط گزینه ثابت (ترجیح) و حداکثر فرکانس وارد شده برای حل، با این فرض که کاربر شبکه ای ایجاد کرده است که به درستی همان فرکانس حداکثر (طول موج حداقل) را حل می کند، تنظیم می شود. مرحله زیر تولید می شود
با فرض اینکه N بین 5 و 6 باشد و عدد CFL تقریباً 0.1 باشد. این مقادیر حاشیه ایمنی خوبی به دست می دهند.
نتایج و بحث
استفاده از خواص هوا برای محیط و انتخاب چگالی مش بر اساس پارامترها. این مدل برای 0.035 ثانیه اجرا می شود تا بتوانید فوکوس مجدد را در نقطه فوکوس سمت راست تقریباً در 0.0315 ثانیه مطالعه کنید.
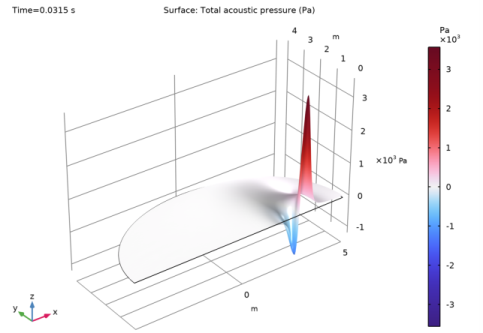
شکل 2: تمرکز مجدد تقریباً در 0.0315 ثانیه رخ می دهد. یک انیمیشن حس بهتری را به روند می دهد.
برای ترکیب انتخاب شده از اندازه مش، شکل پالس و مرحله زمانی، راه حل را می توان صاف و دقیق نشان داد. اگر عدد CFL به اندازه کافی کوچک باشد، انتخاب یک مقدار کوچکتر برای N منجر به نوسانات می شود (انتخاب یک فرکانس بسیار کم برای حل)، در حالی که انتخاب یک عدد CFL بالاتر (و در نتیجه یک گام زمانی بزرگتر) منجر به یک راه حل نادرست می شود.
شکل 3 تبدیل فوریه سیگنال منبع را نشان می دهد. رسم محتوای فرکانس سیگنال منبع راه خوبی برای انتخاب حداکثر فرکانس برای حل در مدل است.
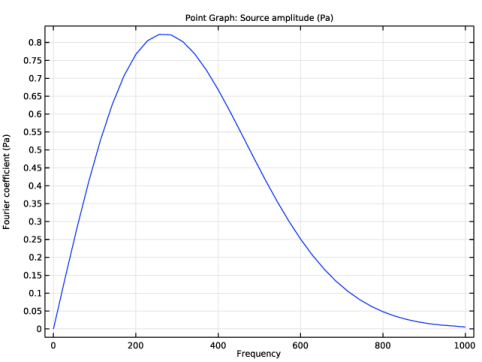
شکل 3: تبدیل فوریه سیگنال منبع.
منابع
Google Scholar Crossref، CAS 1. B. Yue و M. Guddati، “عناصر محدود کاهنده پراکندگی برای آکوستیک گذرا”، J. Acoust. Soc. صبح. ، جلد 118، شماره 4، صص Rev. 2132-2141.
2. H.-O. کریس، NA پترسون، و J. Yström، “تفاوت تقریب برای معادله موج مرتبه دوم”، SIAM J. از شماره. تجزیه و تحلیل ، جلد. 40، 1940-1967، 2002.
3. R. Courant, KO Friedrichs, and H. Lewy, “On the Partial Difference Equations of Mathematical Physics”, IBM Journal , vol. 11، صفحات 215-234، 1956.
مسیر کتابخانه برنامه: ماژول_آکوستیک/آموزش،_آکوستیک_فشار/ انفجار_گاوسی
دستورالعمل مدلسازی
از منوی File ، New را انتخاب کنید .
جدید
در پنجره جدید ، روی  Model Wizard کلیک کنید .
Model Wizard کلیک کنید .
مدل جادوگر
1 | در پنجره Model Wizard روی |
2 | در درخت Select Physics ، Acoustics>Pressure Acoustics>Pressure Acoustics, Transient (actd) را انتخاب کنید . |
3 | روی افزودن کلیک کنید . |
4 |
5 | در درخت انتخاب مطالعه ، General Studies>Time Dependent را انتخاب کنید . |
6 |
هندسه 1
بیضی 1 (e1)
1 | در نوار ابزار Geometry ، روی |
2 | در پنجره تنظیمات برای Ellipse ، بخش Size and Shape را پیدا کنید . |
3 | در قسمت متن a-semiaxis ، 5 را تایپ کنید . |
4 | در قسمت متن b-semiaxis ، 4 را تایپ کنید . |
5 | در قسمت نوشتار زاویه بخش ، 180 را تایپ کنید . |
نقطه 1 (pt1)
1 | در نوار ابزار هندسه ، روی |
2 | در پنجره تنظیمات برای Point ، بخش Point را پیدا کنید . |
3 | در قسمت متن x ، -3 را تایپ کنید . |
4 |
5 |
هندسه تکمیل شده باید مانند شکل زیر باشد.
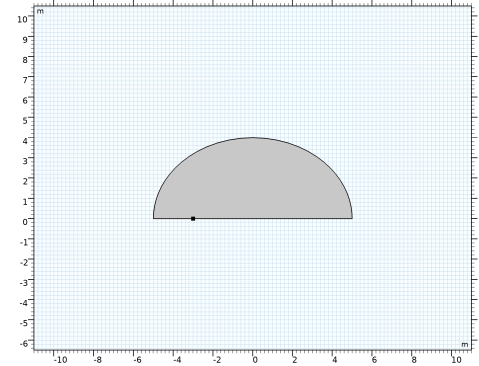
تعاریف جهانی
پارامترهای 1
1 | در پنجره Model Builder ، در قسمت Global Definitions روی Parameters 1 کلیک کنید . |
2 | در پنجره تنظیمات برای پارامترها ، بخش پارامترها را پیدا کنید . |
3 | در جدول تنظیمات زیر را وارد کنید: |
نام | اصطلاح | ارزش | شرح |
c_air | 343[m/s] | 343 متر بر ثانیه | سرعت صدا در هوا |
f_max | 600[Hz] | 600 هرتز | حداکثر فرکانس برای حل |
ن | 5 | 5 | عناصر در هر طول موج |
h_max | c_air/f_max/N | 0.11433 متر | اندازه عنصر معمولی |
آ | 4[m^2/s] | 4 متر مربع در ثانیه | دامنه منبع نقطه ای |
f0 | 380[Hz] | 380 هرتز | پهنای باند فرکانس منبع |
t0 | 1/f0 | 0.0026316 s | پالس منبع نصف عرض |
مواد را اضافه کنید
1 | در نوار ابزار Home ، روی |
2 | به پنجره Add Material بروید . |
3 | در درخت، Built-in>Air را انتخاب کنید . |
4 | روی Add to Component در نوار ابزار پنجره کلیک کنید . |
5 | در نوار ابزار Home ، روی |
آکوستیک فشار، گذرا (عملکرد)
حداکثر فرکانس قابل حل در مدل را وارد کنید. این مقدار را می توان از تحلیل فوریه منابعی که در شکل 3 نشان داده شده است، ارزیابی کرد .
در قسمت Transient Solver Settings حداکثر فرکانس را برای حل کردن وارد کنید و آن را روی f_max تنظیم کنید .
منبع نقطه 1
1 | در پنجره Model Builder ، در قسمت Component 1 (comp1) روی Pressure Acoustics, Transient (actd) کلیک راست کرده و Points>Point Source را انتخاب کنید . |
2 | فقط نقطه 2 را انتخاب کنید. |
3 | در پنجره تنظیمات برای منبع نقطه ، بخش منبع نقطه را پیدا کنید . |
4 | از لیست نوع ، پالس Gaussian را انتخاب کنید . |
5 | در قسمت متن A ، A را تایپ کنید . |
6 | در قسمت متنی f 0 ، f0 را تایپ کنید . |
7 | در قسمت متن t p ، t0 را تایپ کنید . |
مش
با استفاده از قابلیت مش کنترل شده توسط Physics، مش را ادامه داده و تولید کنید . فرکانس کنترل کننده حداکثر اندازه عنصر به صورت پیش فرض از مطالعه گرفته شده است . فرکانس های مورد نظر را در مرحله مطالعه تنظیم کنید . به طور کلی، 5 تا 6 عنصر درجه دوم در هر طول موج برای حل امواج مورد نیاز است. برای جزئیات بیشتر، مش بندی (رفع امواج) را در راهنمای کاربر ماژول آکوستیک ببینید . در این مدل از گزینه پیش فرض Automatic استفاده می کنیم که 5 عنصر در هر طول موج می دهد.
مطالعه 1
مرحله 1: وابسته به زمان
1 | در پنجره Model Builder ، در بخش مطالعه 1 ، روی Step 1: Time Dependent کلیک کنید . |
2 | در پنجره تنظیمات مربوط به زمان وابسته ، قسمت تنظیمات مطالعه را پیدا کنید . |
3 | در قسمت متنی زمان خروجی ، محدوده (0,0.5e-3,35e-3) را تایپ کنید . |
این تنظیم یک خروجی حل را در هر 0.5 میلی ثانیه از t = 0 تا t = 35 ms به شما می دهد. این نباید با مراحل زمانی که واقعاً توسط حل کننده برداشته شده اشتباه گرفته شود. اینها به طور خودکار بر اساس تنظیمات وارد شده در بالا تنظیم می شوند. برای اینکه ببینید در نهایت به کجا می رسند، موارد زیر را انجام دهید:
راه حل 1 (sol1)
1 | در نوار ابزار مطالعه ، روی |
2 | در پنجره Model Builder ، گره Solution 1 (sol1) را گسترش دهید ، سپس روی Time-Dependent Solver 1 کلیک کنید . |
3 | در پنجره تنظیمات برای حل وابسته به زمان ، برای گسترش بخش Time Steping کلیک کنید . |
حل کننده به طور خودکار تنظیمات وارد شده در سطح فیزیک (در بخش تنظیمات حل گذرا) را هنگامی که حل کننده پیش فرض تولید می شود یا هنگامی که برای اولین بار روی حل کلیک می شود، انتخاب می کند. به طور کلی نیازی به ویرایش این تنظیمات نیست.
کاربران با تجربه شاید ویرایش این تنظیمات را مفید بدانند.
مش 1
در پنجره Model Builder ، در قسمت Component 1 (comp1) روی Mesh 1 کلیک راست کرده و Build All را انتخاب کنید .
مطالعه 1
در نوار ابزار مطالعه ،  روی محاسبه کلیک کنید .
روی محاسبه کلیک کنید .
نتایج
فشار آکوستیک (عملکرد)

نمودار پیش فرض فشار را در زمان نهایی نشان می دهد. برای به دست آوردن یک طرح جذاب تر، می توانید یک ارتفاع اضافه کنید.
بیان قد 1
1 | در پنجره Model Builder ، گره فشار صوتی (actd) را گسترش دهید . |
2 | روی Surface 1 کلیک راست کرده و Height Expression را انتخاب کنید . |
میتوانید زمانهای مختلفی را برای نگاه کردن به موج با استفاده از گره اصلی فشار صوتی ( actd ) انتخاب کنید. در t = 0.0315 ثانیه، شما به لحظه ای نزدیک هستید که امواج دوباره فوکوس می کنند.
فشار آکوستیک (عملکرد)
1 | در پنجره Model Builder ، در بخش Results روی Acoustic Pressure (actd) کلیک کنید . |
2 | در پنجره Settings for 2D Plot Group ، بخش Data را پیدا کنید . |
3 | از لیست زمان (ها) ، 0.0315 را انتخاب کنید . |
4 | در نوار ابزار فشار صوتی (actd) ، روی |
5 |
نمودار حاصل در شکل 2 آمده است . متحرک کردن مسائل گذرا به طور کلی و انتشار موج به طور خاص گویا است. می توانید این کار را با کلیک راست بر روی گره Export و افزودن یک ویژگی Animation انجام دهید.
همچنین می توان با تعریف مجموعه داده آینه ای، میدان را در همه طرف منبع نقطه رسم کرد.
آینه 2 بعدی 1
1 | در نوار ابزار نتایج ، روی |
خط تقارن محور x است .
2 | در پنجره تنظیمات برای Mirror 2D ، بخش Axis Data را پیدا کنید . |
3 | از لیست روش ورود محور ، نقطه و جهت را انتخاب کنید . |
4 | زیربخش Direction را پیدا کنید . در قسمت متن X ، 1 را تایپ کنید . |
5 | در قسمت متن Y عدد 0 را تایپ کنید . |
فشار آکوستیک (عملکرد)
1 | در پنجره Model Builder ، در بخش Results روی Acoustic Pressure (actd) کلیک کنید . |
2 | در پنجره Settings for 2D Plot Group ، بخش Data را پیدا کنید . |
3 | از لیست Dataset ، Mirror 2D 1 را انتخاب کنید . |
4 | در نوار ابزار فشار صوتی (actd) ، روی |
5 |
6 | 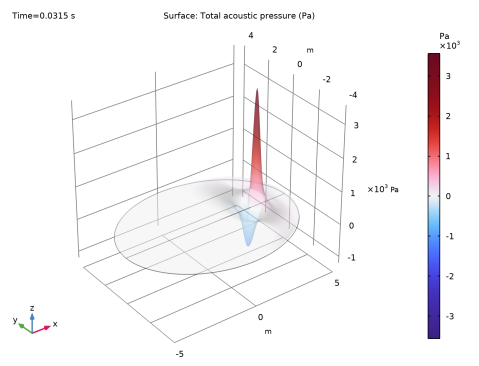 |
7 |
دستورالعمل های زیر نحوه ایجاد شکل 1 را نشان می دهد . این دستورالعمل ها اختیاری هستند.
با رسم دو تابع تحلیلی، گاوسی نرمال شده و مشتق آن را رسم کنید.
تعاریف جهانی
تحلیلی 1 (an1)
1 | در نوار ابزار Home ، روی |
2 | در پنجره تنظیمات برای تحلیل ، g را در قسمت متن نام تابع تایپ کنید . |
3 | قسمت Definition را پیدا کنید . در قسمت متن Expression ، exp(-pi^2*(x-1)^2) را تایپ کنید . |
4 | قسمت Plot Parameters را پیدا کنید . در جدول تنظیمات زیر را وارد کنید: |
بحث و جدل | حد پایین | حد بالا | واحد |
ایکس | 0 | 2 |
5 |
نتایج
گاوسی نرمال شده
1 | در پنجره تنظیمات برای گروه طرح 1 بعدی ، Normalized Gaussian را در قسمت متن برچسب تایپ کنید . |
2 | قسمت Plot Settings را پیدا کنید . |
3 | چک باکس x-axis label را انتخاب کنید . در قسمت متن مرتبط، t/r را تایپ کنید . |
4 | در قسمت متن برچسب محور y ، exp(-pi^2*(t/r-1)^2) را تایپ کنید . |
5 | در نوار ابزار Normalized Gaussian ، روی |
تعاریف جهانی
تحلیلی 2 (an2)
1 | در نوار ابزار Home ، روی |
2 | در پنجره تنظیمات برای تحلیل ، dg را در قسمت متن نام تابع تایپ کنید . |
3 | قسمت Definition را پیدا کنید . در قسمت متن Expression ، -2*pi^2*(x-1)*exp(-pi^2*(x-1)^2) را تایپ کنید . |
4 | قسمت Plot Parameters را پیدا کنید . در جدول تنظیمات زیر را وارد کنید: |
بحث و جدل | حد پایین | حد بالا | واحد |
ایکس | 0 | 2 |
5 |
نتایج
مشتق از هنجار. گاوسی
1 | در پنجره تنظیمات برای گروه طرح 1 بعدی ، مشتق از هنجار را تایپ کنید. گاوسی در قسمت نوشتار Label . |
2 | قسمت Plot Settings را پیدا کنید . |
3 | چک باکس x-axis label را انتخاب کنید . در قسمت متن مرتبط، t/r را تایپ کنید . |
4 | در قسمت نوشتاری برچسب محور y ، -2*pi^2*(t/r-1)*exp(-pi^2*(t/r-1)^2) را تایپ کنید . |
5 | در مشتق هنجار. نوار ابزار گاوسی ، |
در نهایت، نمودار نشان داده شده در شکل 3 را ایجاد کنید که در آن محتوای فرکانس منبع تحلیل شده است.
تبدیل فوریه منبع
1 | در نوار ابزار صفحه اصلی ، روی |
2 | در پنجره تنظیمات برای گروه طرح 1 بعدی ، تبدیل فوریه منبع منبع را در قسمت متن برچسب تایپ کنید . |
نمودار نقطه 1
1 | روی Fourier Transform of Source کلیک راست کرده و Point Graph را انتخاب کنید . |
2 | فقط نقطه 2 را انتخاب کنید. |
3 | در پنجره تنظیمات نمودار نقطهای ، روی Replace Expression در گوشه سمت راست بالای بخش y-Axis Data کلیک کنید . از منو، Component 1 (comp1)>Pressure Acoustics، Transient>Sources>actd.mls1.S – Source amplitude – N/m² را انتخاب کنید . |
4 | قسمت x-Axis Data را پیدا کنید . از لیست پارامتر ، تبدیل فوریه گسسته را انتخاب کنید . |
5 | از فهرست نمایش ، طیف فرکانس را انتخاب کنید . |
6 | از فهرست Scale ، Multiply by sampling period را انتخاب کنید . |
7 | در نوار ابزار تبدیل فوریه منبع ، روی |




