کابل زیردریایی 8 – جلوه های القایی 3 بعدی
معرفی
آموزشهای قبلی در این مجموعه – بهویژه آموزش جلوههای خازنی ، جلوههای القایی ، و جلوههای حرارتی – کابل را فقط بهصورت دو بعدی و ۲.۵ بعدی آنالیز کردهاند. اگرچه مدلهای دو بعدی ثابت کردهاند که یک ابزار مهندسی بسیار ارزشمند هستند، اما اساساً قادر به ثبت تعامل دقیق و پیچیده بین فازها، صفحهنمایش و زره نیستند. دلیل این امر این است که فازها و زره معمولاً با طول های مختلف و در جهت مخالف (برای دستیابی به پایداری پیچشی ) به هم می پیچند. همین پیچش مخالف، همراه با نسبت ابعاد بزرگ دستگاه، مدل سازی سه بعدی را به چالش تبدیل می کند.
در این میان، منابع محاسباتی به شدت افزایش یافته است. هنگام بررسی تحقیقات در مورد این موضوع [ 2 ، 7 ]، نمی توان متوجه ارتباط قوی بین سال انتشار و سطح جزئیات موجود در مدل های سه بعدی نشد. اگرچه حلکنندههای پیشرفته، پیکربندیهای مش پیچیده و قدرت محاسباتی برشی وضعیت را در طول سالها بسیار بهبود بخشیدهاند، بزرگترین تغییر عملکرد ناشی از معرفی دوره تناوب پیچخورده [ 2 ] و تناوب کوتاه پیچخورده [ 3 ] است: مدلسازی کابل سهبعدی با جزئیات کامل اکنون در عرض چند دقیقه با سخت افزار نسبتا ارزان امکان پذیر است.
این آخرین آموزش قصد دارد “پاسخ نهایی” را به مدل سازی سه بعدی کابل بدهد. این با بازخورد چندین متخصص در صنعت توسعه یافته است و با آخرین تحقیقات (2020) با در نظر گرفتن عملکرد و سطح جزئیات همتراز است . اعتبار سنجی گنجانده شده است: رفتار مدل ها در چارچوب refs تجزیه و تحلیل می شود. [ 1 ، 2 ، 4 ، 5 ، 6 ، و 7 ] و مشخصات رسمی کابل.
یادداشتی در مورد ارزش آموزشی
اگرچه این آموزش برای کسانی که در صنعت کابل کار می کنند کاربرد خاصی دارد، اما همه آن فقط «در مورد کابل» نیست. این آموزش – و کل مجموعه، برای آن موضوع – در مورد الکترومغناطیسی ، و آنالیز عددی است . این در مورد شیوه های مهندسی خوب، در مورد درک و به کارگیری نظریه، در مورد اعتبار سنجی نتایج، و در مورد ارائه نتایج خود به شیوه ای جذاب و آموزنده است.
کابل سه فاز با زره مغناطیسی و پیچ خورده وسیله ای ایده آل برای نشان دادن و بررسی پدیده های مختلف الکترومغناطیسی و عددی است. از آنجایی که بسیاری از این کابلها استاندارد شدهاند ، ویژگیهای فیزیکی آنها از متون موجود است (که اجازه اعتبارسنجی را میدهد ). در عین حال، آنها بخشی از تحقیقات در حال انجام هستند. این آنها را به ابزاری مناسب برای متخصصان صنعت و دانشجویان دانشگاهی تبدیل می کند تا به طور کلی با تجزیه و تحلیل عددی دستگاه های الکترومغناطیسی آشنا شوند.
تعریف مدل
هندسه سه بعدی همان کابل دو بعدی مورد استفاده در آموزش های قبلی را نشان می دهد ( شکل 1 را ببینید ). در آموزش Geometry & Mesh 3D تهیه و به تفصیل مورد بحث قرار گرفته است . جدا از سه بعدی بودن و پیچش، تفاوت اصلی این است که همه عایق ها با یک ماده “عایق عمومی” جایگزین شده اند (به بخش هادی ها و عایق ها مراجعه کنید ). جزئیاتی که باقی می مانند، یا ضروری هستند زیرا به شدت بر نتایج تأثیر می گذارند (معمولاً فلزات)، یا به این دلیل که به مش بندی و پس پردازش کمک می کنند. خواص مواد هادی ها مانند مواردی است که قبلاً استفاده می شد.

شکل 1: هندسه سه بعدی کابل، شامل سه فاز (زرد)، صفحه نمایش (قرمز)، XLPE (سفید) و زره (آبی).
توجه: اگر نظریه الکترومغناطیسی یا حساب برداری مورد شما نیست، نگران نباشید . فقط به بخش دستورالعمل های مدل سازی بروید و به آنجا خواهید رسید. با این حال، در بلندمدت، توصیه میشود برای درک عمیقتر نظریه زیربنایی سرمایهگذاری کنید. این به ویژه در هنگام عیب یابی و تفسیر نتیجه مفید خواهد بود.
مبانی نظری
این مدل قانون ماکسول آمپر را در حوزه فرکانس و به صورت سه بعدی با استفاده از پتانسیل بردار مغناطیسی A به عنوان یک متغیر وابسته حل می کند. تئوری درگیر با جزئیات کامل در بخش مبانی نظری آموزش اثرات استقرایی بررسی شده است . یک نسخه کوتاه شده در اینجا گنجانده شده است. هر دو متن از فرم دیفرانسیل همراه با سیستم واحد SI استفاده می کنند.
هنگام حل، هر چهار معادله ماکسول به طور مستقیم یا غیرمستقیم همراه با دو تعریف میدانی ( E و B بر حسب A ) و سه رابطه سازنده – آنهایی که حاوی خواص ماده ε ، σ ، و μ هستند، درگیر هستند :
قانون گاوس: | قانون فارادی: | |||
قانون گاوس مغناطیسی: | قانون ماکسول آمپر: | |||
میدان الکتریکی: | خواص دی الکتریک: | |||
خواص رسانا: | ||||
چگالی شار مغناطیسی: | خواص مغناطیسی: | |||
حفاظت از جریان
اجازه دهید با حفظ جریان شروع کنیم.  هنگامی که جریان ذخیره نمی شود، همانطور که در حوزه فرکانس ارائه شده است، شارژ زیادی دریافت می کنید . می توانید این قانون را با قانون گاوس ترکیب کنید تا یک قانون حفاظت فعلی اصلاح شده به دست آورید:
هنگامی که جریان ذخیره نمی شود، همانطور که در حوزه فرکانس ارائه شده است، شارژ زیادی دریافت می کنید . می توانید این قانون را با قانون گاوس ترکیب کنید تا یک قانون حفاظت فعلی اصلاح شده به دست آورید:
(1)
در اینجا، این اصطلاح به عنوان  چگالی جریان جابجایی شناخته می شود . همانطور که در آموزش اثرات خازنی اشاره شد ، چگالی جریان جابجایی در عایق ها برجسته است، چگالی جریان هدایت در هادی ها برجسته است و مجموع هر دو در همه زمان ها حفظ می شود. به همین دلیل است که برخی از کتابهای درسی جریان جابهجایی را در تعریف چگالی جریان گنجاندهاند:
چگالی جریان جابجایی شناخته می شود . همانطور که در آموزش اثرات خازنی اشاره شد ، چگالی جریان جابجایی در عایق ها برجسته است، چگالی جریان هدایت در هادی ها برجسته است و مجموع هر دو در همه زمان ها حفظ می شود. به همین دلیل است که برخی از کتابهای درسی جریان جابهجایی را در تعریف چگالی جریان گنجاندهاند:
(2)
قانون ماکسول آمپر اساساً بیان می کند که یک رابطه مستقیم بین میدان مغناطیسی H که یک هادی را احاطه کرده و چگالی جریانی  که از آن عبور می کند وجود دارد . اگر تفاوت آن را در نظر بگیرید ، به چیزی بسیار راحت منجر می شود:
که از آن عبور می کند وجود دارد . اگر تفاوت آن را در نظر بگیرید ، به چیزی بسیار راحت منجر می شود:
(3)
این طبق تعریف درست است: از حساب بردار پایه چنین برمیآید که واگرایی کرل هر میدان برداری همیشه باید صفر باشد. به عبارت دیگر، اگر چگالی جریان را برابر با کرل H تعریف کنید ، یک قانون بقای فعلی را به صورت رایگان دریافت میکنید – هیچ معادله اضافی برای اجرای آن لازم نیست.
پتانسیل بردار مغناطیسی
قانون گاوس و قانون ماکسول آمپر اکنون به کار گرفته شده اند. اگر سومین رابطه سازنده 3 را اضافه کنید ;  ، در نهایت با موارد زیر مواجه می شوید:
، در نهایت با موارد زیر مواجه می شوید:
(4)
اکنون یک میدان برداری A را در نظر بگیرید ، پتانسیل بردار مغناطیسی بر حسب Vs/m (یا Wb/m)، که حلقه آن برابر با چگالی شار مغناطیسی B انتخاب شده است . به این معنا که؛  . پتانسیل بردار مغناطیسی یک میدان قابل اندازه گیری مستقیم یا چیزی نیست و همچنین منحصر به فرد نیست. بدون هیچ گونه محدودیت اضافی، بسیاری از فیلدهای مختلف A وجود دارد که الزام 4
. پتانسیل بردار مغناطیسی یک میدان قابل اندازه گیری مستقیم یا چیزی نیست و همچنین منحصر به فرد نیست. بدون هیچ گونه محدودیت اضافی، بسیاری از فیلدهای مختلف A وجود دارد که الزام 4  را برآورده می کند . با استفاده از این رابطه بین A و B ، و یک بار دیگر واگرایی را در نظر بگیرید، دریافت می کنید:
را برآورده می کند . با استفاده از این رابطه بین A و B ، و یک بار دیگر واگرایی را در نظر بگیرید، دریافت می کنید:
(5)
بنابراین اگر B را بر اساس A تعریف کنید ، بقای شار مغناطیسی (قانون گاوس برای مغناطیس) را به صورت رایگان دریافت خواهید کرد. این دقیقاً به همان دلیلی است که شما حفاظت فعلی را به صورت رایگان دریافت کردید. اگر اکنون این تعریف B را در معادله القای الکترومغناطیسی ماکسول-فارادی جایگزین کنید، دریافت خواهید کرد:
(6)
این آخرین قطعه از پازل 5 را به شما می دهد :  . حال، B و E هر دو را می توان بر حسب A بیان کرد . اگر این نتیجه را در معادله 4 جایگزین کنید ، خواهید دید:
. حال، B و E هر دو را می توان بر حسب A بیان کرد . اگر این نتیجه را در معادله 4 جایگزین کنید ، خواهید دید:
(7)
در نهایت، اگر چند عبارت را عوض کنید و همه چیز را در سمت چپ قرار دهید، معادله دیفرانسیل جزئی سه بعدی زیر را برای متغیر وابسته A دریافت خواهید کرد :
(8)
به دلیل پیچش مضاعف، این معادله به عنوان یک معادله نوع کرل شناخته می شود. رابط میدان های مغناطیسی از این معادله در دامنه ها برای تعیین مقدار A و در نتیجه مقدار تمام فیلدهای مشتق شده از آن استفاده می کند: E ، D ، J ، B و H.
برای مرزهای بیرونی از شرط پیش فرض  استفاده می شود که A را در جهت سطح نرمال محدود می کند. بنابراین، B عمود بر سطح نرمال خواهد بود. خطوط شار مغناطیسی در امتداد سطح جریان خواهند داشت. این به عنوان یک وضعیت عایق مغناطیسی (در قیاس با عایق الکتریکی یا حرارتی) شناخته می شود. همراه با معادله دیفرانسیل جزئی، شرط مرزی مجموعه کاملی از معادلات را به شما می دهد.
استفاده می شود که A را در جهت سطح نرمال محدود می کند. بنابراین، B عمود بر سطح نرمال خواهد بود. خطوط شار مغناطیسی در امتداد سطح جریان خواهند داشت. این به عنوان یک وضعیت عایق مغناطیسی (در قیاس با عایق الکتریکی یا حرارتی) شناخته می شود. همراه با معادله دیفرانسیل جزئی، شرط مرزی مجموعه کاملی از معادلات را به شما می دهد.
به منظور تحریک سیستم، یک میدان الکتریکی خارجی E ext در هادی های اصلی کابل اعمال می شود (برای اطلاعات بیشتر در این مورد، بخش دستورالعمل های مدل سازی را ببینید ). این میدان از یک منبع خارجی می آید که در مدل گنجانده نشده است، احتمالاً یک نیروگاه یا یک مزرعه بادی.
توابع شکل و ترتیب گسسته سازی
برای حل عددی معادله دیفرانسیل جزئی مانند معادله 8 (بر خلاف تحلیلی)، فضا باید به تعداد محدودی از عناصر تقسیم شود – از این رو اصطلاح، روش اجزای محدود (FEM) نامیده می شود. برای این، یک مش ساخته شده است. هر عنصر مش با یک تابع شکل به اصطلاح مرتبط است . سپس راه حل واقعی بر روی این توابع شکل پیش بینی می شود تا سیستمی از معادلات با تعداد محدود مجهول یا درجه آزادی (DOFs) ایجاد شود.
جزئیات این روش خارج از محدوده این آموزش است . در حال حاضر، کافی است توابع شکل را پیکسل های تصویر دیجیتال خود در نظر بگیرید. حل مدل به معنای یافتن مقادیر RGB پیکسل های شماست، به طوری که تصویر به بهترین شکل ممکن به تصویر آنالوگ واقعی نزدیک شود. تصویر آنالوگ واقعی چگونه به نظر می رسد، با معادله دیفرانسیل جزئی توصیف می شود.
پیکسل ها در تصاویر دیجیتال معمولاً یک رنگ دارند. با این حال، توابع شکل می توانند ثابت باشند، می توانند شیب خطی (عناصر مرتبه اول)، سهمی (عناصر مرتبه دوم) یا حتی مرتبه بالاتر باشند. عناصر مرتبه دوم میتوانند شکل واقعی را با جزئیات بیشتری نسبت به عناصر خطی توصیف کنند – دقیقاً مانند یک چند جملهای مرتبه بالاتر در برازش با مجموعه داده اندازهگیری شده بهتر است . با این حال، عناصر خطی بسیار ناچیزتر هستند. آنها راه حل را با دقت کمتری توصیف می کنند، اما پایدارتر هستند و درجات آزادی کمتری دارند.
برای مدل های دوبعدی، منابع محاسباتی به ندرت مشکل ساز هستند. همه مدلهای دوبعدی این سری از یک مش استاندارد معمولی با عناصر درجه دوم استفاده میکنند. با این حال، برای مدلهای سهبعدی بزرگ – بهویژه زمانی که حلکنندههای مستقیم، مشهای پیچیده و مواد غیرخطی درگیر هستند – ویژگیهای ناب و پایدار عناصر درجه اول از اهمیت حیاتی برخوردار است. هزینه ای که پرداخت می کنید جزئیات کمتری است، اما چیزی که به دست می آورید کاهش شدید مصرف حافظه و تلاش محاسباتی کلی است.
در مورد ثبات عددی
هادی ها و عایق ها
رسانایی الکتریکی احتمالاً خاصیت ماده ای با بیشترین دامنه مقادیر طبیعی است (یعنی حتی ابررسانایی را در نظر نمی گیریم ). پلی اتیلن متقاطع (XLPE) در کابل دارای رسانایی الکتریکی با مقداری در حدود 1 · 10-18 S /m است ، در حالی که مس دارای مقدار 6 · 10 7 S / m – کنتراست 6 · 10 25 است. . برای یک مدل اجزای محدود، کنتراست 1 · 10 6 در حال حاضر نزدیک به آن چیزی است که دقت عددی سیستم می تواند انجام دهد.
به عبارت دیگر، اگر دستگاهی عمدتاً القایی (یا مقاومتی) باشد و رساناها به طور کامل محلول را تعیین کنند، هر ماده ای با رسانایی چندین مرتبه کمتر از آن را می توان «عایق» در نظر گرفت. به همین ترتیب، اگر دستگاهی عمدتاً ماهیت خازنی داشته باشد، این عایق ها هستند که محلول را تعیین می کنند و هر ماده ای با رسانایی بالاتر از 1 S/m می تواند به عنوان “رسانا” در نظر گرفته شود (به آموزش جلوه های خازنی مراجعه کنید ). گرفتن دقیق هر دو اثر خازنی و مقاومتی در یک مدل به طور همزمان اغلب غیر ضروری است و ممکن است به دقت عددی بسیار بالایی نیاز داشته باشد.
مسلماً، در فرکانسهای بالاتر این موضوع کمتر میشود، زیرا جریانهای جابهجایی نقش جریانهای رسانش را در عایقها به عهده میگیرند (یعنی معادله 1 همچنان قابل حل خواهد بود). به عنوان مثال، در فرکانس 50 هرتز ، “رسانایی کل” XLPE را می توان در نظر گرفت که  دارای یک هنجار
دارای یک هنجار  S/m است . این در حال حاضر 9 مرتبه بزرگتر از رسانایی الکتریکی به تنهایی است.
S/m است . این در حال حاضر 9 مرتبه بزرگتر از رسانایی الکتریکی به تنهایی است.
استفاده از رسانایی تثبیت کننده
ناتوانی سیستم عددی در حل کنتراست ماده بسیار بزرگتر از 1 · 10 6 توضیح می دهد که چرا بسیاری از مدل های الکترواستاتیک فلزات را حوزه های هم پتانسیل در نظر می گیرند. همچنین توضیح می دهد که چرا این مدل کابل پیچ خورده سه بعدی با 50 S/m به عنوان تنظیم رسانایی برای “عایق عمومی” به خوبی کار می کند. در واقع باید مقدار قابل توجهی غیر صفر در مقره ها داشته باشد. در غیر این صورت مدل تکی می شود.
دلیل این امر را می توان در معادله 8 مشاهده کرد . هنگامی که رسانایی خیلی کوچک باشد، عبارت هلمهولتز از نظر عددی ناچیز می شود (با توجه به دقت عددی استفاده شده از صفر قابل تشخیص نیست). این معادله را به:
از نظر عددی ناچیز می شود (با توجه به دقت عددی استفاده شده از صفر قابل تشخیص نیست). این معادله را به:
(9)
که به عنوان تقریب مغناطیسی نیز شناخته می شود ، یعنی; تمام مشتقات زمانی مرتبه اول و دوم از سیستم معادلات حذف شده اند. مشکل این است که اندازه گیری نشده است (همانطور که به طور خلاصه در بخش مبانی نظری به آن اشاره شد ). به عبارت دیگر، معادله 9 اطلاعات کافی برای یافتن یک راه حل منحصر به فرد برای پتانسیل بردار مغناطیسی A در اختیار شما قرار نمی دهد – می توانید آن را با یک معادله خطی که فقط مشتقات آن را می دانید مقایسه کنید . برای یک حل کننده مستقیم، این یک مشکل است.
راه های زیادی برای حل این مشکل وجود دارد، از جمله انواع مختلف Gauge Fixing ، ترکیبی از فرمول های مختلف 7 (AV-formulation، AV m -formulation)، یا استفاده از حل کننده های تکراری تخصصی. با این حال، یکی از ساده ترین و موثرترین ترفندها در مهندسی عددی، دادن رسانایی تثبیت کننده به عایق ها است که به اندازه کافی بزرگ باشد تا مدل را از نظر عددی ثابت نگه دارد، در عین حال به اندازه کافی کوچک باشد که تأثیر قابل توجهی روی محلول نداشته باشد.
توجه: برای دستگاههای القایی در حوزه فرکانس، میتوانید از عمق پوست  برای قضاوت در مورد بزرگ یا کوچک بودن σ استفاده کنید. هنگامی که عمق پوست چندین مرتبه بزرگتر از بعد مورد نظر باشد، σ احتمالاً تأثیر قابل توجهی بر محلول نخواهد داشت. برای عایق های با S/m 50 عمق پوست به حدود 10 متر می رسد . بسیار بزرگتر از ویژگی های مقطع کابل.
برای قضاوت در مورد بزرگ یا کوچک بودن σ استفاده کنید. هنگامی که عمق پوست چندین مرتبه بزرگتر از بعد مورد نظر باشد، σ احتمالاً تأثیر قابل توجهی بر محلول نخواهد داشت. برای عایق های با S/m 50 عمق پوست به حدود 10 متر می رسد . بسیار بزرگتر از ویژگی های مقطع کابل.
در نهایت، توجه داشته باشید که این موضوع برای مدلهای دو بعدی مطرح نیست، زیرا همراه با شرایط مرزی پیشفرض عایق مغناطیسی ، وادار کردن پتانسیل بردار مغناطیسی A به خارج از صفحه برای به دست آوردن یک راهحل منحصر به فرد کافی است (همانطور که در Inductive مشاهده میشود. آموزش افکت ها ).
تثبیت جبرانی
بخش چهارم این آموزش – بخش دستورالعملهای مدلسازی – تثبیت جبرانشده – یک رویکرد تجربی را مورد بحث قرار میدهد که مدل را تثبیت میکند و متعاقباً یک اصطلاح جبرانی اضافه میکند که اثرات تثبیت را کاهش میدهد.
نسبت دادن 50 S/m به عایق هایی مانند هوا یا پلی اتیلن، بسیار شبیه افزودن یک عبارت غیر فیزیکی اضافی به معادله 8 است :
(10)
سپس این معادله یک بار حل می شود. “حل” به این معنی است که در این مورد، معکوس ماتریس (یا فاکتورگیری LU آن، حداقل) توسط حل کننده مستقیم تعیین می شود. سپس از عوامل LU برای تعیین A استفاده می شود . این روشی است که معمولاً مدل را حل می کنید.
در چندین مورد در این مجموعه آموزشی، چگالی جریان خارجی J e به عنوان یک عبارت کمککننده ارائه میشود، و میتوانید آن را در سمت راست معادله 10 در نظر بگیرید – توجه داشته باشید که همه عبارتهای این معادله نشان دهنده نوعی جاری . افزودن یک عبارت کمک کننده به سمت راست بر معکوس ماتریس تأثیری نخواهد داشت. با تنظیم  ، به موارد زیر خواهید رسید:
، به موارد زیر خواهید رسید:
(11)
اگر بار دوم را با استفاده از همان فاکتورسازی LU حل کنید (که فقط باید کسری از زمان اولیه را ببرد)، اصطلاحات مصنوعی در سمت چپ و راست حذف خواهند شد و مقدار جدیدی پیدا خواهید کرد. برای پتانسیل بردار مغناطیسی:  . مقداری که معادله اصلی، معادله 8 را برآورده می کند .
. مقداری که معادله اصلی، معادله 8 را برآورده می کند .
نگاهی به آن از منظر مهندسی؛ شما ابتدا یک رسانایی محدود در عایق های خود وارد می کنید که باعث نشت جریان  از یک هادی به هادی دیگر می شود. سپس مقدار نشتی را ارزیابی کرده و پمپی را در مقره ها نصب می کنید که همان مقدار جریان را در جهت مخالف پمپ می کند و بر توزیع چگالی جریان در عایق ها و هادی ها تأثیر می گذارد.
از یک هادی به هادی دیگر می شود. سپس مقدار نشتی را ارزیابی کرده و پمپی را در مقره ها نصب می کنید که همان مقدار جریان را در جهت مخالف پمپ می کند و بر توزیع چگالی جریان در عایق ها و هادی ها تأثیر می گذارد.
با این حال، لغو کامل نخواهد بود 8 ، و دقت میدان های الکتریکی در مقره ها ممکن است تحت تأثیر قرار گیرد. زمانی که کنتراست در خواص مواد فقط متوسط باشد، نباید از این روش استفاده کرد. با این حال، در این موارد، ثبات عددی معمولاً در وهله اول یک مسئله نیست.
رویکرد مدلسازی
دستورالعمل های مدل سازی در این آموزش در پنج بخش (همانطور که در زیر ذکر شده است) تقسیم شده است و برای هر بخش یک فایل مرجع ذخیره شده است. این به شما این امکان را می دهد که از جایی در نیمه راه آموزش شروع کنید ( اگرچه گذراندن آن از ابتدا تا انتها توصیه می شود ).
مدل 2 بعدی اکسترود شده
هدف اولیه فقط به دست آوردن یک مدل عملکردی به صورت سه بعدی و به دست آوردن نوعی تخمین از دقت است. برای این منظور، توالی هندسه کاملاً پارامتری شده در حالتی قرار می گیرد که اساساً چیزی بیش از یک اکستروژن ساده از یک هندسه دو بعدی نیست. در این حالت، هندسه سه بعدی باید بتواند نتایج به دست آمده از دو بعدی را به خوبی بازتولید کند. به این معنا که؛ البته اگر سطح جزئیات یکسانی داشت، و اگر از مش یکسانی استفاده می کرد، با همان ترتیب گسسته سازی .
مقایسه مدل دوبعدی اکسترود شده با پیکربندی دوبعدی کاملاً دقیق که در آموزش جلوههای القایی مورد بحث قرار گرفته است، اساساً به شما این امکان را میدهد که آسیبهای ناشی از امتیازاتی را که باید میدادید تا مشکل را در سهبعدی قابل کنترل نگه دارید، ارزیابی کنید. اتفاقاً برعکس نیز صدق میکند: متوجه خواهید شد که مدل سهبعدی با توجه به حذف تمام آن جزئیات به طرز شگفتآوری دقیق است. موضوع دقت و ارتباط برخی جزئیات قبلاً چندین بار مورد بحث قرار گرفته است، به ویژه در آموزش های خازنی ، القایی و اثرات حرارتی .
مدل پیچش سه بعدی
پس از اینکه مدل در حالت دوبعدی اکسترود شده خود آزمایش شد، به حالت چرخشی کامل سه بعدی با شرایط تناوبی پیچ خورده تبدیل می شود (به بخش تناوب پیچ خورده مراجعه کنید ) . این به شما این امکان را می دهد که تأثیر پیچش را بر روی شار مغناطیسی، جریان و چگالی تلفات در فازها، صفحه نمایش ها و زره ها بررسی کنید. علاوه بر این، به شما امکان می دهد با مدل های 2 بعدی و 2.5 بعدی (در دمای اتاق) مقایسه کنید. می توانید با استفاده از منابعی مانند مرجع [ 2 ] مقایسه خود را بیشتر تأیید کنید.
مقاومت خطی سه بعدی
از آنجایی که این نوع کابل معمولاً در دماهای حدود 80 تا 90 درجه سانتیگراد کار می کند ، خواص مواد هادی ها معمولاً شامل یک اصلاح دما به شکل مقاومت خطی شده 9 است :
(12)
که ρ 0 به مقاومت مرجع در T ref اشاره دارد و α ضریب دمای مقاومت در 1/K است . مدلهای مورد بحث در اینجا واقعاً برای T حل نمیشوند . در عوض، خوانش دما از مدل گرمایش القایی کاملا جفت شده ارائه شده در آموزش اثرات حرارتی گرفته شده است . با خواص مواد اصلاح شده، نتایج یک بار دیگر تجزیه و تحلیل می شوند.
تثبیت جبرانی
علاوه بر این، اجرای تثبیت جبران شده – همانطور که در بخش تثبیت جبران شده توضیح داده شد – نشان داده شده است، و تاثیر نشت جریان بین سیم های زره بر روی راه حل کلی بررسی می شود.
پیکربندی کوتاه دوره ای
در نهایت، هندسه و مش اصلاح میشوند تا نوع متفاوتی از تناوب را ایجاد کنند، و اندازه مدل را صد برابر میکند و در عین حال دقت مشابهی را ارائه میدهد (به بخش تناوب کوتاه پیچ خورده مراجعه کنید ). نتایج با مدل تمام دوره ای مقایسه شده است.
روی LAY LENGTH و CROSS PITCH
پیچش بُعد جدیدی به دستگاه میافزاید، ابعادی که مدلهای دوبعدی نمیتوانند آن را ثبت کنند. فاصله مورد نیاز برای تکمیل یک دور کامل فازها حول محور کابل، طول بستر فاز یا L pha نامیده می شود ، شکل 2 را ببینید . در مورد زره نیز استدلال مشابهی وجود دارد. طول لایه معمولاً بر حسب فاز و قطر زره بیان می شود. برای مدل های این آموزش، ما داریم:
(13)
که در آن D pha قطر بیرونی هر سه فاز و صفحه های ترکیبی است و بازوی D قطر مرکزی حلقه سیم زره است. علامت منفی منعکس کننده جهت مخالف چرخش زره است.
سپس مقدار پیچش فاز و زره بر حسب درجه بر متر طول کابل به صورت زیر محاسبه می شود:
(14)
و اختلاف زاویه پیچش بین فازها و زره با  درجه بر متر افزایش می یابد. مقدار مترهایی که این اختلاف برای آنها 360 درجه می شود ، همان چیزی است که مورد توجه است. این طولی است که زره برای ایجاد یک انقلاب کامل در فازها لازم است. در آن نقطه، همان سیم زره دوباره با همان فاز برخورد میکند و الگوی خود را تکرار میکند (البته در یک زاویه متفاوت، شکل 3 را ببینید ). این طول را گام متقاطع کابل می نامند :
درجه بر متر افزایش می یابد. مقدار مترهایی که این اختلاف برای آنها 360 درجه می شود ، همان چیزی است که مورد توجه است. این طولی است که زره برای ایجاد یک انقلاب کامل در فازها لازم است. در آن نقطه، همان سیم زره دوباره با همان فاز برخورد میکند و الگوی خود را تکرار میکند (البته در یک زاویه متفاوت، شکل 3 را ببینید ). این طول را گام متقاطع کابل می نامند :
(15)
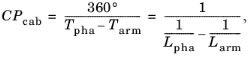
جایی که درجه ها لغو می شوند. مدلهای پیچش سهبعدی طولانی ساختهشده در این آموزش، طولی برابر با یک برابر زمین متقاطع کابل دارند (اگرچه دورههای متعدد پشتیبانی میشوند).
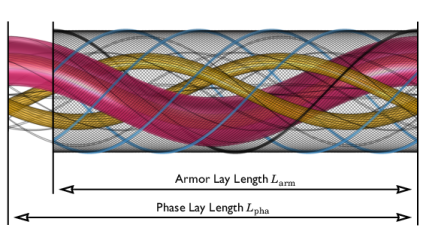
شکل 2: طول لایه زره کابل و طول لایه لایه (تصویر با ضریب 5 در جهت طولی مقیاس شده است). طول لایی فاصله ای است که برای مارپیچ ها لازم است تا یک دور کامل را کامل کنند.
تناوب پیچ خورده
این آموزش از یک شرط تناوب پیچ خورده استفاده می کند که پتانسیل بردار مغناطیسی را محدود می کند:  . هنگام اعمال این محدودیت، بهطور پیشفرض، یک تبدیل مختصات «مستقیم» ساده انجام میشود، بر اساس مکان و جهت صفحات مبدا و مقصد (برای مثال، صفحاتی را در نظر بگیرید که نسبت به یکدیگر کج هستند، همانطور که برای تقارن بخش وجود دارد . ).
. هنگام اعمال این محدودیت، بهطور پیشفرض، یک تبدیل مختصات «مستقیم» ساده انجام میشود، بر اساس مکان و جهت صفحات مبدا و مقصد (برای مثال، صفحاتی را در نظر بگیرید که نسبت به یکدیگر کج هستند، همانطور که برای تقارن بخش وجود دارد . ).
برای بسیاری از موارد، این راه حل خارج از جعبه کار می کند. با این حال، چرخش به ورودی های کاربر بیشتری نیاز دارد، زیرا صفحات تقارن دایره ای هستند و از آنجایی که “عدم تطابق” ممکن است عمدی بوده باشد – در نهایت، COMSOL از هر نوع هندسه پشتیبانی می کند، نه فقط از هندسه ها . جهت صفحه تناوب با توجه به سیستم مختصات جهانی با پیشروی در امتداد کابل تغییر می کند ( شکل 3 و مراجع [ 2 ، 3 ] را ببینید). پس از طی مسافتی از کابین CP ، حول محور کابل، با زاویه پیچش:
(16)
ممکن است متوجه شده باشید که، اگرچه این عبارت بر اساس L pha است ، اما طول قرار گرفتن زره به همان اندازه کار خواهد کرد: اگر زاویه پیچش را با استفاده از بازوی L محاسبه کنید ، مقدار منفی خواهد بود و تفاوت بین این دو خواهد بود. یک انقلاب کامل
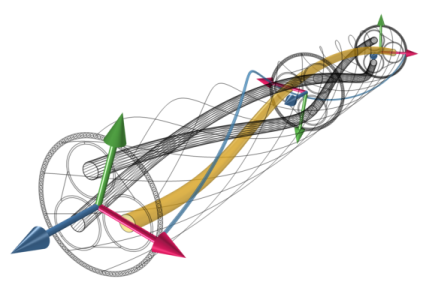
شکل 3: جهت صفحه تناوب با پیشروی در امتداد کابل تغییر می کند.
توجه: برای اینکه تناوب پیچ خورده به درستی کار کند، مهم است که گره های مش روی مرزهای مبدا و مقصد مطابقت داشته باشند. این به این دلیل است که مدل از فرمول پتانسیل برداری با عناصر curl به صورت سه بعدی استفاده می کند. با یک مش غیر منطبق، پتانسیل بردار مغناطیسی باید درون یابی شود، که باعث می شود دقت و پایداری مدل شما کاهش یابد. اقداماتی که می توانید انجام دهید تا اطمینان حاصل شود که مش از کیفیت خوبی برخوردار است، در آموزش هندسه و مش 3 بعدی مورد بحث قرار گرفته است .
برای اضافه کردن این چرخش به شرایط تناوبی ، می توانید یک تبدیل را به یک نقشه میانی تنظیم کنید . انتخاب یک سیستم مختصات چرخشی برای این نقشه با زاویه اویلر α برابر با T cp ، تبدیل مناسب را اعمال خواهد کرد.
دوره کوتاه پیچ خورده
استفاده از تناوب پیچ خورده بر اساس مشاهده است که الگوی به محض بازگشت یک سیم زره خاص به موقعیت اولیه خود با توجه به یک فاز خاص، بدون توجه به جهت سطح مقطع کلی، خود را تکرار می کند. با این حال، اگر به نتایج دقیقتر نگاه کنید، خواهید دید که به محض اینکه هر سیم زرهی به آن موقعیت خاص رسید، الگوی خود را تکرار میکند – البته با فرض اینکه همه سیمهای زره یکسان باشند .
با این دانش میتوانید تناوب را برای “اتصال” هر سیم زره با همسایهاش، به جای خودش، پیکربندی کنید [ 3 ]. فاصله ای که طول می کشد تا سیم زره بعدی به موقعیتی برسد که سیم اولی داشت، کابین CP تقسیم بر تعداد سیم های زره است : بازوی N. مخصوصاً برای کابلهایی که تعداد سیمهای زرهی زیادی دارند، این به معنای کاهش گسترده اندازه مدل، هم از نظر عددی و هم از نظر هندسی است. شکل 4 را ببینید .
حلقه حاصل از قطعات کوتاه سیم زره میتواند بهعنوان برشی از کابل واقعی دیده شود، یا تعدادی بخش کوچک از سیم زره که بهصورت سری به هم متصل شدهاند تا یک سیم زره تمام دورهای را تشکیل دهند: این دو توصیف معادل هستند .

شکل 4: مش در زره در جهت عقربه های ساعت می چرخد، در حالی که مش باقی مانده در خلاف جهت عقربه های ساعت می چرخد. صفحه تناوب منبع در پایین و مقصد در بالا قرار دارد.
تناوب پیچ خورده کوتاه و انطباق مش
تناوب کوتاه پیچ خورده کاملاً رایگان نیست، با این حال: روش مش بندی نیاز به توجه بیشتری دارد. اگر قرار است مش ها در دو صفحه تناوب برابر باشند – برای به دست آوردن مش های منطبق ، به آموزش هندسه و مش 3 بعدی مراجعه کنید – شبکه سطح مقطع هر یک از سیم های زره باید یکسان باشد. به هر حال، تناوب کوتاه پیچ خورده باعث می شود که سیم های زره هنگام رفتن از هواپیمای مبدا به هواپیمای مقصد، مکان خود را تغییر دهند.
شکل 4 را یک بار دیگر در نظر بگیرید : حلقه ای که شامل سیم های زره است دارای پیچش در جهت عقربه های ساعت است، در حالی که بقیه مش در خلاف جهت عقربه های ساعت می چرخد. پس از طی مسافتی  ، سطح مقطع یکسان به نظر می رسد – البته با زاویه تابیده شده
، سطح مقطع یکسان به نظر می رسد – البته با زاویه تابیده شده  ، و سیم های زرهی یک موقعیت را تغییر داده اند. برای دامنههایی که با رنگ زرد نشان داده شدهاند، از مش جارو شده استفاده میشود و مطابقت مش به طور طبیعی در آنجا دنبال میشود. برای سطوح خاکستری، باید مراقب باشید تا مطمئن شوید که مش در هواپیما مقصد به همان درجه – و در همان جهت – چرخش مش در فازها باشد.
، و سیم های زرهی یک موقعیت را تغییر داده اند. برای دامنههایی که با رنگ زرد نشان داده شدهاند، از مش جارو شده استفاده میشود و مطابقت مش به طور طبیعی در آنجا دنبال میشود. برای سطوح خاکستری، باید مراقب باشید تا مطمئن شوید که مش در هواپیما مقصد به همان درجه – و در همان جهت – چرخش مش در فازها باشد.
در عمل، این بدان معنی است که دایره ای که محیط بیرونی مدل را مشخص می کند، باید بخشی از فازها و صفحه های صفحه کار (wp1) باشد . بخشی از صفحه تناوب که بیرون کابل است و قسمتی که بین صفحه نمایش و زره قرار دارد، باید با استفاده از عملیات Copy Face از مبدا تا مقصد کپی شود. علاوه بر این، مش در داخل و اطراف سیم های زره باید اصلاح شود تا اطمینان حاصل شود که مش برای هر یک از آنها یکسان است.
دوره تناوبی کوتاه و زره های دوتایی
برای یک مارپیچ منفرد، تناوب “مستقیم” به مدلی به اندازه طول لایه نیاز دارد – اما تناوب پیچ خورده از هر طولی پشتیبانی می کند. برای یک مارپیچ دوتایی با طولهای پایه جداگانه، تناوب “مستقیم” به کمترین مضرب مشترک از دو طول خواب نیاز دارد (که ممکن است بیش از 40 متر باشد) – اما تناوب پیچ خورده فقط به طولی برابر با کابین CP (که حدود 1.6 متر است ) نیاز دارد. مورد ما). اکنون، با استفاده از تناوب کوتاه پیچ خورده، می توانید این را حتی بیشتر کاهش دهید، به 1.5 سانتی متر (با فرض 110 سیم زره یکسان).
بنابراین، چه اتفاقی می افتد اگر یک زره دوتایی به آن اضافه کنید؟




