چرا این همه استرس و فشار؟

در مکانیک سازه با تعاریف زیادی از تنش و کرنش مواجه خواهید شد. ممکن است استرس دوم پیولا-کیرشهوف یا فشار لگاریتمی باشد . در این پست وبلاگ ما این مقادیر را بررسی خواهیم کرد، در مورد اینکه چرا نیاز به تنوع بسیاری از تنش ها و کرنش ها وجود دارد، بحث خواهیم کرد و پیامدهای آن را برای شما به عنوان یک تحلیلگر اجزای محدود روشن خواهیم کرد. عبارات و تبدیل‌های تانسور تعیین‌کننده را می‌توان در بسیاری از کتاب‌های درسی و همچنین از طریق برخی پیوندهای وب در انتهای این پست وبلاگ یافت، بنابراین در اینجا به تفصیل آورده نمی‌شوند.

تست کشش

هنگام ارزیابی داده های مکانیکی یک ماده، انجام آزمایش کشش تک محوری معمول است. آنچه در واقع اندازه گیری می شود منحنی نیرو در مقابل جابجایی است، اما برای اینکه این نتایج مستقل از اندازه نمونه باشد، نتایج معمولاً به صورت تنش در مقابل کرنش ارائه می شوند . اگر تغییر شکل ها به اندازه کافی بزرگ باشند، یک سوال این است: آیا تنش را بر اساس سطح مقطع اولیه نمونه محاسبه می کنید یا بر اساس سطح فعلی؟ پاسخ این است که هر دو تعریف استفاده می شود و به ترتیب استرس اسمی و استرس واقعی نامیده می شوند .

سوال دوم و نه چندان واضح این است که چگونه کشش نسبی ، یعنی کرنش را اندازه گیری کنیم. کرنش مهندسی به عنوان نسبت بین ازدیاد طول و طول اولیه تعریف می شود.. با این حال، برای کشش های بزرگتر، استفاده از هر دو کشش رایج تر است یا کرنش واقعی (کرنش لگاریتمی) .

کرنش واقعی در آزمایش فلز رایج‌تر است، زیرا برای بسیاری از مدل‌های پلاستیسیته مناسب است. برای مواد با کشیدگی احتمالی بسیار زیاد، مانند لاستیک، کشش پارامتر رایج تری است. توجه داشته باشید که برای مواد تغییر شکل نیافته، کشش است.

برای استفاده از داده های اندازه گیری شده در تجزیه و تحلیل، باید از دو مورد زیر اطمینان حاصل کنید:

نحوه تعریف تنش و کرنش در آزمون
نرم افزار تجزیه و تحلیل شما به چه شکلی از آن برای یک مدل ماده خاص انتظار دارد

تبدیل داده های تک محوری دشوار نیست، اما نباید فراموش شود.

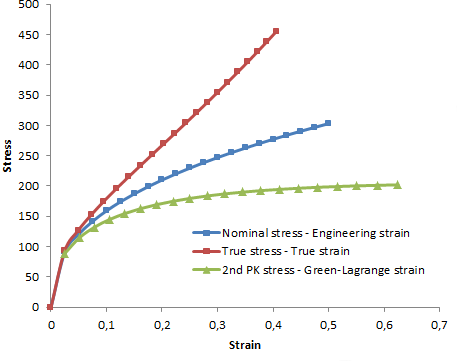
منحنی‌های تنش-کرنش برای همان آزمایش کششی.

غیرخطی بودن هندسی

اکثر مسائل مکانیک سازه را می توان با این فرض تحلیل کرد که تغییر شکل ها در مقایسه با ابعاد سازه آنقدر کوچک هستند که می توان معادلات تعادل را برای هندسه تغییر شکل نیافته فرموله کرد. در این حالت، تمایز بین معیارهای مختلف تنش و کرنش از بین می رود. اگر جابجایی ها، چرخش ها یا کرنش ها به اندازه کافی بزرگ شوند، غیرخطی بودن هندسی باید در نظر گرفته شود. این زمانی است که ما شروع به در نظر گرفتن این موضوع می کنیم که عناصر ناحیه واقعاً تغییر می کنند، بین طول اصلی و طول تغییر شکل یافته تمایز وجود دارد و ممکن است جهت ها در طول تغییر شکل تغییر کند. چندین روش معادل ریاضی برای نمایش چنین تغییرشکل های محدودی وجود دارد.

برای آزمون تک محوری بالا، نمایش های مختلف نسبتاً مستقیم هستند. اما در زندگی واقعی، هندسه ها سه بعدی هستند، حالت های تنش چند محوری دارند و ممکن است در فضا بچرخند. حتی اگر فقط همان تست کششی را در نظر بگیریم، تنش و کرنش را در یک سطح مشخص ثابت نگه داریم و سپس نمونه را بچرخانیم، سؤالاتی پیش می‌آید. چه نتایجی می توانیم انتظار داشته باشیم؟ آیا انتظار می رود مقادیر مولفه های تنش و کرنش تغییر کند یا خیر؟

اندازه گیری استرس

اساسی ترین و متداول ترین کمیت تنش تنش کوشی است که به عنوان تنش واقعی نیز شناخته می شود . با مطالعه نیروهای وارد بر یک عنصر مساحت بینهایت کوچک در جسم تغییر شکل یافته تعریف می شود . هر دو مولفه نیرو و نرمال به ناحیه دارای جهت ثابت در فضا هستند. این بدان معنی است که اگر یک جسم تحت فشار تحت یک چرخش خالص قرار گیرد، مقادیر واقعی اجزای تنش تغییر می کند. آنچه در ابتدا حالت تنش تک محوری بود ممکن است به یک تانسور کامل با هر دو مؤلفه تنش نرمال و برشی تبدیل شود. در بسیاری از موارد، این نه چیزی است که می خواهید استفاده کنید و نه آن چیزی است که انتظار دارید.

به عنوان مثال یک ماده ارتوتروپیک با الیافی که جهت خاصی دارند در نظر بگیرید. بسیار محتمل تر است که بخواهید تنش را در جهت فیبر ببینید، حتی اگر جزء چرخانده شده باشد. استرس دوم پیولا-کیرشهوفاین خاصیت را دارد در امتداد جهت مواد تعریف شده است. در شکل زیر، یک تیر کنسول مستقیم در نوک با یک گشتاور خالص در معرض خمش قرار گرفته است. مولفه xx تنش کوشی (بالا) و تنش دوم Piola-Kirchhoff (در زیر) نشان داده شده است. از آنجایی که تنش به صورت فیزیکی در امتداد تیر هدایت می شود، جزء xx تنش کوشی (که مربوط به جهت x سراسری است) با انحراف کاهش می یابد. تنش دوم Piola-Kirchhoff با این حال، توزیع ضخامت یکسانی را در تمام طول تیر دارد، حتی در پیکربندی تغییر شکل یافته.

استرس کوشی و دوم پیولا-کیرشهوف
تنش کوشی و دوم Piola-Kirchhoff برای یک تیر اولیه مستقیم با ممان خمشی ثابت.

یکی دیگر از معیارهای استرس که ممکن است با آن مواجه شوید، استرس اول پیولا-کیرشهوف است . این یک تعمیم چند محوری تنش اسمی (یا مهندسی) است. تنش به عنوان نیرویی در پیکربندی فعلی که بر ناحیه اصلی وارد می شود تعریف می شود. اولین Piola-Kirchhoff یک تانسور نامتقارن است و به همین دلیل کار کردن با آن جذابیت کمتری دارد.

گاهی اوقات ممکن است با استرس Kirchhoff نیز مواجه شوید . تنش Kirchhoff فقط تنش کوشی است که با تغییر حجم کاهش می یابد. اهمیت فیزیکی کمی دارد، اما می تواند در برخی از عملیات های ریاضی و عددی راحت باشد.

متأسفانه، حتی بدون چرخش، مقادیر واقعی تمام این نمایش‌های تنش یکسان نیستند. همه آنها با توجه به تغییرات حجمی و کشش های موضعی مقیاس متفاوتی دارند. این در نمودار زیر نشان داده شده است. مولفه xx از چندین معیار تنش در انتهای ثابت تیر، جایی که محور تیر با محور x منطبق است، رسم می‌شود. در مرکز تیر، جایی که کرنش‌ها و در نتیجه تغییرات حجم کم است، همه مقادیر به یکدیگر نزدیک می‌شوند. بنابراین برای موردی با چرخش بزرگ اما کرنش های کوچک، نمایش تنش را می توان به عنوان چرخش خالص همان تانسور تنش مشاهده کرد.

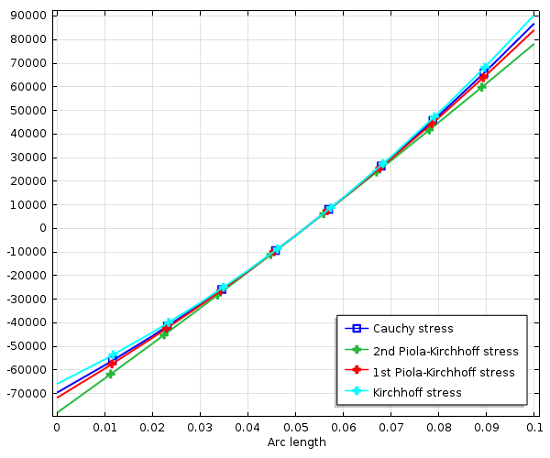
نمودار توزیع تنش محوری در انتهای ثابت تیر
توزیع تنش محوری در انتهای ثابت تیر.

اگر می‌خواهید نیروی حاصل یا لحظه‌ای را روی یک مرز مشخص محاسبه کنید، واقعاً فقط دو گزینه ممکن وجود دارد: یا تنش کوشی را روی مرز تغییر شکل‌داده‌شده ادغام کنید، یا تنش اول پیولا-کیرشهوف را روی همان مرز در پیکربندی تغییرشکل‌نشده ادغام کنید. . در COMSOL Multiphysics این مربوط به انتخاب “Spatial frame” یا “Material frame” در تنظیمات برای اپراتور ادغام است.

اقدامات کرنش

هنگام بررسی تست کشش تک محوری بالا، سه نمایش مختلف از کرنش معرفی شد. تعمیم همه آنها به موارد چند محوری امکان پذیر است، اما برای سویه واقعی این امر بی اهمیت نیست. این کار باید از طریق نمایشی در جهت‌های کرنش اصلی انجام شود زیرا این تنها راه برای گرفتن لگاریتم یک تانسور است. نمایش تانسور کلی کرنش لگاریتمی اغلب کرنش هنکی نامیده می شود .

همچنین بسیاری از نمایش های احتمالی دیگر از تغییر شکل وجود دارد. با این حال، هر نمایش معقولی باید بتواند چرخش صلب یک جسم بدون کرنش را بدون ایجاد هیچ فشاری نشان دهد. کرنش مهندسی در اینجا شکست می‌خورد، بنابراین نمی‌توان از آن برای موارد غیرخطی هندسی عمومی استفاده کرد. یکی از گزینه های رایج برای نشان دادن سویه های بزرگ، سویه گرین-لاگرانژ است. این شامل مشتقاتی از جابجایی ها با توجه به پیکربندی اصلی است. بنابراین مقادیر نشان‌دهنده کرنش‌ها در جهت‌های مادی، مشابه رفتار تنش دوم Piola-Kirchhoff است. این اجازه یک تفسیر فیزیکی را می دهد، اما باید متوجه شد که حتی برای یک حالت تک محوری، کرنش گرین-لاگرانژ با توجه به جابجایی به شدت غیرخطی است. اگر جسمی به دو برابر طول اصلی خود کشیده شود، کرنش گرین-لاگرانژ 1.5 در جهت کشش است. اگر جسم تا نصف طول خود فشرده شود، کرنش به 0.375- می رسد.

یک کمیت حتی اساسی‌تر، گرادیان تغییر شکل است ،، که مشتقات مختصات تغییر شکل یافته را با توجه به مختصات اصلی دارد،. گرادیان تغییر شکل شامل تمام اطلاعات در مورد تغییر شکل موضعی در جامد است و می تواند برای تشکیل بسیاری از کمیت های کرنش دیگر استفاده شود. به عنوان مثال، سویه گرین-لاگرانژ است. یک تانسور کرنش مشابه، اما بر اساس مشتقات با توجه به مختصات در پیکربندی تغییر شکل یافته، تانسور کرنش Almansi است .. سپس تانسور کرنش Almansi به جهت های ثابت در فضا اشاره می کند.

مقادیر مزدوج

یک راه کلی برای بیان مسئله مکانیک پیوسته استفاده از یک فرمول ضعیف است. در مکانیک این به عنوان اصل کار مجازی شناخته می شود، که بیان می کند که کار داخلی انجام شده توسط یک تغییر کرنش بینهایت کوچک که بر روی تنش های فعلی انجام می شود برابر است با کار خارجی انجام شده توسط یک جابجایی مجازی متناظر بر روی بارها. سپس معیارهای تنش و کرنش باید به گونه‌ای انتخاب شوند که محصول آنها چگالی انرژی دقیقی ارائه دهد. این چگالی انرژی ممکن است به حجم تغییر شکل نیافته یا تغییر شکل یافته مربوط باشد، بسته به این که آیا کار مجازی داخلی بر روی هندسه اصلی یا تغییر شکل یافته یکپارچه شده است.

در جدول زیر، برخی از جفت‌های تنش-کرنش مزدوج مربوطه خلاصه شده‌اند:

نژاد	فشار	تقارن	جلد	گرایش
کرنش مهندسی (بر اساس هندسه تغییر شکل یافته)؛ فشار واقعی؛ سویه المانسی	کوشی (استرس واقعی)	متقارن	ناقص شده	فضایی
کرنش مهندسی (بر اساس هندسه تغییر شکل یافته)؛ فشار واقعی؛ سویه المانسی	کیرشهوف	متقارن	اصلی	فضایی
گرادیان تغییر شکل	اولین پیولا-کیرشهوف (استرس اسمی)	غیر متقارن	اصلی	مختلط
سویه سبز-لاگرانژ	دوم Piola-Kirchhoff (استرس مادی)	متقارن	اصلی	مواد

در رابط مکانیک جامد در COMSOL Multiphysics، اصل کار مجازی همیشه در هندسه تغییر شکل نیافته (“قاب ماده”) بیان می شود. سپس از کرنش های گرین-لاگرانژ و تنش های دوم پیولا-کیرشهوف استفاده می شود. چنین فرمولی گاهی اوقات فرمول “کل لاگرانژی” نامیده می شود. فرمولاسیونی که در عوض بر اساس مقادیر موجود در پیکربندی فعلی است، فرمول “لاگرانژی به روز شده” نامیده می شود.