رابط حمل و نقل الکتروفورتیک، حمل و نقل گونه های باردار و بدون بار را مدل می کند، و علاوه بر این، معادله تعادل بار را برای پتانسیل الکترولیت تنظیم می کند.
غلظت گونه ها، c i (واحد SI: mol/m 3 )، و پتانسیل، 
(واحد SI: V) نشان داده می شود.
(واحد SI: V) نشان داده می شود.گونه ها با انتشار، مهاجرت، و (به صورت اختیاری) همرفت با توجه به مجموعه معادلات نرنست-پلانک منتقل می شوند. شار کل گونه i با N i (واحد SI: mol/(m2 · s)) با توجه به
(6-62)
که در آن D i (واحد SI: m2 / s) ضریب انتشار، z i (1) بار مربوطه، u m,i (واحد SI: s·mol/kg) تحرک و u (واحد SI: m/ است. ث) بردار سرعت. J i نشان دهنده شار مولی نسبت به انتقال همرفتی است (واحد SI: mol/(m2 · s)). برای توصیف دقیق تئوری این معادلات و شرایط مرزی مختلف، به نظریه انتقال رابط گونه های رقیق مراجعه کنید .
معادله تعادل شارژ
بردار جریان، i l (A/m 2 )، به صورت تعریف می شود
(6-63)
که در آن جمع بر روی تمام گونه های الکترولیت انجام می شود.
معادله حاکم برای پتانسیل الکترولیت است
(6-64)
که در آن Ql (واحد SI: A/m 3 ) منبع جریان الکترولیت است که برای مثال از واکنش های الکترود متخلخل ناشی می شود . برای حوزه های الکترود غیر متخلخل، این عبارت منبع معمولاً صفر است.
غلظت پروتون و هیدروکسید و قدرت الکتریکی
با فرض اینکه تعداد کل گونه ها N + 2 باشد ، فرض الکتروخنثی بودن است.
(6-65)
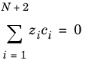
در سیستم های مبتنی بر آب، گونه های H+ و OH- همیشه وجود دارند. واکنش یونیزاسیون خودکار برای آب است
(6-66)
این واکنش با پیروی از رابطه تعادل سریع است
(6-67)
کجا 
.
.اکنون، شرایط الکتروخنثی، شامل دو گونه اضافی H+ و OH- می‌خواند
(6-68)
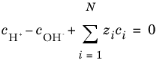
از ترکیب این دو معادله عبارات جبری زیر برای غلظت H+ و OH- حاصل می شود.
(6-69)
و
(6-70)
جایی که
(6-71)
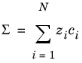
معادلات موازنه جرم برای گونه های تفکیک
مجموعه ای از گونه های Si را که مراحل تفکیک k را توصیف می کند، فرض کنید
(6-72)
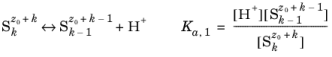
به
(6-73)
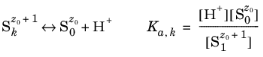
که z 0 بار (ظرفیت) گونه S 0 (که هیچ پروتون قابل تجزیه ای ندارد) و Ka ,j ثابت اسیدی (تعادل) واکنش تفکیک j است . براکت های “[ ]” در اینجا فعالیت گونه را نشان می دهند. شارژ هر گونه با توجه به z 0 +i همیشه از شاخص i کسر می شود و از این به بعد حذف می شود.
اگر فعالیت پروتون مشخص باشد، هر گونه S m ممکن است با استفاده از هر گونه دیگر Sl مطابق با آن بیان شود
(6-74)
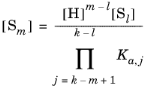
اگر m > l و
(6-75)
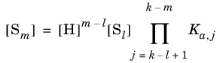
اگر l > m .
با تنظیم m = i و نشان دادن شار گونه i با Ni با استفاده از معادله 6-62 ، معادله تعادل جرم برای غلظت c i هر زیرگونه i در زنجیره تفکیک است.
(6-76)
که در آن Req ,i,j منبع واکنش ناشی از مرحله تفکیک j است (با R eq ,i,k+ 1 = 0) و Ri هر منبع واکنش اضافی است .
سهم منبع واکنش از مراحل تفکیک معمولاً مشخص نیست، اما ممکن است با جمع کردن تمام معادلات موازنه جرم لغو شود، که منجر به
(6-77)
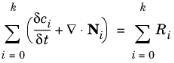
فرمولاسیون یونیزاسیون متوسط برای مولکول های بزرگ
مولکول های بزرگ پروتئین معمولاً در معرض تعداد زیادی از مراحل تفکیک هستند.
به عنوان یک راه جایگزین برای زنجیره طولانی مراحل تفکیک برای توصیف انتقال پروتئین، می‌توان انتقال پروتئین را بر اساس میانگین تعداد پروتون‌های ( 
1) حذف شده از مولکول فرموله کرد. معمولاً به عنوان تابعی از pH بر اساس داده های تجربی ارائه می شود. پس میانگین بار گونه برابر است 
، به طوری که شار گونه به صورت زیر نوشته می شود:
1) حذف شده از مولکول فرموله کرد. 
معمولاً به عنوان تابعی از pH بر اساس داده های تجربی ارائه می شود. پس میانگین بار گونه برابر است 
، به طوری که شار گونه به صورت زیر نوشته می شود:(6-78)
و به طور مشابه اضافه شدن به شرط خنثی بودن بار است 
.
.هنگام در نظر گرفتن سهم در معادله فعلی و تعادل شارژ، باید در نظر گرفت که میانگین مجذور شارژ، , 
برابر با “متوسط بار مجذور” نیست 
( مراجعه 1 ).
برابر با “متوسط بار مجذور” نیست 
( مراجعه 1 ).اضافه بر بردار چگالی جریان است
(6-79)
میانگین تعداد پروتون های حذف شده از پروتون معمولاً به pH بستگی دارد. اگر میانگین تعداد پروتون های حذف شده فقط به pH بستگی داشته باشد، میانگین مجذور تعداد پروتون های حذف شده را می توان به صورت زیر نوشت:
(6-80)
و از این می توان میانگین بار مجذور را بر اساس آن استخراج کرد
(6-81)
روابط انتشار- تحرک
شعاع استوکس r یک مولکول به میزان انتشار مربوط است
(6-82)
جایی که μ (واحد SI: Pa·s) ویسکوزیته دینامیکی و k ثابت بولتزمن است.
برای مولکول های کوچک، اغلب از رابطه نرنست-اینشتین بین انتشار و تحرک استفاده می شود.
(6-83)
برای مولکول‌های بزرگتر، مانند پروتئین‌ها، تحرک ممکن است بر اساس بیان Debye-Hückel-Henry ( مراجعه 2 ) محاسبه شود.
(6-84)
که در آن κ (1/m) پارامتر Debye است که به قدرت یونی محلول بستگی دارد، برای محلول های ایده آل به صورت تعریف می شود.
(6-85)
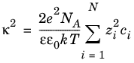
که در آن ε ثابت دی الکتریک سیال و ε 0 گذردهی فضای آزاد است. ( 
در صورت موجود بودن در فرمول بالا هنگام محاسبه قدرت یونی باید استفاده شود).
در صورت موجود بودن در فرمول بالا هنگام محاسبه قدرت یونی باید استفاده شود).تابع f بالا بر اساس یک تابع سیگموئیدی است به طوری که از 1 برای 
تا 1.5 برای متغیر است 
. توجه داشته باشید که عبارت Debye-Hückel-Henry به تحرک نرنست-انیشتین به صورت 
.
تا 1.5 برای متغیر است 
. توجه داشته باشید که عبارت Debye-Hückel-Henry به تحرک نرنست-انیشتین به صورت 
.برای مولکول های بزرگتر (یون های ماکرو)، که در آن فاصله بین بارها در مقایسه با 1/ κ بزرگ است ، تقریب Linderstrøm-Lang سهم کمتری را در قدرت یونی فرض می کند به طوری که یون z -valent مانند یک یون تک ظرفیتی با یک یون رفتار می کند. z- برابر غلظت. برای مجموعه ای از مولکول های کوچکتر N – M و یون های ماکرو M ، پارامتر Debye به صورت تعریف می شود.
(6-86)
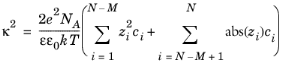
منابع
1. RA Mosher, DA Saville, and W. Thormann, The Dynamics of Electrophoresis , VCH Verlagsgesellschaft mbH, Weinheim, Germany, 1992.
2. RA Mosher, P. Gebauer, J. Caslavska, and W. Thormann, “Computer Simulation and Experimental Validation of the Electrophoretic Behavior of Proteins. 2. بهبود مدل و کاربرد در ایزوتااکوفورزیس، آنال. شیمی. ، جلد 64، صفحات 2991-2997، 1992.
