برای گسترش اعتبار معادله موج اغتشاش کوچک به امواج با دامنه محدود، باید اثرات غیرخطی را در نظر گرفت. ایده اول این است که رابطه فشار چگالی را به مرتبه دوم گسترش دهیم تا تأثیر امواج دامنه محدود را در بر گیرد. این می دهد
(2-20)
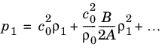
جایی که ما زیرنویس “1” را برای برجسته کردن کمیت های اغتشاش آکوستیک و زیرنویس “0” برای کمیت های ساکن نگه داشته ایم. رجوع کنید به رفر. 6 و 42 برای جزئیات. کمیت B / A پارامتر غیرخطی بودن است (رجوع کنید به شماره 51 ). این عبارت اساساً به این معنی است که بخشهای مختلف موج فشار صوتی با سرعتهای متفاوتی حرکت میکنند.
درج موارد فوق در معادله حاکم 2-11 (با حفظ اصطلاحات اتلاف دهنده) به معادله موج مرتبه دوم غیرخطی کامل منجر می شود. این معادل غیرخطی معادله 2-12 (یا در واقع معادل غیرخطی معادلات کامل آکوستیک ترموویسکوز) است. بعد فرض کنید که اثرات لایه مرزی را می توان نادیده گرفت و اثرات غیرخطی تجمعی بر اثرات غیرخطی محلی غالب می شود، برای مثال، زمانی که فاصله انتشار بیشتر از طول موج باشد. این منجر به معادله معروف وسترولت می شود (رجوع کنید به شماره 42 ) .
(2-21)
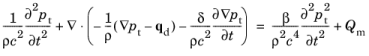
در اینجا ما نوسانات چگالی را حذف کرده و سپس زیرنویس ها را حذف کرده ایم. بنابراین، p t فشار آکوستیک (کل)، ρ چگالی ساکن، δ انتشار صدا، و β ضریب غیرخطی (مربوط به پارامتر غیرخطی B / A ) است.
معادله وسترولت از انتشار شوک ها پشتیبانی می کند. گرفتن شوک ها از نظر عددی سخت است و نیاز به افزودن تثبیت کننده دارند. برای مثال، می توان این کار را با افزودن قابلیت انتشار در نزدیکی محل ضربه انجام داد. یکی از روشها (که در COMSOL استفاده میشود) اضافه کردن یک عبارت انتشار موثر است که خوانده میشود
بالاترین میرایی مصنوعی در جایی حاصل می شود که فشار صوتی با بیشترین سرعت افزایش یا کاهش می یابد. در جایی که فشار ناپیوستهها را تحمل میکند، یعنی جایی که شوکها ایجاد میشوند، به حداکثر مقادیر خود میرسد. بنابراین این تکنیک تثبیت کننده شوک را فراهم می کند. رجوع کنید به رفر. 52 برای جزئیات بیشتر برای بدست آوردن مقدار مطلوب میرایی مصنوعی، شار q-لاپلاسین q و به اصطلاح ضریب q-لاپلاسی κ را مشخص کنید. توجه داشته باشید که میرایی نباید خیلی زیاد یا خیلی کم باشد. مقادیر خاص q و κبه مواد و فرکانس سیگنال ورودی بستگی دارد. دو پارامتری که تثبیت را کنترل می کنند نیاز به تنظیم دستی دارند. یک رویکرد پیشنهادی استفاده از یک مدل 1 بعدی ساده برای تنظیم پارامترها بر اساس خواص مواد سیال و محتوای فرکانس است.
آکوستیک غیرخطی — مدلسازی معادله 1 بعدی وسترولت : مسیر کتابخانه برنامه Acoustics_Module/Nonlinear_Acoustics/nonlinear_acoustics_westervelt_1d |




