مسائل آکوستیک استاندارد شامل حل تغییرات فشار آکوستیک کوچک (اغلب با p’ یا p 1 ) در بالای فشار پس زمینه ساکن/سکوت (اغلب p 0 یا p A نشان داده می شود ) است. از نظر ریاضی این نشان دهنده یک خطی سازی (بسط پارامتر کوچک) در اطراف مقادیر ساکن ساکن است.
معادلات حاکم برای مشکل جریان سیال بدون تلفات تراکم پذیر (بدون رسانش حرارتی و بدون ویسکوزیته)، معادله تکانه (معادله اویلر) و معادله پیوستگی است. اینها توسط:
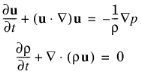
که ρ چگالی کل، p فشار کل، و u میدان سرعت کل است. در آکوستیک فشار کلاسیک، تمام فرآیندهای ترمودینامیکی برگشت پذیر و آدیاباتیک فرض می شوند که به عنوان یک فرآیند ایزنتروپیک شناخته می شود. انبساط پارامتر کوچک روی یک سیال ثابت با چگالی ρ 0 (واحد SI: kg/m3 ) و در فشار p 0 (واحد SI: Pa) انجام میشود به طوری که:
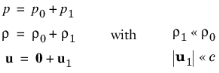
که در آن زیرنویس 1 تغییرات آکوستیک کوچک را نشان می دهد (گاهی اوقات به جای آن با علامت اول نشان داده می شوند). درج اینها در معادلات حاکم و تنها حفظ عبارات خطی در متغیرهای اغتشاش کوچک نتیجه می دهد.
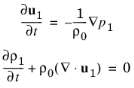
یکی از متغیرهای وابسته، چگالی، با بیان آن بر حسب فشار با استفاده از دیفرانسیل چگالی (خطیسازی) حذف میشود.
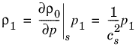
که در آن cs به عنوان سرعت (ایسنتروپیک) صوت (واحد SI: m/s) در آنتروپی ثابت s تشخیص داده می شود . لازم به ذکر است که این معادله برای چگالی پس زمینه با مقدار ثابت (نه وابسته به فضا) ρ 0 و فشار زمینه p 0 معتبر است . زیرنویس s در زیر حذف شده است. از عبارت بالا نیز چنین استنباط می شود که یکی دیگر از الزامات معتبر بودن آکوستیک خطی (تقریبا اغتشاش) این است که
در نهایت، با مرتب کردن مجدد معادلات (واگرایی معادله تکانه وارد شده در معادله پیوستگی) و حذف زیرنویس 1، معادله موج برای امواج صوتی در یک محیط بدون تلفات به دست میآید.
(1-1)
سرعت صوت به تراکم پذیری سیالی که در آن امواج در حال انتشار هستند مربوط می شود. ترکیب ρc 2 مدول حجیم نامیده می شود که معمولاً K نشان داده می شود ( واحد SI: N/m2 ) .
یک مورد خاص یک موج هارمونیک زمانی است که فشار آن با زمان تغییر می کند
که در آن ω = 2 π f (واحد SI: rad/s) فرکانس زاویه ای و f (واحد SI: هرتز) نشان دهنده فرکانس است. معادله موج برای امواج صوتی به معادله هلمهولتز کاهش می یابد:
(1-2)
که در آن نسبت ω / c به عنوان عدد موج k تشخیص داده می شود . این معادله همچنین می تواند به عنوان یک PDE مقدار ویژه برای حل حالت های ویژه و فرکانس های ویژه در نظر گرفته شود.
شرایط مرزی معمول برای معادله موج و معادله هلمهولتز عبارتند از:
• | مرزهای سخت صدا (دیوارها) |
• | مرزهای صدا-نرم |
• | شرایط مرزی امپدانس |
• | شرایط مرزی تشعشع |
یک مشتق دقیق از معادلات حاکم در زمینه تئوری برای شاخه آکوستیک فشار آورده شده است . برای انتشار امواج فشاری (آکوستیک) در یک سیال چسبناک و رسانای حرارتی، تئوری در زمینه تئوری برای شاخه آکوستیک ترموویسکوز و برای آکوستیک در رسانه های متحرک (هواآکوستیک) در زمینه تئوری برای شاخه هواآکوستیک ارائه شده است .




