واکنش های الکتروشیمیایی با استفاده از گره های واکنش الکترود یا واکنش الکترود متخلخل تعریف می شوند . واکنش الکترود با ترمودینامیک، سینتیک و استوکیومتری آن تعریف می شود. دومی شارهای جرمی، منابع و غرق‌های ناشی از چگالی جریان معین واکنش را توصیف می‌کند.
ترمودینامیک واکنش های الکتروشیمیایی
یک واکنش الکترولیتی شامل تبادل الکترون با الکترود است. چنین واکنشی به عنوان کاهش نوشته می شود، حتی اگر واکنش عمدتاً در جهت اکسیداتیو رخ دهد. مثلا:
این واکنش واکنش “نیمه سلولی” نامیده می شود، زیرا در یک رابط الکترود-الکترولیت خاص رخ می دهد. این نمی تواند به صورت مجزا اتفاق بیفتد، اما فقط زمانی که با یک واکنش نیمه سلولی دیگر در یک سلول الکتروشیمیایی دو الکترودی همراه شود. هر واکنش دارای یک تغییر انرژی گیبس است که تعیین می کند که آیا از نظر ترمودینامیکی مطلوب است یا خیر. تغییر انرژی گیبس منفی به این معنی است که واکنش به طور خود به خود ادامه می یابد – از نظر ترمودینامیکی “سرازیری” است.
تغییر انرژی گیبس با توجه به تفاوت پتانسیل تعادل از الکترود به الکترولیت مرتبط است:
که در آن Eq , m اختلاف پتانسیل در مقیاس مرجع خارجی است که واکنش در آن در تعادل است ( Δ G = 0 ). این پتانسیل تعادل یا پتانسیل کاهش (یا در خوردگی، پتانسیل خوردگی ) واکنش الکتروشیمیایی نامیده می شود و مقدار مطلق آن به انتخاب الکترود مرجع بستگی دارد.
 | پتانسیل های تعادل همیشه باید در مقابل یک مرجع خاص نقل شود. اگر مقیاس مرجع متفاوتی در بخش‌های مختلف مدل شما استفاده شود، ترمودینامیک سیستم ممکن است آنطور که انتظار می‌رود رفتار نکند. |
از رابطه ترمودینامیکی استاندارد
آن به شرح زیر است
این معادله نرنست است که یک عبارت ترمودینامیکی جهانی است. همیشه در مورد سیستم هایی که در تعادل ترمودینامیکی هستند صادق است. لزوماً برای سیستم هایی که در تعادل نیستند اعمال نمی شود.
با فرض اینکه گونه ها ایده آل هستند و اثرات فعالیت را می توان ثابت تلقی کرد، برای تبدیل بین گونه های احیا شده و اکسید شده تک مولکولی:
از این رو در حالت تعادل ، غلظت واکنش‌دهنده‌ها و محصولات در سطح الکترولیت-الکترود با بیانی مرتبط است که به اختلاف پتانسیل بین دو فاز و دو پارامتر واکنش بستگی دارد: n ، تعداد الکترون‌های منتقل شده به ازای هر مولکول کاهش می‌یابد. و E f ، پتانسیل کاهش رسمی واکنش در همان مقیاس پتانسیل اندازه گیری شده با اختلاف پتانسیل الکترود-الکترولیت است.
کمیت
به عنوان مازاد پتانسیل شناخته می شود و مخصوص واکنش خاصی است که در سطح مشترک رخ می دهد.
 |  هم به پتانسیل الکتریکی در الکترود  و هم به پتانسیل الکترولیت بستگی دارد  . در جایی که مقاومت قابل توجهی در برابر جریان از طریق محلول وجود دارد، اختلاف پتانسیل مربوطه به  نام افت اهمی ، موقعیت تعادل الکتروشیمیایی را تغییر می دهد. ممکن است پتانسیل اعمال شده اضافی در مدار الکتریکی برای به حرکت درآوردن یک مازاد پتانسیل معادل مورد نیاز باشد. |
سینتیک واکنش های الکتروشیمیایی
معادله نرنست موقعیت تعادل یک واکنش را به ما می گوید. با این حال، چیزی در مورد اینکه سیستم با چه سرعتی ممکن است به آنجا برسد، به ما نمی گوید. اگر یک محدودیت جنبشی وجود داشته باشد – یعنی اگر واکنش به کندی پیش رود – شرایط تعادل ممکن است هرگز مشاهده نشود. به عنوان یک مثال آشنا، الماس از نظر ترمودینامیکی ناپایدار است نسبت به واکنش برای تشکیل گرافیت در دما و فشار اتاق. با این حال، این واکنش از نظر جنبشی توسط انرژی فعال سازی گسترده برای جهت دهی مجدد اتم ها محدود می شود، به طوری که در عمل هرگز مشاهده نمی شود، و الماس از نظر فنی به عنوان فراپایدار توصیف می شود .
ما در بسیاری از زمینه های الکتروشیمیایی با همین موضوع روبرو هستیم. واکنش‌ها با محدودیت‌های جنبشی از رسیدن به تعادل خود جلوگیری می‌کنند. در واقع، غلبه بر کندی جنبشی طبیعی واکنش‌های سطحی مولکول‌های کوچک و غیرقطبی مانند هیدروژن و اکسیژن، کلید بسیاری از تحقیقات پیل سوختی است.
دو عبارت مهم وجود دارد که چگالی جریان ناشی از یک واکنش الکتروشیمیایی را به عنوان تابعی از مازاد پتانسیل و غلظت واکنش دهنده و محصول توصیف می کند. لازم به ذکر است که اعتبار این عبارات کلی نیست و هرگز نمی تواند جایگزین داده های سینتیکی تجربی در صورت موجود باشد.
اولین قانون تافل است که یک فرآیند آندی یا کاتدی برگشت ناپذیر را توصیف می کند:
ثابت A شیب تافل است و دارای واحدهای 1/V است. معمولاً نزدیک به مضرب نیم صحیح F/RT است و کمتر یا مساوی با nF/RT است . توجه داشته باشید که چگالی جریان مبادله مرجع i 0 باید برای واکنش مشخص شود. این طبق تعریف چگالی جریان است که در پتانسیل صفر رسم شده است.
 | قانون تافل فرض می کند که یک واکنش برگشت ناپذیر است. اگر در عمل واکنش معکوس رخ دهد، سینتیک تافل صحیح نخواهد بود. |
عبارت دوم معادله باتلر-ولمر است که یک فرآیند برگشت پذیر را توصیف می کند، به طوری که ممکن است جریان آندی یا کاتدی بسته به علامت و بزرگی مازاد پتانسیل جاری شود:
معادله باتلر-ولمر کلی ترین توصیف سینتیک الکترود است. بسیار سازگار است زیرا:
• | i 0 یک کمیت تجربی است. |
• | زمانی که i = 0 باشد با معادله نرنست مطابقت دارد ، بنابراین برای یک واکنش بسیار سریع (  ) معادله باتلر-ولمر همان اختلاف پتانسیل معادله نرنست را می دهد. این در شرایط مقاومت بالا نیز به همان اندازه صادق است. |
• | زمانی که عبارت آندی یا کاتدی غالب باشد، با معادله تافل موافق است. برای واکنش‌های بسیار برگشت‌ناپذیر (خیلی کم i 0 )، جریان قابل‌توجهی فقط برای مازاد پتانسیل بزرگ کشیده می‌شود، بنابراین معمولاً چنین است. |
برای بحث در مورد بیان باتلر-ولمر و تغییرات غلظت گونه های شرکت کننده، به بخش سینتیک باتلر-ولمر وابسته به غلظت زیر مراجعه کنید.
برای یک واکنش برگشت پذیر در بیش پتانسیل بسیار پایین ( η از مرتبه RT / F ~ 25 میلی ولت)، نمایی در معادله باتلر-ولمر را می توان خطی کرد:
 | استفاده از یک واکنش باتلر-ولمر خطی شده می تواند هنگام بررسی مسائل همگرایی یک مدل سودمند باشد. |
 | معادله خطی شده باتلر-ولمر برای اضافه پتانسیل های اعمال شده بزرگتر از ( RT / F) صحیح نیست . این حدود 25 میلی ولت در دمای اتاق است. خارج از این محدوده مناسب نیست و بنابراین استفاده از آن محدود به فرآیندهای الکتروشیمیایی است که منحصراً در چگالی جریان پایین رخ می‌دهند، مانند آبکاری الکتریکی یا طیف‌سنجی امپدانس الکتروشیمیایی. |
 | عبارات سینتیک الکترود |
شارها و منابع / سینک های ناشی از واکنش های الکترود
واکنش های الکترود منجر به شار مولکولی از گونه های واکنش دهنده به سطح الکترود یا از آن می شود. اگر انتقال جرم را در مدل خود لحاظ کنید، معمول است که شار یک گونه واکنش دهنده را در یک مرز با چگالی جریان واکنش الکترود جفت کنید (طبق قانون الکترولیز فارادی).
جفت شار شیمیایی به چگالی جریان الکتریکی در برخی از رابط های الکتروشیمی با تعریف استوکیومتری واکنش در گره های واکنش الکترود و واکنش الکترود متخلخل به طور خودکار انجام می شود . در رابط های حمل و نقل گونه های شیمیایی، کوپلینگ باید به صورت دستی توسط گره های اتصال سطحی الکترود تنظیم شود . هنگام مدل سازی الکترودهای متخلخل، گره جفت کننده مربوطه برای ایجاد منبع/سینک در یک دامنه، گره جفت الکترود متخلخل است .
درمان ریاضی را می توان با عبارت زیر خلاصه کرد:
این بدان معنی است که شار Nj گونه های شیمیایی j به سطح متناسب با چگالی جریان i m ناشی از واکنش m است که در سطح مشترک الکترود-الکترولیت کشیده شده است . ثابت تناسب، عدد استوکیومتری گونه ها تقسیم بر تعداد الکترون های منتقل شده در واکنش m در جهت تقلیل و F ثابت فارادی (96485 C/mol، بار مطلق یک مول الکترون) است.
به این ترتیب، دانش استوکیومتری یک واکنش الکتروشیمیایی اجازه می دهد تا شار محلی یک گونه شیمیایی با چگالی جریان حاصل از آن واکنش جفت شود. توجه داشته باشید که چندین واکنش ممکن است به طور همزمان در یک الکترود انجام شود و سهم آنها در چگالی جریان به سادگی جمع می شود.
 | ضرایب استوکیومتری گونه های شیمیایی در یک واکنش الکتروشیمیایی به طور معمول با واکنش رو به جلو در جهت کاهش نوشته می شود، حتی اگر در عمل در سیستم واکنش عمدتاً در جهت دیگر انجام شود. |
 | COMSOL Multiphysics از قرارداد استاندارد استفاده می کند که جریان آندی (اکسیداتیو) مثبت است. جریان کاتدی (کاهشی) منفی است. |
تعریف سینتیک باتلر-ولمر وابسته به تمرکز
اگر غلظت در سطح الکترود تغییر کند، این روی سینتیک موضعی تأثیر خواهد گذاشت. بیان سینتیک باتلر-ولمر با در نظر گرفتن سرعت یک واکنش ردوکس به دست می آید
(2-1)
به عنوان مجموع نرخ های رو به جلو و عقب بر اساس:
(2-2)
که در آن k fwd و k rwd ثابت‌های سرعت واکنش هستند و c O و c R به ترتیب فعالیت‌های گونه‌های اکسید شده و کاهش‌یافته زوج ردوکس هستند. پتانسیل E در اینجا به صورت تعریف می شود
(2-3)
و ضرایب انتقال برابر با مجموع الکترون ها در واکنش انتقال بار است
(2-4)
با تعریف پتانسیل تعادلی که در آن سرعت واکنش رو به جلو و واکنش رو به عقب برابر است، می توان معادله 2-1 را معادل معادله متداول باتلر-ولمر نشان داد:
(2-5)
در این فرمول، با فرض اینکه ضرایب استوکیومتری گونه های اکسید شده و احیا شده به ترتیب 1- و 1 باشد، چگالی جریان مبادله، i 0 ، به صورت زیر تعریف می شود:
(2-6)
که در آن i 0، ref چگالی جریان مبادله در برخی شرایط مرجع انتخابی است و مازاد پتانسیل به صورت تعریف می شود
(2-7)
که در آن Eq پتانسیل تعادل است با معادله نرنست به صورت تعریف می شود
(2-8)
و Eq ، ref پتانسیل تعادل در همان شرایط مرجع است.
معمولاً شرایط استاندارد به عنوان غلظت های مرجع استفاده می شود، به عنوان مثال غلظت 1 M برای یون ها در محلول های آبی.
توجه داشته باشید که در معادله 2-5 هر دو i 0 و Eq وابسته به غلظت هستند. این در هنگام مدل‌سازی سلول‌های الکتروشیمیایی از جمله انتقال جرم، اشکالات عددی دارد، زیرا برای غلظت‌های پایین گونه‌های شرکت‌کننده (یعنی زمانی یا )، ممکن است فاکتور در طول فرآیند حل نامشخص شود. بیان شکل معادله 2-2 مطلوب تر است زیرا این عبارات حاوی یک وابستگی خطی ساده به فعالیت های گونه است.
یک راه حل متداول برای این مسئله بازنویسی عبارت Butler-Volmer با تعریف مازاد پتانسیل با توجه به یک حالت مرجع ثابت برای فعالیت های c R , ref و c O , ref (معمولاً مربوط به ورودی یا غلظت اولیه) است که منجر به
(2-9)
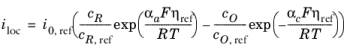
جایی که
(2-10)
توجه داشته باشید که معادله 2-9 اکنون دارای یک وابستگی خطی به فعالیت های c O و c R است .
