تعدادی از عبارات تحلیلی مختلف برای چگالی جریان عمود بر سطح الکترود، i loc ،m ، موجود است. در پاراگراف های بعدی، شاخص m حذف شده است. همه پارامترها به یک واکنش خاص اشاره می کنند.
پتانسیل تعادل و مازاد پتانسیل
سرعت واکنش های الکتروشیمیایی را می توان با ربط دادن سرعت واکنش به پتانسیل بیش از حد فعال سازی توصیف کرد. برای یک واکنش الکترود، مازاد پتانسیل فعالسازی که η (V) نشان داده میشود ، به صورت زیر است:
که در آن Eq پتانسیل تعادل را نشان می دهد .
معادله باتلر-ولمر
یک عبارت رایج برای چگالی جریان به عنوان تابعی از مازاد پتانسیل فعال سازی، در مدل سازی سیستم های الکتروشیمیایی، معادله باتلر-ولمر است:
که α c (بدون واحد) نشان دهنده ضریب انتقال بار کاتدی، α a (بدون واحد) ضریب انتقال بار آندی، و i 0 (واحد SI: A/m 2 ) چگالی جریان تبادلی است.
لازم به ذکر است که، اگرچه به طور گسترده برای انواع واکنش ها در جامعه الکتروشیمیایی استفاده می شود، معادله باتلر-ولمر در اصل برای واکنش های انتقال تک الکترون به دست آمده است (مثلاً به این معنی است که واکنش شامل شکستن یا ایجاد یک ماده شیمیایی نیست. رابطه، رشته).
وابستگی به تمرکز و چگالی جریان مبادله
چگالی جریان مبادله به طور کلی وابسته به غلظت است. برای شرایط خاص، می توان عبارات تحلیلی را برای i 0 استخراج کرد . با فرض یک پتانسیل تعادل وابسته به غلظت که توسط معادله نرنست تعریف شده است (به بخش قبلی پتانسیل های تعادل و معادله نرنست مراجعه کنید ) ، سینتیک برای پیروی از قانون عمل جرم، و شرطی که αa + α c = n ، سپس چگالی جریان تبادلی به صورت زیر می شود:
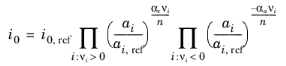
که در آن i 0 ، ref چگالی جریان مبادله (واحد SI: A/m 2 ) در حالت مرجع است. عبارت فوق را می توان از قانون عمل انبوه مشتق کرد که عبارت زیر را برای چگالی جریان محلی به دست می دهد:
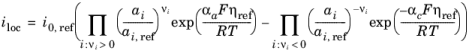
که در آن مازاد پتانسیل η ref (واحد SI: V) با استفاده از حالت مرجع اندازه گیری می شود که به دست می آید:
این شکل اخیر از معادله باتلر-ولمر، که در آن مازاد پتانسیل مرجع و چگالی جریان مبادله با غلظت تغییر نمی کند، معمولاً از نظر عددی ارجح است.
قانون عمل جرم معمولاً برای تعریف واکنش های پیچیده شامل مراحل الکترون های متعدد مناسب نیست. برای واکنشهای چند الکترونی خاص، که در آن یک مرحله انتقال الکترون محدودکننده سرعت است، میتوان یک عبارات باتلر-ولمر را با استفاده از رابطه زیر برای چگالی جریان مبادله استخراج کرد (رجوع کنید به شماره 1 ) :
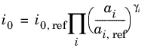
که γ i ضرایب نمایی عمومی هستند. برای این مورد، α a و α c ممکن است به طور مستقل تعریف شوند. با تنظیم مجدد عبارت Butler-Volmer با استفاده از η ref مشابه آنچه در مورد قانون عمل جرمی در بالا انجام شد، ضرایب γi به ترتیب واکنش آندی، ξa ، i ، یا کاتدی، ξc ، i مربوط می شود .
و
چگالی جریان مبادله و ثابت نرخ
در الکتروآنالیز، سینتیک الکترود را معمولاً بر حسب ثابتهای سرعت تعریف میکند تا چگالی جریان مبادله.
به عنوان مثال، برای یک زوج ردوکس یک الکترون با غلظت های c o و cr ، با غلظت مرجع یکسان c ref برای هر دو گونه، و i 0، ref = k 0 F c ref ، عبارت قانون عمل جرم در بالا را می توان به صورت بازنویسی کرد.
که در آن k 0 (m/s) ثابت سرعت ناهمگن است.
سینتیک نوع باتلر-ولمر وابسته به غلظت عمومی
این نوع بیان آزادی بیشتری را به کاربر میدهد تا انواع عبارات باتلر-ولمر وابسته به غلظت را تعریف کند، جایی که شرایط آندی و کاتدی بیان چگالی جریان، معمولاً بسته به غلظتهای محلی گونههای الکترواکتیو در سطح الکترود، ممکن است به صورت جداگانه باشد. تعریف شده است:
در اینجا CR و CO عباراتی بدون بعد هستند که وابستگی به گونه های کاهش یافته و اکسید شده را در واکنش توصیف می کنند . توجه داشته باشید که اگر C O ≠ C R زمانی که η = 0 باشد ، این عبارت سینتیکی به i loc ≠ 0 منجر می شود ، بنابراین مفهوم تعادل را نقض می کند. این ممکن است منجر به ناسازگاری ترمودینامیکی شود، به عنوان مثال هنگام جفت کردن یک مدل الکتروشیمیایی با انتقال حرارت.
ساده سازی معادله باتلر-ولمر
باتلر-ولمر خطی شده
واکنش انتقال بار را می توان با یک عبارت باتلر-ولمر خطی شده بیان کرد، که می تواند برای اضافه پتانسیل های کوچک ( η << RT/F ) استفاده شود و معمولاً به عنوان تقریب میدان کم نامیده می شود. این تقریب معادله خطی شده زیر را به دست می دهد:
معادلات آندی و کاتدی تافل
با فرض اضافه پتانسیل های آندی یا کاتدی بالا برای یک جریان معین (یعنی سینتیک آهسته یا i 0 کم )، می توان یکی از اصطلاحات پتانسیل های اولیه باتلر-ولمر را نادیده گرفت.
معادله آندی تافل به صورت زیر پیاده سازی می شود:
که در آن A ( واحد SI: V) به اصطلاح شیب تافل است. A به ضریب انتقال مربوطه به شرح زیر مربوط می شود
بیان کاتدی تافل بر اساس زیر تعریف می شود:
جایی که علامت جریان انتقال بار منفی کاتدی را به حساب می آورد. در اینجا باید A c منفی باشد و با توجه به ضریب انتقال مربوط می شود
محدود کردن چگالی جریان
سرعت حالت پایدار واکنش های الکترود هرگز نمی تواند از سرعتی که واکنش دهنده ها و محصولات می توانند به سطح الکترود و از سطح الکترود منتقل شوند بیشتر شود. هنگامی که به صراحت حمل و نقل جرم را در یک مدل شامل می شود، این وابستگی معمولاً در وابستگی به غلظت پتانسیل تعادل و چگالی جریان تبادل همانطور که در بالا توضیح داده شد، توصیف می شود.
هنگامی که به طور صریح انتقال جرم را در معادلات حوزه لحاظ نمی کنیم، باز هم می توان اثر محدودیت های انتقال را با فرض یک لایه انتشار نرنست در سطح الکترود، و یک وابستگی مرتبه اول بین جریان انتقال بار و غلظت محلی یک گونه واکنش دهنده را شامل شود. ، منجر به بیان سینتیک زیر می شود:
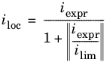
که در آن i expr (A/m 2 ) بیان چگالی جریان در غیاب محدودیتهای انتقال جرم برای گونه است و i lim (A/m 2 ) چگالی جریان محدود کننده است که با حداکثر نرخ انتقال گونه مطابقت دارد. اشتقاق این عبارت مازاد پتانسیل بالایی را در نظر می گیرد، به طوری که ممکن است عبارت آندی یا کاتدی در معادله باتلر-ولمر نادیده گرفته شود.
خطی کردن وابستگی غلظت برای غلظت های پایین
یک بیان جنبشی مبتنی بر غلظت را در نظر بگیرید
که ν و k اعداد مثبت هستند و رفتار مورد نظر این است که نرخ r و غلظت c باید در محلول همگرا در زمان بی نهایت برابر با صفر باشد. با این حال، اگر c به دلیل نوسانات عددی در فرآیند حل کننده، در حین تکرار منفی شود، ممکن است مشکلاتی ایجاد شود.
ابتدا موردی را در نظر بگیرید که ν برابر 1 (یا هر عدد صحیح مثبت فرد) باشد. مقادیر منفی c سپس باعث مثبت شدن نرخ می شود و در نتیجه وضعیت “خود تثبیت کننده” ایجاد می شود که در آن c با گذشت زمان به صفر نزدیک می شود.
مورد دومی که باید در نظر گرفت زمانی است که ν یک عدد صحیح زوج بزرگتر از 1 باشد. در این صورت نرخ برای مقادیر منفی c به طور فزاینده ای منفی می شود ، و در نتیجه یک راه حل “انفجار” ایجاد می شود که c را به سمت منهای بی نهایت تکرار می کند. راه حل استاندارد برای این موارد، که برای مقادیر ν غیر صحیح بزرگتر از 1 نیز کار می کند، تغییر عبارت c در ترم نرخ به max( c ,eps) است، جایی که eps یک عدد کوچک است. این از رفتار “انفجار” جلوگیری می کند، اما منجر به نرخ همگرایی ضعیف برای مقادیر منفی c می شود زیرا ژاکوبین نرخ نسبت به c سپس برای مقادیر منفی c صفر می شود.
حالت سوم زمانی است که ν یک عدد غیر صحیح بین 0 و 1 باشد. اکنون توجه داشته باشید که ژاکوبین با توجه به c بیان نرخ اکنون حاوی c ν-1 است، که وقتی c از سمت مثبت به صفر نزدیک شود، به منهای بی نهایت نزدیک می شود . این ممکن است منجر به همگرایی ضعیف شود، و max() wrapping باعث بهبود همگرایی در این مورد نمی شود.
راه حل مورد سوم خطی کردن وابستگی به غلظت برای غلظت های پایین است، یعنی استفاده
که منجر به رفتار همگرایی مطلوب برای غلظت های کم و منفی می شود. البته توجه داشته باشید که خطیسازی ممکن است منجر به ناسازگاریهای ترمودینامیکی شود، بهطور مثال، روابطی مانند معادله نرنست برای پتانسیل تعادل دیگر برآورده نمیشوند. خطی سازی ممکن است همگرایی مورد دوم بالا را نیز بهبود بخشد.




