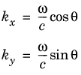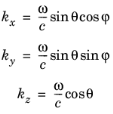چندین گزینه برای تعیین جهت اولیه پرتوها وجود دارد. این گزینه ها با تخصیص مقادیر به درجات آزادی مربوط به بردار موج k (واحد SI: راد/متر) هر پرتو کار می کنند.
پیش فرض این است که عبارتی برای بردار جهت پرتو L 0 (بدون بعد) وارد کنید. این بردار نیازی به بزرگی وحدت ندارد زیرا همیشه به طور خودکار نرمال می شود. بردار موج اولیه است
اگر موقعیتهای اولیه پرتو از یک فایل متنی بارگیری شوند، در صورت تمایل میتوان جهت اولیه پرتو را نیز از همان فایل بارگیری کرد. اگر جهت از فایل بارگذاری شده باشد و یک چرخش در موقعیت های رهاسازی اشعه اعمال شده باشد، در صورت اختیاری می توان همان چرخش را در جهت اولیه اعمال کرد.
هنگامی که Spherical انتخاب می شود، بردارهای موج اولیه از یک توزیع در فضای بردار موج در هر نقطه رهاسازی نمونه برداری می شوند. تعداد پرتوهای آزاد شده از هر نقطه معمولاً برابر با مقدار مشخص شده Nw (بدون بعد) است، اگرچه اگر مقادیر اولیه هر متغیر وابسته کمکی نیز از یک توزیع نمونه برداری شود، ممکن است بزرگتر باشد .
جایی که θ از 0 تا 2 π در مراحل N w می رود. در سه بعدی اجزای بردار موج اولیه با توجه به عبارات نمونه برداری می شوند
زاویه آزیموتال ϕ به طور یکنواخت از 0 تا 2 π توزیع شده است . زاویه قطبی θ از بازه [0, π ] با چگالی احتمال متناسب با sin θ نمونه برداری می شود . زاویه قطبی به طور دلخواه به عنوان زاویه ای انتخاب می شود که بردار موج اولیه با محور z مثبت ایجاد می کند ، اما هر جهتی را می توان انتخاب کرد زیرا کره همسانگرد است. بنابراین، هر پرتو تقریباً همان زاویه جامد را در فضای بردار موج تحت تأثیر قرار می دهد.
گزینه نیمکره مانند گزینه کروی است ، با این تفاوت که در 2 بعدی θ از 0 به π و در 3 بعدی θ از 0 به π /2 می رود . زاویه از جهت داده شده توسط تنظیم محور نیمکره اندازه گیری می شود .
گزینه Conical همانند گزینه Spherical است ، با این تفاوت که θ از 0 به α می رود . زاویه از جهت داده شده توسط تنظیم محور مخروطی اندازه گیری می شود .
گزینه Lambertian پرتوها را در یک نیمکره به صورت سه بعدی منتشر می کند، اما تابع توزیع احتمال با گزینه نیمکره متفاوت است . به یاد بیاورید که برای توزیع نیمکره ای همسانگرد، زاویه قطبی θ چگالی احتمالی متناسب با sin θ دارد . برای توزیع لامبرتی، چگالی احتمال در عوض با sin θ cos θ متناسب است . به دلیل این عبارت کسینوس اضافی، گفته میشود که توزیعهایی که از این چگالی احتمال پیروی میکنند از قانون کسینوس لامبرت پیروی میکنند.