و از طریق رابطه زیر به انتشارات چند جزئی ماکسول-استفان، D ik ، مرتبط هستند ( مرجع 2 )
(6-46)  ،
،
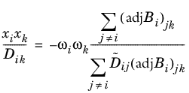 ،
،که در آن (adj B i ) jk jk امین مؤلفه از الحاق ماتریس B i است .
برای مخلوطهای گازی با چگالی کم، انتشار چند جزئی ماکسول-استفان، D ij ، میتواند با انتشار دوتایی برای جفت گونههای موجود جایگزین شود.
حل معادله 6-46 منجر به تعدادی عبارات جبری برای هر یک از اجزای ماتریس انتشار چند جزئی فیک می شود. برای سیستم های دو و سه جزئی، اینها به طور مستقیم توسط COMSOL Multiphysics پیاده سازی و حل می شوند. برای مثال، مؤلفه  در یک سیستم سه تایی به وسیله:
در یک سیستم سه تایی به وسیله:
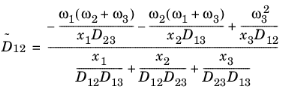
برای چهار جزء یا بیشتر، COMSOL Multiphysics انتشار فیک چند جزئی را به صورت عددی از طریق وارونگی ماتریس به دست میآورد که از ویژگیهای ماتریس تعریف شده در Ref. 2 . این برنامه با ماتریس انتشار چند جزئی Maxwell-Stefan D ik برای محاسبه ماتریس انتشار چند جزئی Fick،  با استفاده از معادله زیر شروع می شود:
با استفاده از معادله زیر شروع می شود:
(6-47)
که در آن ij شاخص هایی در ماتریس ها  و N هستند و از 1 تا تعداد گونه ها، Q متغیر است .
و N هستند و از 1 تا تعداد گونه ها، Q متغیر است .
عناصر ماتریس N در معادله 6-47 به صورت تعریف شده اند
(6-48)
که در آن P – 1 معکوس یک ماتریس P است که به صورت تعریف شده است
ماتریس  به نوبه خود به صورت تعریف شده است
به نوبه خود به صورت تعریف شده است
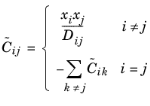
عبارت g در معادله 6-47 یک مقدار اسکالر است که ثبات عددی را فراهم می کند و باید از همان مرتبه بزرگی با ضرایب انتشار چند جزئی ماکسول-استفان باشد. بنابراین رابط فیزیک q را به عنوان مجموع ضرایب انتشار چند جزئی ماکسول-استفان تعریف می کند:
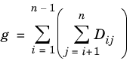
این تعریف برای g در بیشتر موارد به خوبی جواب می دهد. در موارد نادر، ممکن است نیاز به تغییر مقدار برای به دست آوردن همگرایی باشد. |
از آنجا که ماتریس انتشار فیک چند جزئی متقارن است، کافی است معادله 6-48 را برای عناصر مثلث بالایی اعمال کنیم  . عناصر باقی مانده با تعویض شاخص ها در ماتریس به دست می آیند.
. عناصر باقی مانده با تعویض شاخص ها در ماتریس به دست می آیند.




