برای اغتشاشات کوچک حول راه حل حالت پایدار، متغیرهای وابسته و منابع را می توان به شکل زیر فرض کرد:
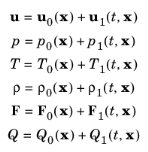
که در آن متغیرهای زیرنویس “1” نشان دهنده اغتشاشات صوتی (اغتشاش مرتبه اول) و زیرنویس “0” مقادیر میانگین جریان پس زمینه است. با فرض صفر میانگین جریان u 0 = 0 و پس از درج در معادله حاکم 6-4 ، معادلات حالت پایدار را می توان از سیستم کم کرد، که متعاقباً با نادیده گرفتن عبارت درجه دوم در متغیرهای صوتی، به مرتبه اول خطی می شود. با حذف زیرنویس “1” برای خوانایی، معادلات صوتی ترموویسکوز به دست می آید:
(6-5)
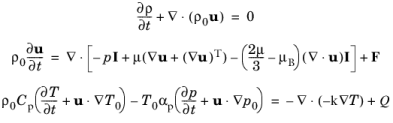
که در آن متغیرهای پرایم نشده اکنون انحراف صوتی از حالت پایدار هستند.
چگالی ρ بر حسب فشار و تغییرات دما با استفاده از دیفرانسیل چگالی بیان میشود (بسط تیلور در مورد مقادیر ساکن ثابت)
(6-6)
دو کمیت ترمودینامیکی (اصطلاح ضریب در براکتهای مربع) ضریب همبار انبساط حرارتی α p (گاهی اوقات α 0 نامیده میشود ) و تراکمپذیری همدما βT را با توجه به روابط زیر تعریف میکنند.
(6-7)
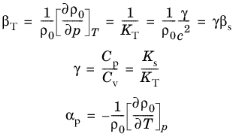
که در آن Ks مدول توده ای همتروپیک (گاهی اوقات K 0 نامیده می شود )، KT مدول حجمی همدما، Cv ظرفیت گرمایی در حجم ثابت (در واحد جرم)، c سرعت (ایسنتروپیک) صوت است، و γ است . نسبت گرمای ویژه (شاخص آدیاباتیک). تراکم همدما β T به تراکم پذیری ایزنتروپیک (یا آدیاباتیک) β s (گاهی اوقات β 0 نامیده می شود ) و ضریب انبساط حرارتی α p از طریق روابط ترمودینامیکی مربوط می شود.
(6-8)
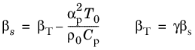
با استفاده از روابط ماکسول مشتق شده است. به عنوان مثال Ref. 5 و رفر. 7 .
از معادله 6-7 و معادله 6-8 ، تراکم پذیری همدما و ضریب انبساط حرارتی همدما را می توان بر حسب سرعت صوت به صورت بیان کرد.
(6-9)
معادلات ارائه شده در معادله 6-5 و معادله 6-6 آنهایی هستند که در حوزه زمان در Thermoviscous Acoustics, Transient Interface حل شده اند . با فرض نوسانات هارمونیک کوچک در مورد یک راه حل حالت پایدار، متغیرهای وابسته و منابع را می توان به شکل زیر فرض کرد.
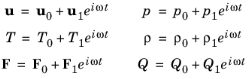
با وارد کردن این مورد در معادلات حاکم و انجام خطیسازی معادلات حل شده در حوزه فرکانس در Thermoviscous Acoustics, Frequency Domain Interface :
(6-10)
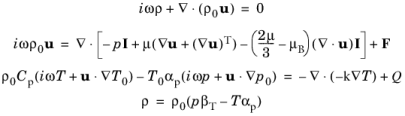
سیستم معادلات پیادهسازی شده در رابطهای صوتی ترموویسکوز بیشتر در فرمول میدان پراکنده ارائه شده است، همانطور که در زیر در فرمولاسیون میدان پراکنده و میدانهای صوتی پسزمینه توضیح داده شده است .
هنگامی که گزینه فرمول آدیاباتیک در قسمت تنظیمات معادله صوتی ترموویسکوز وجود دارد ، معادلات حل شده به زیر کاهش می یابد:
(6-11)
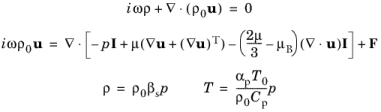
که در آن دمای T به طور مستقیم به فشار صوتی p بستگی دارد .
گاز ایده آل
برای یک گاز ایده آل، معادله حالت p = ρ RT ، که در آن R ثابت گاز خاص است، منجر به
و تراکم
با درج این عبارات و تقسیم معادله تداوم بر چگالی مرجع، معادله 6-10 در حوزه فرکانس به شکل ساده شده زیر است.
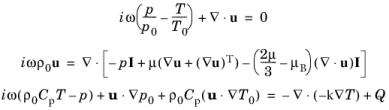
این، برای مثال، سیستم معادلات است که در هنگام انتخاب قانون گاز ایدهآل در رابط صوتی ترموویسکوز، دامنه فرکانس پیادهسازی میشود.
مورد گاز ایده آل ایزنتروپیک (آدیاباتیک).
اگر فرآیند آدیاباتیک و برگشت پذیر فرض شود – یعنی ایزنتروپیک – هدایت حرارتی به طور موثر صفر است. سپس دما را نیز می توان حذف کرد و برای مورد گاز ایده آل:
(6-12)
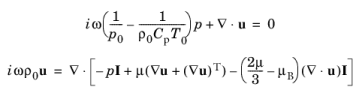
که در آن ویژگی های پس زمینه ثابت را در نظر گرفته ایم. با تعریف سرعت صوت c در قیاس با مفروضات استاندارد آکوستیک خطی (جمله مقابل فشار در معادله پیوستگی)، مشخص می شود که
یا
در مورد یک سیال عمومی، رابطه مربوطه با استفاده از معادله 6-7 و معادله 6-8 است :
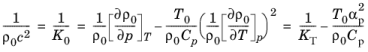
که در آن K 0 مدول حجیم آدیاباتیک، KT مدول حجمی همدما، و α 0 ضریب انبساط حرارتی است .
مورد ایزوترمال
از طرف دیگر، اگر رسانایی حرارتی بالا باشد، یا امواج صوتی ترموویسکوز در فضای باریکی بین دیوارهای بسیار رسانا منتشر شوند، می توان دما را ثابت فرض کرد (فرض همدما) و سیستم معادلات برای یک گاز ایده آل تبدیل می شود. :
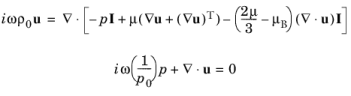
که باز هم در مقایسه با مفروضات استاندارد، به دست می دهد
یا معادل آن
بنابراین، هدایت حرارتی و/یا دیوارهای رسانا سرعت ظاهری صوت را در حوزههای باریک کاهش میدهند.
معادله هلمهولتز
اگر فرآیندهای ترمودینامیکی در سیستم را آدیاباتیک فرض کنیم و ویسکوزیته را می توان نادیده گرفت، معادله 6-12 ، برای خواص پس زمینه ثابت، به
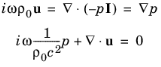
حال، با در نظر گرفتن واگرایی معادلات تکانه و درج عبارت واگرایی سرعت، برگرفته از معادلات پیوستگی، معادله هلمهولتز برای خواص ثابت مواد به دست میآید:




