آکوستیک فشار، واسط دامنه فرکانس برای چندین نوع مطالعه وجود دارد. در اینجا معادلات برای مطالعات حوزه فرکانس، فرکانس ویژه و تحلیل حالت ارائه شده است. تمام رابط ها فشار صوتی p را حل می کنند . این در همه ابعاد فضایی موجود است – برای هندسه های دکارتی 3 بعدی، 2 بعدی و 1 بعدی و همچنین برای هندسه های متقارن محوری 2 بعدی و 1 بعدی.
دامنه بسامد
فرمول حوزه فرکانس یا فرمول هارمونیک زمان از معادله هلمهولتز ناهمگن استفاده می کند:
(2-16)
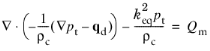
این معادله 2-14 است که با معرفی عدد موج k eq استفاده شده در معادلات تکرار می شود. این شامل هر دو عدد موج معمولی k و همچنین سهم های خارج از صفحه و آزیموتالی (یا محیطی) در صورت لزوم است. همچنین توجه داشته باشید که فشار در اینجا فشار کل p t است که مجموع یک میدان فشار زمینه احتمالی pb و میدان پراکنده ps است . این امکان را برای فرمول به اصطلاح میدان پراکنده معادلات فراهم می کند. اگر فیلد پس زمینه وجود نداشته باشد p t = p s = p .
در این معادله، p = p ( x , ω ) = p ( x )e i ω t ( وابستگی به ω از این پس به صراحت نشان داده نمی شود ). پاسخ فرکانسی را با انجام یک جاروی پارامتریک در یک محدوده فرکانس با استفاده از بارها و منابع هارمونیک محاسبه کنید.
هنگامی که میرایی وجود دارد، ρc و cc کمیت های با ارزش پیچیده هستند . مدلهای میرایی موجود و نحوه اعمال آنها در بخشهای آکوستیک فشار و تئوری برای مدلهای سیال معادل توضیح داده شده است .
معادله 2-16 معادله ای است که نرم افزار برای هندسه های سه بعدی حل می کند. در موارد کمبعد و متقارن محور، محدودیتهای وابستگی مختصات به این معنی است که معادلات از حالتی به حالت دیگر متفاوت است. در اینجا خلاصه ای از وضعیت موجود است.
2d
در دو بعدی فشار به شکلی است
که در معادله 2-16 درج شده است
(2-17)
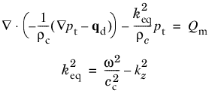
عدد موج خارج از صفحه k z را می توان در صفحه فشار آکوستیک تنظیم کرد. به طور پیش فرض مقدار آن 0 است. در مطالعه تحلیل حالت – ik z به عنوان مقدار ویژه λ استفاده می شود .
تقارن محوری دو بعدی
برای هندسه های متقارن محوری دوبعدی، متغیرهای مستقل مختصات شعاعی r و مختصات محوری z هستند . تنها وابستگی مجاز به مختصات ازیموتال  از طریق فاکتور فاز است.
از طریق فاکتور فاز است.
(2-18)
که در آن m عدد حالت آزیموتال را نشان می دهد . شماره مد یک عدد موج آزیموتال k m = m / r را تعریف می کند . از آنجا که مختصات ازیموتال تناوبی است، m باید یک عدد صحیح باشد. درست مانند k z در حالت دو بعدی، m را می توان در پنجره تنظیمات برای آکوستیک فشار تنظیم کرد.
در نتیجه معادله 2-18 ، معادله حل فشار صوتی در هندسه متقارن محوری دوبعدی تبدیل می شود.
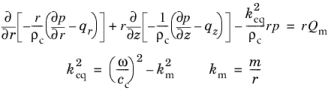
تقارن محوری 1 بعدی
در هندسه متقارن محوری یک بعدی،
منتهی به معادله شعاعی
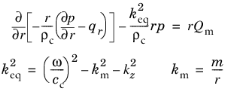
که در آن هر دو عدد موج آزیموتال k m و عدد موج محوری k z به عنوان پارامتر ظاهر می شوند.
1D
معادله مورد 1D با وابستگی فشار به یک مختصات دکارتی x به دست می آید :
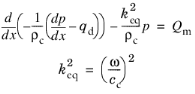
فرکانس خود
در فرمول فرکانس ویژه، اصطلاحات منبع وجود ندارند. حالت های ویژه و فرکانس های ویژه برای:
(2-19)
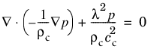
مقدار ویژه λ معرفی شده در این معادله به فرکانس ویژه f و فرکانس زاویه ای ω ، از طریق λ = i 2 π f = i ω مربوط می شود . از آنجا که آنها مستقل از فشار هستند، حل کننده هر منبع دوقطبی و تک قطبی را نادیده می گیرد، مگر اینکه یک مشکل ارزش ویژه جفت شده حل شود.
معادله 2-19 در مورد 3 بعدی اعمال می شود. معادلات حل شده در مطالعات فرکانس ویژه در ابعاد پایینتر و برای هندسههای متقارن محور، از همتایان هماهنگ زمانی آنها، که در بخش فرعی قبلی، باجایگزینی ω2 → -λ2 به دست آمدهاند .
با انتخاب از لیست تبدیل مقدار ویژه در پنجره تنظیمات دنباله حل کننده برای مقدار ویژه، بین تعیین مقادیر ویژه، فرکانس های ویژه و فرکانس های زاویه ای جابجا شوید.
ارتعاشات یک دیسک که توسط یک سیلندر پر از هوا پشتیبانی می شود : مسیر کتابخانه برنامه Acoustics_Module/Verification_Examples/coupled_vibrations |
تجزیه و تحلیل حالت در دو بعدی و متقارن محوری 1 بعدی
به مطالعه تحلیل حالت در بخش آکوستیک فشار، معادلات حالت مرزی مراجعه کنید . نوع مطالعه تحلیل حالت فقط برای رابط آکوستیک فشار، دامنه فرکانس در مولفههای متقارن محوری دوبعدی و یک بعدی موجود است، جایی که حلکننده مقادیر ویژه λ = – ik z را برای فرکانس معین حل میکند. در اینجا kz عدد موج خارج از صفحه یک حالت معین است و میدان فشار حاصل p نشان دهنده حالت در مقطع یک موجبر یا مجرای بی نهایت است .




