قانون آمپر به صورت نوشته شده است
(2-9)
جریان کل توسط
(2-10)
جایی که
جریان القایی است،
جابجایی الکتریکی در حد فرکانس بالا است (به این معنا که مدت زمان تحریک کمتر از کوتاهترین زمان شل شدن شارژ است).
شل شدن شارژ با استفاده از جریان پلاریزاسیون مدل سازی شده است ( مرجع 1 )
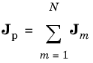
که در آن هر عبارت از معادله ای به شکل زیر تبعیت می کند:
(2-11)
که در آن τ m زمان آرامش است و Δε m سهم نسبی گذردهی است. توجه داشته باشید که هر دو کمیت را می توان به عنوان ماتریس های مورب برای پوشش حالت ناهمسانگرد در نظر گرفت.
معرفی متغیرهای جدید، میدان الکتریکی کمکی از
معادله 2-11 را می توان یک بار با توجه به زمان با فرض صفر فیلدهای اولیه ادغام کرد
(2-12)
جریان پلاریزاسیون را می توان به صورت هر دو بیان کرد
(2-13)
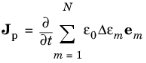
یا
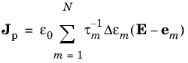
با اعمال عملگر واگرایی، معادله 2-9 معادله بقای فعلی را به دست می دهد:
فرض کنید که رسانایی الکتریکی کوچک است، به طوری که می توان جریان القایی را نادیده گرفت. با استفاده از معادله 2-13 ، معادله بقای فعلی را می توان به صورت نوشتاری نوشت
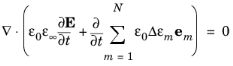
که می تواند یک بار با توجه به زمان با فرض صفر بودن میدان های اولیه ادغام شود تا معادله بقای بار به دست آید.
(2-14)
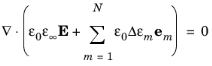
معادله 2-14 را می توان با استفاده از پتانسیل الکتریکی اسکالر V به عنوان یک متغیر وابسته حل کردکه میدان الکتریکی را به عنوان تعیین می کند ، و باید همراه با N بردار معادله 2-12 برای N متغیرهای بردار وابسته e m حل شود . در حوزه زمان، این متغیرهای میدان کمکی را می توان به عنوان متغیرهای حالت محلی در نظر گرفت و هر یک از N معادله ODE مربوطه را می توان به صورت محلی ادغام کرد.
، و باید همراه با N بردار معادله 2-12 برای N متغیرهای بردار وابسته e m حل شود . در حوزه زمان، این متغیرهای میدان کمکی را می توان به عنوان متغیرهای حالت محلی در نظر گرفت و هر یک از N معادله ODE مربوطه را می توان به صورت محلی ادغام کرد.
دامنه بسامد
در حوزه فرکانس، معادله 2-13 برای متغیرهای کمکی را می توان به صورت تحلیلی حل کرد، به طوری که معادله 2-14 به دست می دهد .
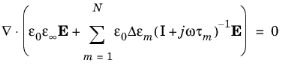
که در آن ω فرکانس زاویه ای است. با جدا کردن بخش های واقعی و خیالی، می توان معادله را بازنویسی کرد
جایی که
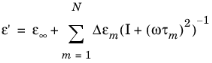
و
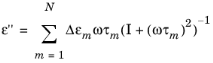
هر جمله در مجموع معادلات بالا نشان دهنده یک قطب در صفحه مختلط w است. بنابراین، این مدل به عنوان مدل پراکندگی چند قطبی Debye نامیده می شود. تعیین تعداد قطب های مورد نیاز برای تقریب رفتار مواد با اتلاف می تواند کار دشواری باشد. یک رویکرد ممکن در بخش مماس تلفات ثابت ارائه شده است .
مطالعه فرکانس ویژه
استفاده مستقیم از گذردهی پیچیده وابسته به فرکانس منجر به یک مسئله ارزش ویژه غیرخطی می شود، که راه حل آن به نقطه خطی شدن مقدار ویژه (فرکانس نقطه تبدیل، مشخص شده در حل کننده) بستگی دارد. راه حل فقط برای فرکانس ویژه ای که نزدیک به فرکانس نقطه تبدیل است دقیق است. بنابراین، فرکانسهای ویژه باید یک به یک با استفاده از بهروزرسانیهای تکراری مقدار فرکانس نقطه تبدیل محاسبه شوند.
در عوض، می توان N معادله جبری را برای متغیرهای کمکی e m حل کرد
(2-15)
همراه با معادله 2-15 . حتی اگر این رویکرد به درجات آزادی بیشتری نیاز دارد، سهم مستقل فرکانسی در ماتریسهای میرایی و سختی ایجاد میکند. مسئله مقدار ویژه میرایی خطی مربوطه را می توان با استفاده از حل کننده پیش فرض در یک اجرا برای هر تعداد مشخصی از فرکانس های ویژه که دقیقاً محاسبه می شود حل کرد.
در عمل، تجزیه و تحلیل فرکانس ویژه تنها زمانی معنا پیدا میکند که رابط الکترواستاتیک همراه با برخی فیزیکهای دیگر که یک ماتریس جرم مناسب را تعریف میکنند، استفاده شود. به عنوان مثال، یک مدل چندفیزیکی که شامل مکانیک جامدات (یا سایر رابطهای ساختاری موجود در ماژول مکانیک سازهای) است. یکی دیگر از احتمالات، اتصال بین رابط الکترواستاتیک و مدارهای الکتریکی است. |
مماس تلفات ثابت
در حوزه فرکانس، مماس تلفات به صورت تعریف می شود
(2-16)
و اغلب برای توصیف مواد با اتلاف بر اساس داده های تجربی استفاده می شود.
در Ref. 2 ، یک پارامتر ویژه برای مدل چند قطبی Debye بر اساس نتیجه اصلی مشتق شده در Ref پیشنهاد شد. 3 برای مدارهای الکتریکی معادل. این اجازه می دهد تا پارامترهای مدل را برای مدل چند قطبی دبای تناسب دهیم به طوری که مماس تلفات در یک محدوده فرکانسی مشخص تقریباً ثابت باشد.
پارامترهای ورودی عبارتند از مماس تلفات η ( fc ) همراه با فرکانس مرکزی fc ، که در آن اندازه گیری شده است، و پهنای باند مدل n d که یک بازه فرکانسی (در دهه ها) با مرکز fc را تعریف می کند ، که در آن مماس تلفات تقریباً ثابت و برابر η ( fc ) خواهد بود .
زمانهای آرامش به صورت محاسبه میشوند  ، جایی که فرکانسهای مربوطه در فضای لگاریتمی بهطور مساوی فاصله دارند.
، جایی که فرکانسهای مربوطه در فضای لگاریتمی بهطور مساوی فاصله دارند.
که در آن N تعداد قطب های Debye است و  .
.
سهم مجوز نسبی مربوطه توسط داده می شود
که در آن k > 1 پارامتر فاصله است. توجه داشته باشید که گذردهی نسبی الکتریکی در محدوده فرکانس پایین و بالا به سادگی به صورت  .
.
نرم افزار COMSOL Multiphysics به طور خودکار تعداد لازم قطب N را به همراه مقادیر زمان آرامش tm و سهم گذردهی نسبی Δεm استنباط می کند ، که در محاسبات برای حفظ پهنای باند و دقت درخواستی استفاده می شود.
دقت را می توان برای دادن به صورت عادی انتخاب کرد
برای
که به قطب نیاز دارد 
 و پارامتر فاصله با زاویه افت d از η ( fc ) محاسبه می شود.
و پارامتر فاصله با زاویه افت d از η ( fc ) محاسبه می شود.
به طور متناوب، دقت را می توان برای به دست آوردن بالا انتخاب کرد
در همان بازه زمانی که به  قطب ها نیاز دارد و پارامتر فاصله
قطب ها نیاز دارد و پارامتر فاصله  .
.
بنابراین پارامترهای محاسبه شده به طور خودکار در یک مطالعه وابسته به زمان با استفاده از معادله 2-12 و در یک مطالعه فرکانس ویژه با استفاده از معادله 2-16 استفاده خواهند شد .
در مطالعه فرکانس ویژه و مطالعه وابسته به زمان، هر قطب به یک درجه آزادی بردار اضافی (متغیر دامنه) نیاز دارد تا سهم مربوط به قطبش را نشان دهد. بنابراین، استفاده از قطب های زیاد در داده های آرامش، یا انتخاب دقت بالا n مورد مماس تلفات ثابت، می تواند به هزینه های محاسباتی قابل توجهی برای مدل های بزرگتر منجر شود. |
اثرات دما
برای بسیاری از مواد دی الکتریک مانند پلیمرها، خواص شل شدن بار بستگی زیادی به دما دارد. یک فرض رایج این است که تغییر در دما می تواند مستقیماً به تغییر در مقیاس زمانی تبدیل شود. زمان کاهش یافته به این صورت تعریف می شود
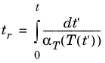
که در آن α T ( T ) یک تابع تغییر وابسته به دما است.
مفهوم این است که مشکل را می توان با استفاده از داده های ماده اصلی حل کرد، مشروط بر اینکه زمان به زمان کاهش یافته تبدیل شود. تابع تغییر α T ( T ) را به عنوان ضریب زمان استراحت در معادله 2-12 و معادله 2-16 در نظر بگیرید .
شیفت فوگل-فولچر
تابع shift توسط
در اینجا، یک لگاریتم پایه-e استفاده می شود، Q انرژی فعال سازی است (واحد SI: J/mol)، و R ثابت گاز جهانی است. دمای T 0 دمایی است که در آن زمان آرامش بی نهایت می شود.
آرنیوس شیفت
تابع shift از قانون آرنیوس پیروی می کند
در اینجا، یک لگاریتم پایه-e استفاده می شود، Q انرژی فعال سازی است (واحد SI: J/mol)، و R ثابت گاز جهانی است.
شیفت ویلیامز-لندل-فری
یکی از تابعهای شیفت رایج با معادله WLF (ویلیامز-لندل-فری) تعریف میشود:
که در آن از لگاریتم پایه 10 استفاده شده است. این تغییر فقط در یک محدوده دمایی خاص، معمولاً در حدود دمای انتقال شیشه ای معتبر است.
اولین گام برای محاسبه تابع تغییر αT ( T ) شامل ساخت منحنی اصلی بر اساس داده های تجربی است . برای انجام این کار، منحنی های خواص دی الکتریک در برابر زمان یا فرکانس در دمای مرجع T ref اندازه گیری می شوند . سپس، همان خواص در دماهای مختلف اندازه گیری می شود.
مقدار تغییر هر منحنی، با توجه به منحنی اصلی به دست آمده در دمای T ref ، ضریب تغییر αT ( T ) را تعریف می کند. ثابت های C 1 و C 2 وابسته به ماده هستند و پس از رسم log ( αT ) در مقابل T – T ref محاسبه می شوند .
ضریب تغییر در دمای مرجع برابر با α T ( T ref ) = 1 است، به طوری که T ref دمایی است که در آن منحنی اصلی داده می شود. اگر دمای T به زیر T ref – C 2 کاهش یابد ، معادله WLF دیگر معتبر نیست. |
از آنجایی که منحنی اصلی در یک دمای مرجع دلخواه T ref اندازهگیری میشود ، ضریب تغییر αT ( T ) را میتوان با توجه به هر دما به دست آورد و معمولاً به عنوان تغییر با توجه به دمای انتقال شیشهای در نظر گرفته میشود .
Tool–Narayanaswamy–Moynihan Shift
شل شدن شارژ در شیشه را می توان با استفاده از ضریب شیفت Tool-Narayanaswamy-Moynihan مدل کرد که به صورت داده شده است.
در اینجا، یک لگاریتم پایه-e استفاده می شود، Q انرژی فعال سازی است (واحد SI: J/mol)، R ثابت گاز جهانی، T دمای فعلی، T ref یک دمای مرجع، χ انرژی فعال سازی بدون بعد است. کسر، و T f به اصطلاح دمای خیالی است. دمای فرضی به عنوان میانگین وزنی دماهای فرضی جزئی داده می شود.
در اینجا w i وزن ها و T fi دماهای خیالی جزئی هستند. دماهای خیالی جزئی از یک سیستم معادلات دیفرانسیل معمولی جفت شده (ODEs) که از معادله Tool پیروی می کنند تعیین می شوند.
در اینجا، λ 0i یک پارامتر زمان آرامش است.
مراجع برای پراکندگی DEBYE
1. NS Stoykov، TA Kuiken، MM Lowery، و A. Taflove، «الگوریتمهای حوزه زمان المان محدود برای مدلسازی پراکندگیهای دیالکتریک خطی Debye و Lorentz در فرکانسهای پایین»، IEEE Transactions on Biomedical Engineering، جلد . 50، شماره 9، صص 1100-1107، 2003.
2. AE Engin، I. Ndip، K. Lang، و J. Aguirre، “مدل دبای چندقطبی شکل بسته برای مدلسازی دامنه زمانی دی الکتریکهای تلفاتی،” IEEE Trans. در مورد سازگاری الکترومغناطیسی ، جلد. 61، شماره 3، صفحات 966-968، 2019.
3. R. Morrison، “پذیرش نقاط رانندگی با استدلال ثابت،” IRE Trans. تئوری مدار ، جلد. 6، نه 3، صص 310-317، 1959.
4. JA Diego، J. Sellares، A. Aragoneses، M. Mudarra، JC Canadas، و J. Belana، “مطالعه TSDC از انتقال شیشه ای: همبستگی با داده های کالریمتری”، مجله فیزیک D: فیزیک کاربردی ، جلد. 40، صص 138-1145، 2007.




