کادر محاوره ای ویرایش قانون اختلاط برای کنترل قوانین اختلاط در جدول محتویات مواد یک ماده چند فازی یا ماده موثر استفاده می شود .
برای باز کردن کادر گفتگوی Edit mixing rule :
• | روی ردیف مورد نظر در جدول محتویات مواد کلیک راست کرده و Edit mixing rule ( |
• | یک ردیف را انتخاب کنید و روی دکمه Edit mixing rule ( |
اگر چندین ویژگی ماده در جدول وجود دارد، میتوانید بدون بستن دیالوگ با استفاده از ردیف قبلی (صرفنظر کردن تغییرات) (  )، ردیف قبلی (ذخیره تغییرات) (
)، ردیف قبلی (ذخیره تغییرات) (  )، ردیف بعدی (صرفکردن تغییرات) (
)، ردیف بعدی (صرفکردن تغییرات) (  ) و دکمه های نوار ابزار ردیف بعدی (تغییرهای ذخیره) (
) و دکمه های نوار ابزار ردیف بعدی (تغییرهای ذخیره) (  ). ردیف فعلی با فیلدهای Property Group و Parameter مشخص می شود .
). ردیف فعلی با فیلدهای Property Group و Parameter مشخص می شود .
مواد چند فازی و موثر از چندین قانون اختلاط مختلف پشتیبانی می کنند. برخی از قوانین فقط برای پارامترهای مواد خاص در دسترس هستند. قوانین اختلاط برای کامپوزیت ها منحصر به ماده موثر است و ویسکوزیته نوع کریگر فقط برای مواد چند فازی موجود است.
قوانین اصلی اختلاط
قوانین اختلاط اولیه برای همه خواص مواد در دسترس است.
میانگین حجم
قانون اختلاط میانگین حجمی از یک میانگین حسابی وزن شده توسط کسرهای حجمی استفاده می کند.
(2-1)
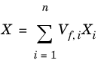
که در آن n تعداد فازها است، Vf , i کسر حجمی فاز i است ، X خاصیت ماده موثر و Xi خاصیت مادی فاز i است .
میانگین جرم
قانون اختلاط میانگین جرمی از میانگین حسابی استفاده می کند که با کسرهای جرمی وزن شده است.
(2-2)
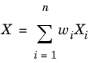
جایی که w i کسر جرمی فاز i است ،
(2-3)
در اینجا ρ چگالی موثر و ρ i چگالی فاز i است .
قانون اختلاط میانگین جرمی برای چگالی موجود نیست.
میانگین حجم هارمونیک
قانون اختلاط متوسط حجم هارمونیک از یک میانگین هارمونیک وزن شده توسط کسرهای حجمی استفاده می کند.
(2-4)
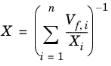
میانگین جرم هارمونیک
قانون اختلاط میانگین جرم هارمونیک از یک میانگین هارمونیک وزن شده توسط کسرهای جرمی استفاده می کند.
(2-5)
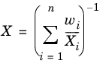
قانون اختلاط میانگین جرم هارمونیک برای چگالی موجود نیست.
قانون قدرت
قانون اختلاط قانون توان از توزیع قانون توان استفاده می کند.
(2-6)
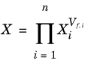
تابع Heaviside
قانون اختلاط تابع Heaviside از یک میانگین حسابی استفاده می کند که با یک تابع گام صاف از کسر حجمی وزن شده است:
(2-7)
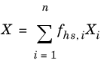
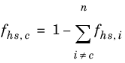
قوانین اختلاط برای مواد کامپوزیت
خواص ساختاری موثر مواد کامپوزیت به خواص مواد تشکیل دهنده و آرایش هندسی آنها بستگی دارد. اینها را می توان به صورت تحلیلی یا عددی تقریبی کرد. روش عددی برای طیف وسیع تری از پیکربندی های هندسی قابل استفاده است، اما استفاده از آن پیچیده تر است. ماده موثر شامل فهرستی از رویکردهای تحلیلی است که ساده و مفید هستند، با هدف مواردی که فیبر ارتوتروپیک به عنوان تقویت کننده یک ماتریس همسانگرد عمل می کند. این روش ها از Ref. 1 ، ر. 2 و رفر. 3 .
در این بخش، ویژگی های تقویت کننده های الیاف با زیرنویس f نشان داده می شود ، در حالی که خواص ماتریس با m نشان داده می شود . قوانین اختلاط برای کامپوزیت ها فقط برای مجموعه خاصی از خواص مواد موجود است. این قوانین باید همراه با قانون اختلاط میانگین حجم برای چگالی استفاده شوند.
مدل Voigt-Reuss
مدل Voigt-Reuss، همچنین به عنوان قانون مخلوط شناخته می شود، یک روش تحلیلی برای محاسبه خواص مواد همگن کامپوزیت ها است. این روش برای مواردی که فیبرهای ارتوتروپیک پیوسته در ماتریس همسانگرد تعبیه شده اند، به خوبی کار می کند.
پارامتر مواد | گروه اموال | جزء | خاصیت ترکیبی موثر |
مدول یانگ، E | ارتوتروپیک | E 11 | |
E22 _ | |||
E 33 | |||
نرخ برش، G | ارتوتروپیک | G 12 | |
G23 _ | |||
G 13 | |||
نسبت پواسون، ν | ارتوتروپیک | n 12 | |
n 23 | |||
n 13 | |||
ضریب انبساط حرارتی، α | یک 11 | ||
یک 22 | |||
یک 33 | |||
ضریب تورم هیگروسکوپیک، β | ب 11 | ||
ب 22 | |||
ب 33 | |||
هدایت حرارتی، k | پایه ای | k 11 | |
k22 _ | |||
k 33 | |||
هدایت الکتریکی، σ | پایه ای | ص 11 | |
ص 22 | |||
ص 33 |
مدل اصلاح شده Voigt–Reuss
مدل Voigt-Reuss نتایجی را در جهتهای طولی ارائه میدهد که مطابقت خوبی با آزمایشها دارند، اما نه در جهتهای عرضی. مدل اصلاح شده Voigt-Reuss یا قانون اصلاح شده مخلوط، اصلاحاتی را در جهت عرضی ارائه می دهد. عوامل تصحیح زیر استفاده می شود:
(2-8)
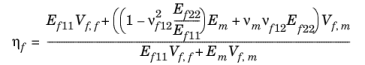
(2-9)
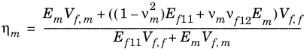
(2-10)
پارامتر مواد | گروه اموال | جزء | خاصیت ترکیبی موثر |
مدول یانگ، E | ارتوتروپیک | E 11 | |
E22 _ | |||
E 33 | |||
نرخ برش، G | ارتوتروپیک | G 12 | |
G23 _ | |||
G 13 | |||
نسبت پواسون، ν | ارتوتروپیک | n 12 | |
n 23 | |||
n 13 |
مدل Chamis
مدل Chamis برای الیاف orthotropic پیوسته تعبیه شده در ماتریس همسانگرد به خوبی کار می کند. برخلاف مدل Voigt-Reuss، می توان از آن برای الیاف یک طرفه پراکنده تصادفی استفاده کرد.
پارامتر مواد | گروه اموال | جزء | خاصیت ترکیبی موثر |
مدول یانگ، E | ارتوتروپیک | E 11 | |
E22 _ | 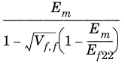 | ||
E 33 | 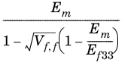 | ||
نرخ برش، G | ارتوتروپیک | G 12 | 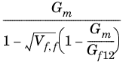 |
G23 _ | 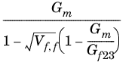 | ||
G 13 | 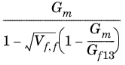 | ||
نسبت پواسون، ν | ارتوتروپیک | n 12 | |
n 23 | |||
n 13 | |||
ضریب انبساط حرارتی، α | یک 11 | ||
یک 22 | 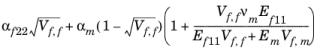 | ||
یک 33 | 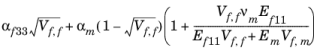 | ||
ضریب تورم هیگروسکوپیک، β | ب 11 | ||
ب 22 | 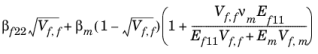 | ||
ب 33 | 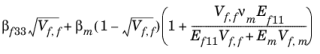 | ||
هدایت حرارتی، k | پایه ای | k 11 | |
k22 _ | 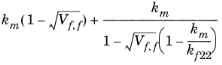 | ||
k 33 | 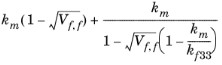 |
مدل Halpin–Tsai
مدل Halpin-Tsai یک روش نیمه تجربی برای محاسبه خواص همگن کامپوزیت ها بر اساس میکرومکانیک خودسازگار و همچنین برازش منحنی تجربی است. این روش برای الیاف ارتوتروپیک پیوسته یا الیاف ارتوتروپیک ناپیوسته تعبیه شده در ماتریس همسانگرد، از جمله الیاف کوتاه، به خوبی کار می کند.
مدل Halpin-Tsai شامل عوامل تجربی ζ برای اجزای مدول الاستیک است و معیاری از تقویت است که به هندسه الیاف بستگی دارد. برخی از مقادیر معمولی برای مدول یانگ orthotropic در مقدار جدول نشان داده شده است. مقدار ζ برای اجزای G معمولاً 1 است .
جزء | ζ برای الیاف ناپیوسته | ζ برای الیاف پیوسته |
E 11 | ∞ | |
E22 _ | 0 |
در جدول بالا، l 11 طول فیبر در جهت 11، w 22 عرض فیبر در جهت 22، و t 33 ضخامت فیبر در جهت 33 است.
خواص موثر مواد توسط:
پارامتر مواد | گروه اموال | جزء | خاصیت ترکیبی موثر |
مدول یانگ، E | ارتوتروپیک | E 11 | 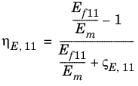 |
E22 _ | 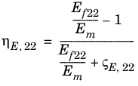 | ||
E 33 | 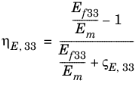 | ||
نرخ برش، G | ارتوتروپیک | G 12 | 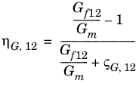 |
G23 _ | 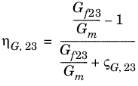 | ||
G 13 | 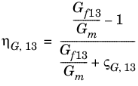 | ||
نسبت پواسون، ν | ارتوتروپیک | n 12 | |
n 23 | |||
n 13 |
مدل Halpin–Tsai–Nielsen
مدل Halpin–Tsai–Nielsen مدل Halpin–Tsai را با در نظر گرفتن حداکثر کسر بستهبندی تقویتکننده گسترش میدهد  (پیشفرض 0.82). مقادیر معمولی حداکثر فاکتور بسته بندی در جدول 2-8 فهرست شده است .
(پیشفرض 0.82). مقادیر معمولی حداکثر فاکتور بسته بندی در جدول 2-8 فهرست شده است .
چیدمان فیبر | |
آرایه مربعی از الیاف | 0.785 |
آرایه شش ضلعی از الیاف | 0.907 |
ترتیبات دیگر | 0.82 |
مدل Halpin-Tsai-Nielsen یک متغیر کمکی را معرفی می کند.
(2-11)
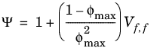
و خواص موثر در جدول 2-9 آورده شده است .
پارامتر مواد | گروه اموال | جزء | خاصیت ترکیبی موثر |
مدول یانگ، E | ارتوتروپیک | E 11 | 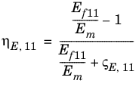 |
E22 _ | 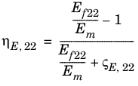 | ||
E 33 | 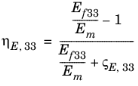 | ||
نرخ برش، G | ارتوتروپیک | G 12 | 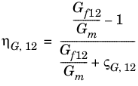 |
G23 _ | 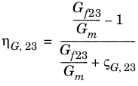 | ||
G 13 | 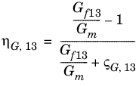 | ||
نسبت پواسون، ν | ارتوتروپیک | n 12 | |
n 23 | |||
n 13 |
مدل هاشین – روزن
مدل Hashin-Rosen بر اساس مجموعه سیلندر مرکب (CCA) است. برای محاسبه خواص مواد همگن، ابتدا خواص اضافی محاسبه می شود.
مدول حجمی فیبر Kf و ماتریس Km تحت کرنش طولی عبارتند از
(2-12)
(2-13)
مدول توده ای کامپوزیت K تحت کرنش طولی است
(2-14)
در این مدل، مدول برش موثر کامپوزیت G 23 از معادله درجه دوم تقریب زده شده است.
(2-15)
جایی که
(2-16)
(2-17)
(2-18)
و
سپس خواص مواد موثر در جدول 2-10 آورده شده است .
پارامتر مواد | گروه اموال | جزء | خاصیت ترکیبی موثر |
مدول یانگ، E | ارتوتروپیک | E 11 | 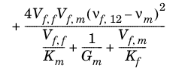 |
E22 _ | |||
E 33 | |||
نرخ برش، G | ارتوتروپیک | G 12 | |
G23 _ | ارزش مثبت از | ||
G 13 | |||
نسبت پواسون، ν | ارتوتروپیک | n 12 | 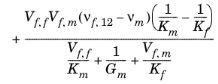 |
n 23 | 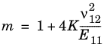 | ||
n 13 | 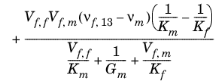 |
سایر قوانین اختلاط در مواد چند فازی
ویسکوزیته نوع کریگر
ویسکوزیته دینامیکی موثر μ در سیستم تعلیق را می توان با استفاده از مدل کریگر مدل کرد.
(2-19)
هنگامی که ویسکوزیته نوع کریگر انتخاب شد، یک مقدار یا عبارت برای حداکثر غلظت بسته بندی  (بدون ابعاد) وارد کنید. پیش فرض 0.62 است.
(بدون ابعاد) وارد کنید. پیش فرض 0.62 است.
قانون اختلاط نوع کریگر فقط برای پارامتر ویسکوزیته دینامیکی در گروه ویژگی اصلی موجود است.
مراجع برای قوانین اختلاط
1. KK Chawala، “مواد مرکب: علم و مهندسی”، Springer، 2012.
2. J. Aboudi، SM Arnold و BA Bednarcyk، “Micromechanics of Composite Materials: A Generalized Multiscale Analysis Approach”، Elsevier، 2013.
3. JC Halpin و JL Kardos، “معادلات Halpin-Tsai: A Review,” Polymer Eng. علوم پایه. ، جلد 16، شماره 5، صص 344-352، 1976.




