میدان های الکترومغناطیسی ساکن هستند اگر
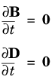
یعنی، اگر میدان ها به قدری آهسته تغییر کنند که بتوان از مشارکت جریان های القایی و جریان های جابجایی چشم پوشی کرد.
همچنین فرض کنید که اشیاء مدلسازیشده در حال حرکت با v = 0 نیستند ، بنابراین هیچ کمکی از نیروهای لورنتس وجود ندارد. اینها بعدا درمان می شوند.
تانسور استرس الکترومغناطیسی
برای اعمال تانسور تنش در هوا برای محاسبه کل نیرو و گشتاور روی یک میله قابل مغناطیسی نزدیک به آهنربای دائمی، به آهنربای دائمی : مسیر کتابخانه کاربرد ACDC_Module/Introductory_Magnetostatics/Permanent_magnet مراجعه کنید . |
عبارات تانسور تنش در یک زمینه الکترومغناطیسی عمومی از تلفیقی از نظریه مواد، ترمودینامیک، مکانیک پیوسته و نظریه میدان الکترومغناطیسی ناشی میشود. با معرفی پتانسیلهای ترمودینامیکی برای اثرات مکانیکی، حرارتی و الکترومغناطیسی، عبارات صریح برای تانسور تنش را میتوان به روشی مناسب با تشکیل مشتقات رسمی با توجه به میدانهای فیزیکی مختلف استخراج کرد (مرجع 1 و مرجع 3 ) . مشتقات جایگزین را می توان برای خلاء ایجاد کرد ( مرجع 4 ) اما نمی توان آنها را به راحتی به مواد قطبی و مغناطیسی تعمیم داد.
هوا و خلاء
برای هوا، تانسور تنش است
که در آن p فشار هوا است، I همان تانسور (یا ماتریس) 3 در 3 است، و E و B بردارهای 3 در 1 هستند. در این بیان تانسور تنش، هوا غیرقابل قطبش و غیرقابل مغناطیسی در نظر گرفته می شود. هنگامی که هوا با خلاء تقریب می شود، p = 0. این عبارت، با p = 0، تانسور تنش به عنوان تانسور تنش ماکسول نیز شناخته می شود.
با استفاده از این واقعیت که برای هوا، D = ε 0 E و B = μ 0 H بیان تانسور تنش را می توان به صورت نوشتاری
معادله موازنه نیروها می شود
معادلات ماکسول در فضای آزاد نشان می دهد که سهم بخش الکترومغناطیسی تانسور تنش صفر است و عبارت حاصل برابر است با
بنابراین، با استفاده از اصطلاحات قبلی، f em = 0 برای هوا، با σ M = – pI . در استخراج نیروی کل روی یک جامد الاستیک احاطه شده توسط خلاء یا هوا، از تقریب ∇ p = 0 استفاده شده است.
هنگام کار با عملگر واگرایی روی تانسور تنش، رابطه
مفید است (و به طور مشابه برای B ). از سمت راست مشخص است (با استفاده از معادلات ماکسول) که این عدد برای میدان های ساکن در فضای آزاد صفر است.
مجدداً مورد جامد احاطه شده توسط هوا را در نظر بگیرید. برای محاسبه نیروی کل، پیش بینی تانسور تنش در خارج از سطح جامد مورد نیاز است.
که در آن n 1 سطح نرمال است، یک بردار 1 در 3، که از جامد نشان می دهد. این عبارت را می توان مستقیماً در انتگرال مرزی تانسور تنش برای محاسبه کل نیروی F بر روی جامد استفاده کرد.
هادی خالص الاستیک
برای مثالی از نحوه محاسبه نیروی کل روی دو سیم موازی یا با ادغام نیروی حجمی یا با ادغام تانسور تنش روی سطح اطراف، به نیروهای الکترومغناطیسی روی سیمهای حامل جریان موازی مراجعه کنید : مسیر کتابخانه کاربرد ACDC_Module/Introductory_Electromagnetic_Forces/parallel . |
ماده ای که غیرقطبی و غیرقابل مغناطیسی باشد ( P = 0 و M = 0) رسانای خالص نامیده می شود . این لزوما معادل یک هادی کامل نیست که برای آن E = 0 است، بلکه صرفاً یک محدودیت در خواص دی الکتریک و مغناطیسی ماده است. تانسور تنش با تانسور هوا یکسان می شود، به جز اینکه − pI با تانسور تنش کاملاً مکانیکی σM جایگزین شود :
که در آن D = ε 0 E و B = μ 0 H .
وضعیت کمی با مورد هوا متفاوت است زیرا ممکن است جریان و بار حجمی در هادی وجود داشته باشد. چگالی جریان است
و چگالی بار حجمی
معادله موازنه نیروها اکنون تبدیل شده است
و این بدان معنی است که
مواد الاستیک عمومی
برای یک جامد الاستیک، در حالت کلی ماده ای که هم دی الکتریک و هم مغناطیسی است ( صفر و M غیرصفر )، تانسور تنش با عبارت داده می شود.
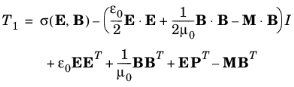
جایی که در σ ( E , B ) وابستگی E و B جدا نشده است. بنابراین σ در این حالت کلی یک تانسور تنش مکانیکی صرف نیست. مدلهای مختلف مواد ظاهری متفاوت از σ ( E ، B ) میدهند. سهم الکترومغناطیسی به σ ( E , B ) معمولاً نشان دهنده اثرات پیرو الکتریک، پیرومغناطیسی، پیزوالکتریک، پیزومغناطیسی، دی الکتریک و مغناطش است. بیان تانسور تنش در خلاء، هوا و هادی های خالص را می توان از این عبارت کلی با تنظیم M = استخراج کرد.P = 0 .
T 1 باید متقارن باشد. اصطلاحات EP T و – MB T در مورد مواد دی الکتریک و مغناطیسی خطی متقارن هستند زیرا
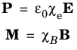
در اینجا، حساسیت مغناطیسی χ B کمی با χ m کلاسیک متفاوت است . سایر اصطلاحات صریح همگی متقارن هستند، همانطور که σ است ( E ، B ). در حالت کلی، این محدودیتهایی را بر خواص σ ( E , B ) تحمیل میکند. برای یک ماده غیرخطی σ ( E , B ) ممکن است نیاز به شامل عباراتی مانند – EP T یا + MB T باشد تا EP T نامتقارن یا – MB T را جبران کند .
برای نمونه سازی تانسور تنش برای حالت الاستیک عمومی، یک مدل ماده صریح شامل اثرات مغناطیسی و قطبش مورد نیاز است. چنین مدل های موادی را می توان به راحتی برای مواد پیزوالکتریک یافت ( مراجعه 3 ).




