متغیرهای وابسته در معادلات برینکمن، سرعت و فشار دارسی هستند. جریان در محیط متخلخل توسط ترکیبی از معادله پیوستگی و معادله تکانه کنترل می شود که با هم معادلات برینکمن را تشکیل می دهند:
(7-51)
(7-52)
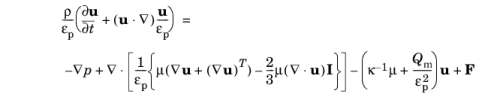
در این معادلات:
• | μ (واحد SI: kg/(m·s)) ویسکوزیته دینامیکی سیال است |
• | u (واحد SI: m/s) بردار سرعت است |
• | ρ (واحد SI: kg/m 3 ) چگالی سیال است |
• | p (واحد SI: Pa) فشار است |
• | ε p تخلخل است |
• | κ (واحد SI: m 2 ) نفوذپذیری محیط متخلخل است و |
• | Q m (واحد SI: kg/(m3 · s)) یک منبع جرم یا سینک است |
تأثیر گرانش و سایر نیروهای حجمی را می توان از طریق عبارت نیروی F (واحد SI: kg/(m 2 ·s 2 )) محاسبه کرد.
هنگامی که کادر اینرسی نادیده گرفته شده (جریان استوکس) انتخاب می شود، عبارت ( u · ∇)( u /ε p ) در سمت چپ معادله 7-52 غیرفعال می شود.
منبع انبوه، Qm ، حساب سپرده انبوه و ایجاد انبوه در دامنه ها است . تبادل جرم با سرعت صفر در نظر گرفته می شود.
گزینه های درگ Forchheimer و Ergun یک نیروی چسبناک متناسب با مجذور سرعت سیال اضافه می کنند، F = -ρβ| u | u ، در سمت راست معادله 7-52 ؛ برای جزئیات بیشتر به منابع رابط قانون دارسی مراجعه کنید .
در مورد جریان با چگالی متغیر، معادله 7-51 و معادله 7-52 باید همراه با معادله حالتی که چگالی را به دما و فشار مرتبط می کند حل شود (به عنوان مثال قانون گاز ایده آل).
برای جریان تراکم ناپذیر، چگالی در هر ذره سیال ثابت می ماند که می تواند به صورت بیان شود
و معادله تداوم ( معادله 7-51 ) به کاهش می یابد




