یک شرایط مرزی تابش موج صفحه ، تابش موج کروی ، یا تشعشع موج استوانهای را مشخص کنید تا به یک موج خروجی اجازه دهید با حداقل بازتاب از حوزه مدلسازی خارج شود. این شرایط را می توان با هندسه حوزه مدل سازی تطبیق داد. نوع موج هواپیما هم برای مرزهای میدان دور و هم برای پورت ها مناسب است (فقط برای امواج هواپیما). برای شرایط مرزی تشعشع عمومی برای موجبرها (پشتیبانی از حالت های چندگانه) توصیه می شود از شرایط مرزی پورت استفاده کنید.
شرایط مرزی تشعشع برای همه انواع مطالعات موجود است. برای مطالعه حوزه فرکانس، فرمول بندی مجدد Givoli و Neta از شرایط هیگدون ( مراجعه 1 ) برای امواج صفحه به مرتبه دوم اجرا شده است. برای امواج استوانه ای و کروی، COMSOL Multiphysics از عبارات مرتبه دوم مربوطه از Bayliss، Gunzburger و Turkel استفاده می کند ( مرجع 2 ). مطالعات گذرا، حالت، و فرکانس ویژه همان بسطها را به مرتبه اول اجرا میکنند.
شرایط مرزی تابش مرتبه اول در حوزه فرکانس خوانده می شود
که k عدد موج و κ ( r ) تابعی است که شکل آن به نوع موج بستگی دارد:
• | موج صفحه: κ ( r ) = 0 |
• | موج استوانه ای: κ ( r ) = 1 / ( 2 r ) |
• | موج کروی: κ ( r ) = 1 / r |
در حالت موج استوانه ای و کروی، r کوتاه ترین فاصله از نقطه r = ( x , y , z ) در مرز تا منبع است. سمت راست معادله یک میدان فشار ورودی اختیاری p i را نشان میدهد (به میدان فشار حادثه مراجعه کنید ).
شرایط مرزی تابش مرتبه دوم در حوزه فرکانس در زیر تعریف شده است. در این معادلات،  در یک نقطه معین از مرز، عملگر لاپلاس در صفحه مماس در آن نقطه خاص را نشان می دهد.
در یک نقطه معین از مرز، عملگر لاپلاس در صفحه مماس در آن نقطه خاص را نشان می دهد.
موج هواپیما
در نماد Givoli و Neta ( مراجعه 1 )، عبارات فوق با گزینه های پارامتر C 0 = C 1 = C 2 = ω / k مطابقت دارد . برای امواج معمولی فرود، این یک ضریب بازتاب ناپدید میدهد.
موج استوانه ای
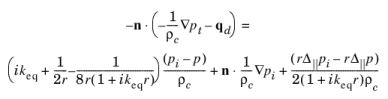
شرط مرزی موج استوانهای مبتنی بر گسترش سری موج خروجی در مختصات استوانهای است ( مراجعه 2 )، و فرض میکند که میدان مستقل از مختصات محوری است. محور این سیستم مختصات را با دادن جهت ( n x , n y , n z ) و یک نقطه ( x 0 , y 0 , z 0 ) روی محور مشخص کنید. در هندسه متقارن محوری، محور تقارن انتخاب طبیعی و تنها است.
موج کروی
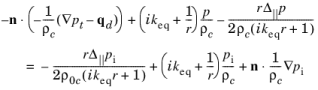
از یک موج کروی استفاده کنید تا به یک موج تابشی یا پراکنده – که از یک شی در مرکز نقطه ( x 0 , y 0 , z 0 ) که مشخص شده نشات می گیرد – اجازه دهید از حوزه مدل سازی بدون بازتاب خارج شود. شرط مرزی بر اساس یک بسط در مختصات کروی از Bayliss، Gunzburger، و Turkel ( مراجعه 2 )، اجرا شده به مرتبه دوم است.
تحلیل گذرا
شرط مرزی تابش گذرا عبارت مرتبه اول است
که در آن κ ( r ) همان تابع وابسته به نوع موج برای مورد فرکانس ویژه و p i میدان فشار تصادف اختیاری است .
تخمینی از ضریب انعکاس Rs برای امواج جعلی خارج از مرز تابش موج صفحه، برای امواج صفحه فرود در زاویه θ با عبارت زیر ارائه می شود: که در آن N ترتیب شرط مرزی است (اینجا 1 یا 2). بنابراین در فرود معمولی ( θ = 0) هیچ بازتاب کاذب وجود ندارد، در حالی که، برای مثال، در زاویه تابش 30 درجه برای N = 2 (تابش موج صفحه در حوزه فرکانس)، دامنه موج بازتابی کاذب 0.5٪ است. از حادثه |




