 |
میرایی ترموالاستیک در تشدید کننده MEMS
معرفی
تشدید کننده های MEMS با فاکتور با کیفیت بالا، اجزای کلیدی در صنعت نوظهور زمان بندی MEMS هستند. در این کاربردها یک تشدید کننده MEMS در فرکانس تشدید خود توسط یک حلقه فیدبک هدایت می شود تا مداری تولید کند که در فرکانس ثابت نوسان می کند. چنین ارجاعات فرکانسی در طیف وسیعی از دستگاه های الکترونیکی، از ساعت های CPU گرفته تا تلفن های همراه استفاده می شود. برای کاربردهای نوسانگر، فاکتور کیفیت تشدید کننده، همراه با پایداری فرکانس تشدید، عملکرد نهایی قابل دستیابی را تعیین می کند. تشدید کننده های فاکتور با کیفیت بالاتر در فرکانس رزونانس اوج بیشتری در طیف فرکانسی خود دارند و بنابراین فرکانس خاصی را با وفاداری بالاتر انتخاب می کنند. برای بسیاری از حالت های تشدید، حد فاکتور کیفیت قابل دستیابی با میرایی ترموالاستیک تعیین می شود.
برای درک میرایی ترموالاستیک، کشش یک میله الاستیک ایزوله حرارتی را در نظر بگیرید. هنگامی که چنین میله ای به طور یکنواخت و برگشت پذیر کشیده می شود دمای آن کاهش می یابد. کاهش دما افزایش آنتروپی ناشی از تنش در میله را جبران می کند (از آنجایی که فرآیند برگشت پذیر است، آنتروپی ثابت می ماند). به طور مشابه در فشرده سازی میله گرم می شود. هنگامی که یک سازه در حالت عادی پیچیده تر ارتعاش می کند، برخی از مناطق فشرده سازی و برخی از گسترش وجود دارد. بسته به مقیاس زمانی ارتعاش، گرما از قسمت های گرمتر سازه به قسمت های سردتر جریان می یابد. از آنجایی که جریان گرما یک فرآیند برگشت ناپذیر است، این جریان گرما با اتلاف انرژی از حالت ارتعاشی و میرایی متناظر برای حالت تشدید همراه است. میرایی ترموالاستیک به ویژه در سازه های MEMS کوچکتر مهم است.
تعریف مدل
مدل متشکل از یک پرتو تکی است که در حالت اصلی خود، عمود بر محور طولانی خود، ارتعاش می کند. هندسه مدل در شکل 1 نشان داده شده است . دو سر پرتو ثابت هستند و فرض می شود که به بدنه بسیار بزرگتری (به عنوان مثال، یک پد تماس) متصل هستند که به عنوان یک مخزن حرارتی عمل می کند.
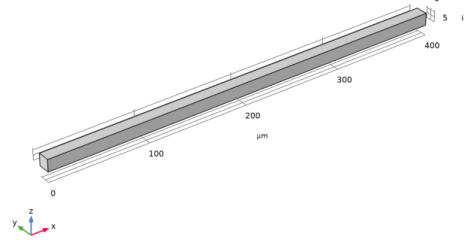
شکل 1: هندسه مدل متقارن. این هندسه از یک پرتو سیلیکونی به ضخامت 12 میکرومتر و طول 400 میکرومتر تشکیل شده است. عرض تیر 20 میکرومتر است اما از آنجایی که هندسه متقارن است فقط نیمی از عرض تیر نشان داده شده و از شرایط مرزی تقارن استفاده می شود. فرض بر این است که دو سر پرتو به بدنه ای با جرم حرارتی بزرگ، مانند یک پد تماس، متصل می شوند.
این تحلیل فاکتور کیفیت تشدید کننده را محاسبه می کند، با این فرض که میرایی ترموالاستیک مکانیسم میرایی غالب است. معادلات جفت شده ترموالاستیسیته در تشدید کننده حل می شوند.
استخراج معادلات ترموالاستیسیته
منابع 1 تا 7 اطلاعات پس زمینه مفیدی را ارائه می دهند.
معادلات ترموالاستیسیته از قانون اول ترمودینامیک به دست می آید که می توان آن را به صورت زیر بیان کرد:
(1)
که در آن dU تغییر انرژی داخلی است، dQ’ جریان گرما به سیستم است (در این مورد عدد اول نشان دهنده یک دیفرانسیل غیر دقیق است) و dW’ کار انجام شده روی سیستم است. برای بخش کوچکی از یک جامد (به اندازه کافی کوچک که تنش ها و کرنش ها یکنواخت هستند)، با چگالی مرجع اولیه ρ 0 ، قانون اول را می توان به شکل زیر بازنویسی کرد (با فرض اینکه تغییرات دیفرانسیل بین حالت های تعادل رخ می دهد):
(2)
که در آن T a دمای مطلق است، s آنتروپی در واحد جرم است، σ بخش الاستیک تنش دوم Piola-Kirchhoff (به طور کلی تانسور رتبه 2)، ε کرنش ماده (همچنین یک تانسور) است. به طور کلی تانسور تنش دوم Piola-Kirchhoff، p ، باید به بخش های الاستیک ( σ ) و غیر الاستیک ( τ ) تقسیم شود به طوری که:
بخش الاستیک تانسور تنش، σ ، کار می کند σ : d ε در طول تغییر در کرنش. بخش غیر کشسان تانسور کرنش، τ ، هنگام تغییر کرنش، گرما را با نرخ τ 🙁 d ε/ d τ ) تولید می‌کند و با میرایی داخلی یا ماده مشخص می‌شود. این مکانیسم های میرایی داخلی با پدیده های میکروسکوپی مانند حرکت دررفتگی همراه هستند.
از معادله 2 می توان شناسایی های زیر را برای Ta و σ انجام داد :
سپس معادله تعادل آنتروپی باید استخراج شود. از آنجا که ترموالاستیسیته شامل فرآیندهای برگشت ناپذیر است، فرض تعادل مورد نیاز برای استخراج معادله 2 دیگر معتبر نیست. در عوض، یک فرض تعادل «محلی» ساخته شده است. فرض بر این است که اگرچه سیستم در تعادل نیست، اما در عناصر کوچک حالتی از تعادل محلی وجود دارد که برای آن آنتروپی محلی در واحد جرم، s وجود دارد.، همان تابع انرژی داخلی، کرنش و عدد ذره است که در حالت تعادل بود. این فرض معمولاً در مدلسازی پدیده‌های حمل‌ونقل به کار می‌رود و تنها با اعتبار نتایج حاصل از آن و نتایج به‌دست‌آمده از مدل‌های میکروسکوپی خاص، برای موقعیت‌های نزدیک به تعادل توجیه می‌شود. برای یک عنصر حجم کوچک در قاب مواد، معادله 2 را می توان به صورت نوشتاری نوشت
سپس می توان نرخ تغییر آنتروپی را به صورت نوشتاری نوشت
(3)
از قانون اول ( معادله 1 ) میزان تغییر انرژی داخلی به صورت زیر بدست می آید:
که w کار انجام شده در واحد حجم و q گرمای انباشته شده در واحد حجم است. گرمای انباشته شده را می توان به صورت مجموع منابع گرما و واگرایی در شار حرارتی قاب مواد نوشت:
که در آن Q منبع گرما در واحد حجم و τ بخش غیر کشسان تانسور تنش است. سرعت انجام کار (در واحد حجم مرجع) توسط یک ماده الاستیک خطی توسط بخش الاستیک دومین تنش Piola-Kirchhoff منقبض شده با نرخ کرنش ماده به دست می‌آید. در واحد حجم معادله زیر به دست می آید:
بنابراین معادله 3 به کاهش می یابد
تعریف رسانایی حرارتی مواد را می دهد
که در آن κ رسانایی حرارتی است که در قاب ماده تعریف شده است.
بنابراین معادله است
(4)
اکنون لازم است عبارتی برای نرخ تغییر آنتروپی با توجه به زمان استخراج کنیم. برای انجام این کار یک بار دیگر از فرض تعادل محلی استفاده می شود. با استفاده از معادله 2 معادله نوشته می شود
که یک پتانسیل ترمودینامیکی جدید را تعریف می کند ، انرژی آزاد گیبس در واحد جرم، داده شده توسط
تغییرات انرژی آزاد گیبس در واحد جرم شکل می گیرد
که منجر به روابط می شود
با متمایز کردن هر یک از معادلات بالا برای بار دوم، می توان رابطه ماکسول زیر را استخراج کرد
(5)
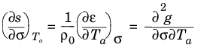
اکنون می توان یک عبارت برای آنتروپی جامد استخراج کرد. با فرض اینکه تنش الاستیک تابعی معکوس از کرنش است، می توانیم s = s ( σ , Ta ) بنویسیم. بدین ترتیب،
با استفاده از رابطه ماکسول در معادله 5 به دست می آید
به طوری که
طبق تعریف، ظرفیت گرمایی جامد در تنش ثابت با استفاده از
بدین ترتیب،
(6)
با جایگزینی معادله 6 به معادله 4 ، معادله زیر برای ترموالاستیسیته به دست می آید:
(7)
یک عبارت منبع گرمایی اضافی در معادله 7 در مقایسه با معادلات استاندارد انتقال حرارت در جامدات موجود است. این اصطلاح مشکل ساختاری را با مشکل انتقال حرارت جفت می کند. به نوبه خود، معادله انتقال حرارت از طریق رابطه سازنده به مشکل ساختاری بازگشت. نرم افزار COMSOL Multiphysics یک شکل خطی از معادلات ترموالاستیسیته ناهمسانگرد ارائه شده در معادله 7 را حل می کند .
در مورد خاصی از مواد الاستیک خطی (در صورت عدم وجود میرایی)، تنش و کرنش با قانون دوهامل هوک مرتبط است:
که در آن C تانسور الاستیسیته، σi تنش اولیه، εi کرنش اولیه و T ref دمای مرجعی است که در آن کرنش و تنش ها مقادیر اولیه را می گیرند .
این معادله معادله انتقال حرارت را با مسئله ساختاری جفت می کند. با توجه به انبساط حرارتی مستقل از دما، و عدم میرایی مواد، معادله 7 شکل می گیرد
که شکل معمول معادله ترموالاستیسیته خطی است.
نتایج و بحث
شکل 2 شکل حالت و توزیع دمای مربوطه را در پرتو نشان می دهد. این حالت دارای فرکانس ویژه 63.3 کیلوهرتز و ضریب کیفیت 10700 است . زنر یک بیان تحلیلی تقریبی را برای ضریب کیفیت یک پرتو نازک همسانگرد که در حالت اصلی خود ارتعاش می‌کند، تنها با در نظر گرفتن شیب‌های حرارتی در جهت خمش به دست آورد. بیان زنر توسط:
(8)
که در آن E مدول یانگ پرتو است، α انبساط حرارتی همسانگرد، ω فرکانس رزونانس زاویه‌ای مکانیکی و τ ثابت زمانی آرامش حرارتی سیستم است که به‌واسطه:
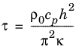
که در آن h ضخامت پرتو و κ رسانایی حرارتی مد است. فرکانس تشدید پرتو را می توان به صورت تحلیلی نیز محاسبه کرد و به وسیله:
(9)
جدول 1 مدل Multiphysics COMSOL را با مقادیر محاسبه شده با استفاده از معادله 8 و معادله 9 و با نتایج تجربی به دست آمده از Ref. 7 . توجه داشته باشید که مدل COMSOL Multiphysics ضریب کیفیت کمی بالاتر از نتیجه نظری دارد زیرا برخی از گرادیان های حرارتی با شرایط مرزی همدما حذف می شوند (اگر یک شرط مرزی عایق حرارتی به مرزهای انتهایی اعمال شود ضریب کیفیت به طور قابل توجهی کاهش می یابد – در تمرین شرط مرزی واقعی جایی بین این دو حد است).
شکل 2: شکل حالت اساسی و توزیع دمای متناظر درون پرتو.
منبع | فرکانس تشدید (MHZ) | فاکتور کیفیت |
مدل COMSOL | 0.63 | 11. 2× 10 3 |
معادله 8 و معادله 9 | 0.63 | 10.3 × 10 3 |
آزمایش ( مراجعه 7 ) | 0.57 | 10.3 × 10 3 |
منابع
1. سی جی ادکینز، ترمودینامیک تعادل ، انتشارات دانشگاه کمبریج، 1983.
2. W. Yourgrau, A. van der Merwe, and G. Raw, Treatise on Reversible and Statistical Thermodynamics: An Introduction to Noclassical Thermodynamics , Dover Publications, Inc., New York, 2002.
3. سی. زنر، “اصطکاک داخلی در جامدات I: نظریه اصطکاک داخلی در نی”، بررسی فیزیکی ، جلد. 52، ص 90-99، 1937.
4. سی. زنر، “اصطکاک داخلی در جامدات II: نظریه عمومی اصطکاک داخلی ترموالاستیک”، بررسی فیزیکی ، جلد. 53، ص 230-235، 1938.
5. ME Gurtin، E. Fied، و L. Anand، مکانیک و ترمودینامیک Continua ، انتشارات دانشگاه کمبریج، 2010.
6. VA Lubarda، “در مورد پتانسیل های ترمودینامیکی در ترموالاستیسیته خطی”، بین المللی. J. Solids and Structures , vol. 41، شماره 26، صفحات 7377-7398، 2004.
7. آ . دوول، آر. 15، نه 6، صص 1437-1445، 2006.
مسیر کتابخانه برنامه: MEMS_Module/ Actuators/thermoelastic_damping_3d
دستورالعمل مدلسازی
از منوی File ، New را انتخاب کنید .
جدید
در پنجره جدید ، روی 
Model Wizard کلیک کنید .
Model Wizard کلیک کنید .مدل جادوگر
1 | در پنجره Model Wizard ، روی  3D کلیک کنید . |
2 | در درخت Select Physics ، Structural Mechanics>Thermal-Structure Interaction>Thermoelasticity را انتخاب کنید . |
3 | روی افزودن کلیک کنید . |
4 |  روی مطالعه کلیک کنید . |
5 | در درخت مطالعه انتخاب ، مطالعات از پیش تعیین شده برای واسط های فیزیک انتخاب شده > انتقال حرارت در جامدات> آشفتگی حرارتی، فرکانس ویژه را انتخاب کنید . |
6 |  روی Done کلیک کنید . |
هندسه 1
Model Wizard به گره Geometry در ساختار درختی Model Builder منتهی شد. ساخت سازه تیر ساده را با تعیین یک واحد طول مناسب شروع کنید.
1 | در پنجره Model Builder ، در قسمت Component 1 (comp1) روی Geometry 1 کلیک کنید . |
2 | در پنجره تنظیمات هندسه ، بخش Units را پیدا کنید . |
3 | از لیست واحد طول ، میکرومتر را انتخاب کنید . |
بلوک 1 (blk1)
1 | در نوار ابزار Geometry ، روی  Block کلیک کنید . |
2 | در پنجره تنظیمات برای Block ، قسمت Size and Shape را پیدا کنید . |
3 | در قسمت متن Width عدد 400 را تایپ کنید . |
4 | در قسمت Depth text عدد 12 را تایپ کنید . |
5 | در قسمت متن ارتفاع ، 12 را تایپ کنید . |
6 |  روی Build All Objects کلیک کنید . |
پارامترهای مواد را از یک فایل وارد کنید.
تعاریف جهانی
پارامترهای 1
1 | در پنجره Model Builder ، در قسمت Global Definitions روی Parameters 1 کلیک کنید . |
2 | در پنجره تنظیمات برای پارامترها ، بخش پارامترها را پیدا کنید . |
3 |  روی Load from File کلیک کنید . |
4 | به پوشه Application Libraries مدل بروید و روی فایل thermoelastic_damping_3d_parameters.txt دوبار کلیک کنید . |
یک متریال خالی ایجاد کنید و با استفاده از پارامترهایی که به تازگی وارد کردیم، ویژگی های مواد را پر کنید.
مواد
مواد 1 (mat1)
1 | در پنجره Model Builder ، در قسمت Component 1 (comp1) روی Materials راست کلیک کرده و Blank Material را انتخاب کنید . |
2 | در پنجره تنظیمات برای Material ، قسمت Material Contents را پیدا کنید . |
3 | در جدول تنظیمات زیر را وارد کنید: |
ویژگی | متغیر | ارزش | واحد | گروه اموال |
مدول یانگ | E | E0 | پا | مدول یانگ و نسبت پواسون |
نسبت پواسون | نه | اکنون 0 | 1 | مدول یانگ و نسبت پواسون |
تراکم | rho | put0 | کیلوگرم بر متر مکعب | پایه ای |
رسانایی گرمایی | k_iso ; kii = k_iso، kij = 0 | kappa0 | W/(m·K) | پایه ای |
ظرفیت گرمایی در فشار ثابت | Cp | Cp0 | J/(kg·K) | پایه ای |
ضریب انبساط حرارتی | alpha_iso ; alphaii = alpha_iso، alphaij = 0 | آلفا0 | 1/K | پایه ای |
شرایط مرزی را تنظیم کنید برای قسمت مکانیک جامدات، تیر در دو سر ثابت است و در یکی از اضلاع آن دارای تقارن BC است.
مکانیک جامدات (جامدات)
محدودیت ثابت 1
1 | در پنجره Model Builder ، در قسمت Component 1 (comp1) روی Solid Mechanics (solid) کلیک راست کرده و Fixed Constraint را انتخاب کنید . |
2 | فقط مرزهای 1 و 6 را انتخاب کنید. |
تقارن 1
1 | در نوار ابزار Physics ، روی  Boundaries کلیک کنید و Symmetry را انتخاب کنید . |
2 | فقط مرز 2 را انتخاب کنید. |
برای قسمت انتقال حرارت، دمای دو سر پرتو در دمای ثابت پیش فرض ثابت می شود. برای مرحله مطالعه فرکانس ویژه ، همان شرایط مرزی دما ، انحراف دما را روی صفر تنظیم می کند.
انتقال حرارت در جامدات (HT)
در پنجره Model Builder ، در قسمت Component 1 (comp1) روی انتقال حرارت در جامدات (ht) کلیک کنید .
دما 1
1 | در نوار ابزار Physics ، روی  Boundaries کلیک کنید و Temperature را انتخاب کنید . |
2 | فقط مرزهای 1 و 6 را انتخاب کنید. |
یک مش ساختار یافته برای پرتو ایجاد کنید.
مش 1
نقشه برداری 1
1 | در نوار ابزار Mesh ، روی  Boundary کلیک کنید و Mapped را انتخاب کنید . |
2 | فقط مرز 1 را انتخاب کنید. |
توزیع 1
1 | روی Mapped 1 کلیک راست کرده و Distribution را انتخاب کنید . |
2 | فقط لبه های 1 و 2 را انتخاب کنید. |
جارو 1
در نوار ابزار Mesh ، روی Swept کلیک کنید .
Swept کلیک کنید .توزیع 1
1 | روی Swept 1 کلیک راست کرده و Distribution را انتخاب کنید . |
2 | در پنجره تنظیمات برای توزیع ، بخش توزیع را پیدا کنید . |
3 | در قسمت متنی Number of Elements عدد 70 را تایپ کنید . |
4 |  روی ساخت همه کلیک کنید . |
به مطالعه فرکانس ویژه حدس اولیه خوبی بدهید. از گزینه Larger real part برای جلوگیری از حالت های جعلی نزدیک به فرکانس صفر استفاده کنید .
مطالعه 1
مرحله 2: فرکانس ویژه
1 | در پنجره Model Builder ، در مطالعه 1 ، روی مرحله 2: فرکانس ویژه کلیک کنید . |
2 | در پنجره تنظیمات برای Eigenfrequency ، قسمت Study Settings را پیدا کنید . |
3 | کادر بررسی تعداد دلخواه فرکانس ویژه را انتخاب کنید . در فیلد متن مرتبط، 1 را تایپ کنید . |
4 | تیک Search for eigenfrequencies around را انتخاب کنید . در قسمت متن مرتبط، 0.63e6 را تایپ کنید . |
5 | از روش جستجوی فرکانس ویژه در اطراف لیست شیفت ، قسمت واقعی بزرگتر را انتخاب کنید . |
از آنجایی که مرحله مطالعه ثابت فقط برای محاسبه نقطه خطی سازی برای مطالعه مقدار ویژه (مرتبط با جابجایی صفر و دمای یکنواخت) استفاده می شود، متغیرهای وابسته باید به صورت دستی مقیاس شوند.
راه حل 1 (sol1)
1 | در نوار ابزار مطالعه ، روی  Show Default Solver کلیک کنید . |
2 | در پنجره Model Builder ، گره Solution 1 (sol1) را گسترش دهید ، سپس روی Dependent Variables 1 کلیک کنید . |
3 | در پنجره تنظیمات برای متغیرهای وابسته ، بخش Scaling را پیدا کنید . |
4 | از لیست روش ، دستی را انتخاب کنید . |
5 | در نوار ابزار مطالعه ،  روی محاسبه کلیک کنید . |
نتایج
شکل حالت (جامد)
تغییر شکل شکل حالت را به نمودار دمای پیش فرض اضافه کنید.
دما (ht)
1 | در پنجره Model Builder ، روی دما (ht) کلیک کنید . |
2 | در پنجره Settings for 3D Plot Group ، بخش Color Legend را پیدا کنید . |
3 | تیک Show legends را پاک کنید . |
تغییر شکل 1
1 | در پنجره Model Builder ، گره Temperature (ht) را گسترش دهید . |
2 | روی Surface کلیک راست کرده و Deformation را انتخاب کنید . |
3 | در نوار ابزار دما (ht) ، روی  Plot کلیک کنید . |
نمودار را با شکل 2 مقایسه کنید .
خطوط همدما (ht)
1 | در پنجره Model Builder ، در بخش Results روی خطوط همدما (ht) کلیک کنید . |
2 | در پنجره Settings for 3D Plot Group ، بخش Color Legend را پیدا کنید . |
3 | تیک Show legends را پاک کنید . |
ضریب Q را محاسبه کنید.
ارزیابی جهانی 1
1 | در نوار ابزار نتایج ، روی ارزیابی  جهانی کلیک کنید . |
2 | در پنجره تنظیمات برای ارزیابی جهانی ، روی جایگزینی عبارت در گوشه سمت راست بالای بخش عبارات کلیک کنید . از منو، Component 1 (comp1)>Solid Mechanics>Global>solid.Q_eig – ضریب کیفیت برای مقدار ویژه را انتخاب کنید . |
3 |  روی ارزیابی کلیک کنید . |
نتیجه را با نتایج جدول 1 مقایسه کنید .
