معرفی
معادله Korteweg-de Vries (KdV) که در سال 1895 توسط Korteweg و de Vries فرموله شد، امواج آب را مدلسازی می کند. این به شدت با معادله برگرز در تضاد است زیرا هیچ اتلاف ایجاد نمی کند و امواج به ظاهر برای همیشه حرکت می کنند. در سال 1965، Zabusky و Kruskal چنین امواجی را سالیتون نامیدند .
معادله KdV با شرایط مرزی و مقدار اولیه به صورت فرموله شده است
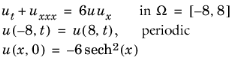
این معادله شیببندی و پراکندگی جبهههای موج را مدلسازی میکند، اما قطاری از امواج هارمونیک ساده را پشتیبانی نمیکند. چنین قطارهایی شامل تاج های موجی هستند که معمولاً با اقیانوس مرتبط هستند: صرفاً یک تداخل سازنده لحظه ای امواج کمک کننده که با سرعت های مختلف حرکت می کنند. با این حال، این معادله از سالیتونها پشتیبانی میکند، “کوهان” منفرد که بدون تغییر شکل یا سرعت برای مسافتهای غیرمنتظره طولانی حرکت میکنند.
در واقع، پری و شیمکه ( مراجعه 2 ) از اندازه گیری های اقیانوس شناسی کشتی به این نتیجه رسیدند که نوارهای آب متلاطم در دریای آندامان، که در شرق خلیج بنگال و غرب برمه (اتحادیه میانمار) و تایلند قرار دارد، با دامنه امواج داخلی اقیانوسی تصاویر ماهواره ای از آن زمان مشخص کرده است که این امواج از کرانه های کم عمق روی لایه ای بین آب گرم و سرد منشاء می گیرند. علاوه بر این، آزبورن و برچ ( مراجعه 1 ) داده های اقیانوس شناسی را در تلاشی برای ارزیابی نیروهای نوسانات جریان زیرآبی مرتبط با چنین امواجی در دکل های حفاری دریایی تجزیه و تحلیل کردند. آنها به این نتیجه رسیدند که نوارهای زبری مشاهده شده بصری توسط سالیتون های داخلی ایجاد می شوند که از معادله KdV پیروی می کنند ( مراجعه 3 ).
توسعه جدیدتر، استفاده از معادله KdV برای نوع دیگری از امواج – امواج نور است. امروزه سالیتون ها کاربرد عملی اولیه خود را در فیبرهای نوری دارند. به طور خاص، خواص پراکندگی خطی یک فیبر یک موج را یکسان می کند در حالی که خواص غیرخطی یک اثر تمرکز می دهد. نتیجه یک نبض بسیار پایدار و با عمر طولانی است ( مرجع 3 ). شگفت انگیز است که محققان فرمولی برای چنین امواجی کشف کرده اند:
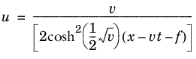
این معادله می گوید که سرعت پالس چیزی است که دامنه پالس و عرض پالس را تعیین می کند. شبیه سازی زیر این اثر را نشان می دهد. یک پالس اولیه، که با فرمول مطابقت ندارد، بلافاصله به دو پالس با دامنه ها و سرعت های مختلف تجزیه می شود. دو پالس جدید از فرمول پیروی می کنند و بنابراین می توانند برای همیشه حرکت کنند. در حالی که فرمول نحوه برهمکنش سالیتونها را نشان نمیدهد، شبیهسازی نشان میدهد که آنها میتوانند با هم برخورد کرده و ظاهراً بدون تغییر ظاهر شوند، درست مانند امواج خطی، مشاهدات غیر شهودی دیگری که مشاهده آن بدون پیشبینی توسط محاسبات دشوار است.
تعریف مدل
در مدل، اصطلاح uu x تمرکز یک موج را توصیف می کند و u xxx به پراکندگی آن اشاره دارد. تعادل این دو عبارت به امواج اجازه می دهد تا با شکل بدون تغییر حرکت کنند.
از آنجا که COMSOL Multiphysics مشتقات سوم را مستقیماً ارزیابی نمی کند، معادله اصلی بالا را به عنوان یک سیستم از دو متغیر بازنویسی می کنید تا آن را حل کنید:
با استفاده از رابط PDE فرم عمومی، باید دو متغیر وابسته u1 و u2 را تعریف کنید و ضرایب d a ، Γ و F را در معادله زیر مشخص کنید:
• | فقط معادله اول مشتق زمانی دارد و آن نسبت به u 1 است ، بنابراین فقط d a (1,1) 1 است . سه جزء دیگر صفر هستند. |
• | واگرایی یک مشتق فضایی با توجه به x است . این بدان معنی است که مولفه Γ از معادله اول u 2 است که شما آن را به صورت u2 تایپ می کنید . مولفه Γ از معادله دوم u 1 x است که با استفاده از نحو COMSOL Multiphysics به صورت u1x بیان می کنید . |
• | مولفه های ترم F سمت راست معادلات هستند: F 1 6 u 1 u 1 x ( نوع 6*u1*u1x ) و F 2 u 2 است (نوع u2 ). |
شرط اولیه برای u 1 از تابع کسینوس هذلولی برای ارائه یک شکل موج جالب برای شروع استفاده می کند. برای u 2 ، شما باید دومین مشتق فضایی این تابع را ارائه دهید تا شرایط اولیه منسجم را فراهم کند.
شرایط مرزی شرایط مرزی دوره ای هستند: راه حل در یک سر همیشه با جوابی که در انتهای دیگر دامنه قرار دارد یکسان است.
نتایج
نمودار زیر نشان می دهد که چگونه سالیتون ها با هم برخورد می کنند و دوباره ظاهر می شوند و شکلشان دست نخورده است.
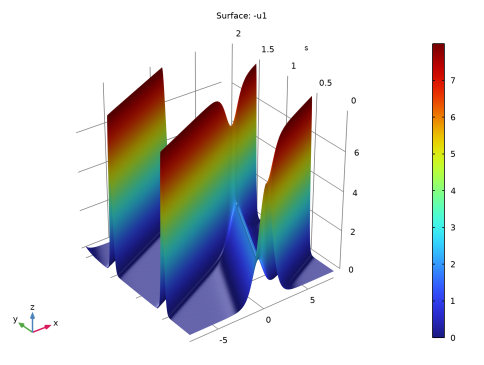
شکل 1: راه حلی که برخورد سالیتون را تجسم می کند.
منابع
1. AR Osborne و TL Burch, “Internal Solitons in the Andaman Sea”, Science , vol. 208، شماره 4443، صفحات 451-460، 1980.
2. RB Perry و GR Schimke، “موجهای داخلی با دامنه بزرگ مشاهده شده در ساحل شمال غربی سوماترا”، J. Geophys. Res. ، جلد 70، شماره 10، صص 2319-2324، 1965.
3. جی. استرنگ، ریاضیات کاربردی ، ولزلی-کمبریج، 1986.
مسیر کتابخانه برنامه: COMSOL_Multiphysics/Equation_Based/kdv_equation
دستورالعمل مدلسازی
از منوی File ، New را انتخاب کنید .
جدید
در پنجره جدید ، روی  Model Wizard کلیک کنید .
Model Wizard کلیک کنید .
مدل جادوگر
1 | در پنجره Model Wizard ، روی |
2 | در درخت انتخاب فیزیک ، ریاضیات> رابط های PDE> فرم عمومی PDE (g) را انتخاب کنید . |
3 | روی افزودن کلیک کنید . |
4 | در قسمت متنی Number of varpendable variables ، 2 را تایپ کنید . |
5 |
6 | در درخت انتخاب مطالعه ، General Studies>Time Dependent را انتخاب کنید . |
7 |
ریشه
1 | در پنجره Model Builder ، روی گره ریشه کلیک کنید. |
2 | در پنجره تنظیمات گره ریشه ، بخش Unit System را پیدا کنید . |
3 | از لیست سیستم واحد ، هیچکدام را انتخاب کنید . |
پیگیری واحدها در این مدل مهم نیست. با خاموش کردن پشتیبانی واحد، از نیاز به تعیین ابعاد برای ضرایب معادله و مختصات برای خلاص شدن از شر هشدارهای واحد جلوگیری می کنید.
هندسه 1
فاصله 1 (i1)
1 | در پنجره Model Builder ، در قسمت Component 1 (comp1) روی Geometry 1 کلیک راست کرده و Interval را انتخاب کنید . |
2 | در پنجره تنظیمات برای فاصله ، قسمت فاصله را بیابید . |
3 | در جدول تنظیمات زیر را وارد کنید: |
مختصات |
-8 |
8 |
فرم عمومی PDE (G)
شرایط دوره ای 1
1 | در پنجره Model Builder ، در قسمت Component 1 (comp1) روی General Form PDE (g) کلیک راست کرده و Periodic Condition را انتخاب کنید . |
2 | در پنجره تنظیمات برای شرایط دوره ای ، قسمت انتخاب مرز را پیدا کنید . |
3 | از لیست انتخاب ، همه مرزها را انتخاب کنید . |
فرم عمومی PDE 1
1 | در پنجره Model Builder ، روی General Form PDE 1 کلیک کنید . |
2 | در پنجره تنظیمات برای فرم عمومی PDE ، بخش Conservative Flux را پیدا کنید . |
3 | در آرایه فیلد متنی Γ ، u2 را در ردیف اول تایپ کنید. |
4 | در آرایه فیلد متنی Γ ، u1x را در ردیف دوم تایپ کنید. |
5 | قسمت Source Term را پیدا کنید . در آرایه فیلد متنی f ، 6*u1*u1x را در ردیف اول تایپ کنید. |
6 | در آرایه فیلد متنی f ، u2 را در ردیف دوم تایپ کنید. |
7 | قسمت Damping یا Mass Coefficient را پیدا کنید . در آرایه d a text-field، 0 را در ستون دوم ردیف دوم تایپ کنید. |
مقادیر اولیه 1
1 | در پنجره Model Builder ، روی مقادیر اولیه 1 کلیک کنید . |
2 | در پنجره تنظیمات برای مقادیر اولیه ، قسمت مقادیر اولیه را پیدا کنید . |
3 | در قسمت متنی u 1 ، -6*sech(x)^2 را تایپ کنید . |
4 | در قسمت نوشتاری u 2 ، -24*sech(x)^2*tanh(x)^2+12*sech(x)^2*(1-tanh(x)^2) را تایپ کنید . |
مش 1
لبه 1
در نوار ابزار Mesh ، روی  Edge کلیک کنید .
Edge کلیک کنید .
اندازه
1 | در پنجره Model Builder ، روی Size کلیک کنید . |
2 | در پنجره تنظیمات برای اندازه ، قسمت اندازه عنصر را پیدا کنید . |
3 | روی دکمه Custom کلیک کنید . |
4 | قسمت پارامترهای اندازه عنصر را پیدا کنید . در قسمت متن حداکثر اندازه عنصر ، 0.1 را تایپ کنید . |
5 |
مطالعه 1
مرحله 1: وابسته به زمان
1 | در پنجره Model Builder ، در بخش مطالعه 1 ، روی Step 1: Time Dependent کلیک کنید . |
2 | در پنجره تنظیمات مربوط به زمان وابسته ، قسمت تنظیمات مطالعه را پیدا کنید . |
3 | در قسمت متنی زمان خروجی ، range(0,0.0025,2) را تایپ کنید . |
4 | از لیست Tolerance ، User controlled را انتخاب کنید . |
5 | در قسمت متنی Relative tolerance ، 3e-6 را تایپ کنید . |
راه حل 1 (sol1)
1 | در نوار ابزار مطالعه ، روی |
2 | در پنجره Model Builder ، گره Solution 1 (sol1) را گسترش دهید ، سپس روی Time-Dependent Solver 1 کلیک کنید . |
3 | در پنجره تنظیمات برای حل وابسته به زمان ، برای گسترش بخش Time Steping کلیک کنید . |
4 | از لیست روش ، آلفای تعمیم یافته را انتخاب کنید . |
استپر زمان آلفای تعمیم یافته برای مسائل موجی مناسب است. برای یک راه حل دقیق، از تنظیمات تحمل سخت تر استفاده کنید.
5 | برای گسترش بخش Absolute Tolerance کلیک کنید . از لیست روش تحمل ، دستی را انتخاب کنید . |
6 | در قسمت متنی Absolute tolerance ، 3e-7 را تایپ کنید . |
7 | قسمت Time Steping را پیدا کنید . در قسمت متنی تقویت برای فرکانس بالا ، 0.98 را تایپ کنید . |
8 | در پنجره Model Builder ، گره Study 1>Solver Configurations>Solution 1 (sol1)>Time-Dependent Solver 1 را گسترش دهید ، سپس روی Fully Coupled 1 کلیک کنید . |
9 | در پنجره Settings for Fully Coupled ، برای گسترش بخش Method and Termination کلیک کنید . |
10 | در قسمت متنی Tolerance factor 0.1 را تایپ کنید . |
11 | در نوار ابزار مطالعه ، |
نتایج
گروه طرح 1 بعدی 1
1 | در پنجره Settings for 1D Plot Group ، بخش Data را پیدا کنید . |
2 | از لیست انتخاب زمان ، از لیست را انتخاب کنید . |
3 | در لیست Times (s) 0.025 را انتخاب کنید . |
نمودار خطی 1
1 | در پنجره Model Builder ، گره 1D Plot Group 1 را گسترش دهید ، سپس روی Line Graph 1 کلیک کنید . |
2 | در پنجره تنظیمات برای نمودار خط ، بخش y-Axis Data را پیدا کنید . |
3 | در قسمت Expression text -u1 را تایپ کنید . |
4 | در نوار ابزار 1D Plot Group 1 ، روی 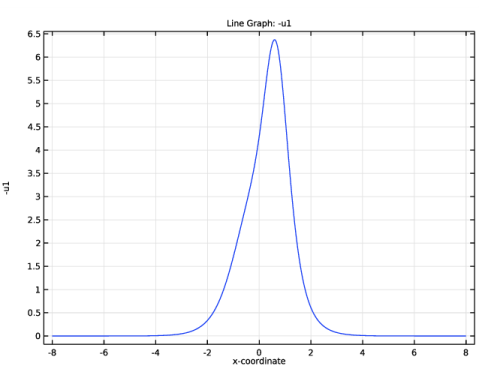 |
حل معادله KdV در 0.025 ثانیه.
برای تجسم محلول، نتایج را در امتداد محور زمان اکسترود کنید.
اکستروژن پارامتریک 1D 1
در نوار ابزار Results ، روی  More Datasets کلیک کنید و Parametric Extrusion 1D را انتخاب کنید .
More Datasets کلیک کنید و Parametric Extrusion 1D را انتخاب کنید .
گروه دو بعدی پلات 2
در نوار ابزار نتایج ، روی  2D Plot Group کلیک کنید .
2D Plot Group کلیک کنید .
سطح 1
1 | روی 2D Plot Group 2 کلیک راست کرده و Surface را انتخاب کنید . |
2 | در پنجره تنظیمات برای Surface ، بخش Expression را پیدا کنید . |
3 | در قسمت Expression text -u1 را تایپ کنید . |
بیان قد 1
1 | روی Surface 1 کلیک راست کرده و Height Expression را انتخاب کنید . |
2 |
با نمودار نشان داده شده در شکل 1 مقایسه کنید .




