معادله تداوم به دست آمده برای یک حجم کنترل به دست آمده است
(9-1)
و معادله موازنه تکانه مربوطه می باشد
(9-2)
که در آن Z محیط داخلی لوله است و A = A ( x , p , … ) سطح مقطع خیس شده داخلی است، u میانگین سرعت متوسط منطقه است که در جهت مماسی u = تعریف می شود. u e t ، p میانگین فشار در طول لوله، τ w نیروی کشش دیوار و F نیروی حجمی است. گرادیان در جهت مماسی e t گرفته شده است . اصطلاح βیک ضریب تصحیح پروفیل جریان است که میانگین مجذور سرعت کل را به مجذور سرعت میانگین مرتبط می کند. به طوری که
(9-3)
جایی که
پارامترهای محلی غیر میانگین هستند. باز هم p و u متغیرهای وابسته میانگین مساحت هستند.
خطی سازی
معادلات حاکم اکنون خطی شده اند. یعنی همه متغیرها با فرض مقادیر مرتبه صفر ثابت (ویژگی های پس زمینه حالت پایدار) به مرتبه اول گسترش می یابند. تغییرات صوتی متغیرهای وابسته کوچک و بالای مقادیر پسزمینه فرض میشوند. این کار بر اساس طرح زیر انجام می شود:
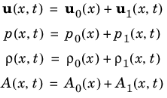
که در آن A 0 اغلب فقط تابع x است . با این حال، A 0 را می توان توسط عوامل خارجی مانند حرارت یا تغییر شکل ساختاری، بنابراین وابستگی زمانی تغییر داد. اصطلاحات مرتبه اول آشفتگی های کوچکی را در بالای مقادیر پس زمینه نشان می دهند (ترتیب صفر). آنها معتبر هستند
علاوه بر این، اغتشاشات برای چگالی سیال و سطح مقطع به مرتبه اول در p 0 در یک سری تیلور گسترش مییابد به طوری که
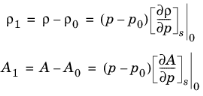
جایی که زیرنویس s به آنتروپی ثابت اشاره دارد. یعنی فرآیندها ایزنتروپیک هستند. روابط برای تراکم پذیری سیال و تراکم پذیری سطح مقطع هستند
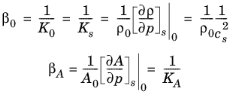
در اینجا β 0 تراکم پذیری سیال در فشار مرجع داده شده p 0 است ، سرعت توده ای همتروپیک صوت با cs نشان داده می شود و ρ 0 چگالی سیال در دمای مرجع و فشار مرجع داده شده است. β A تراکم پذیری موثر مقطع A 0 لوله به دلیل تغییرات در فشار سیال داخلی است. مدول توده ای K برابر با یک بر تراکم پذیری است.
قرار دادن بسط های فوق در معادلات حاکم ( معادله 9-1 و معادله 9-2 ) و حفظ فقط عبارت های مرتبه اول معادلات آکوستیک لوله از جمله جریان پس زمینه را به دست می دهد. اینها هستند:
(9-4)
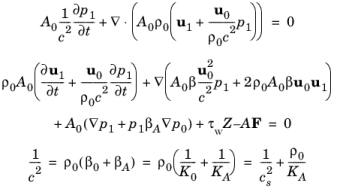
که در آن c سرعت موثر صوت در لوله است (شامل اثر ناشی از خواص کشسانی لوله که از طریق K A تعریف شده است ). مدول حجمی برای سطح مقطع K A با خواص مواد لوله مطابق با فرمول Korteweg به دست میآید (رجوع کنید به شماره 2 ). برای یک سیستم با دیواره های لوله سفت و سخت cs = c به عنوان K A به بی نهایت تمایل دارد.
با استفاده از این واقعیت که سرعت در امتداد جهت مماس e t گرفته می شود ، معادلات حاکم بر حسب مقادیر اسکالر u و p بازنویسی شده و بر روی مماس پیش بینی می شوند. زیرنویس 0 بر روی چگالی و مساحت و زیرنویس 1 نیز بر روی متغیرهای وابسته حذف می شود.
(9-5)
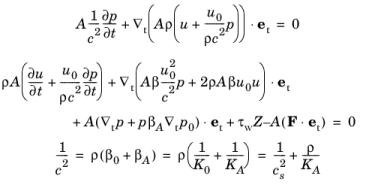
که در  آن مشتق مماسی است، τw نیروی کشش مماسی دیوار است (واحد SI: N/m2 ) و F یک نیروی حجمی است (واحد SI: N/ m3 ) .
آن مشتق مماسی است، τw نیروی کشش مماسی دیوار است (واحد SI: N/m2 ) و F یک نیروی حجمی است (واحد SI: N/ m3 ) .
معادلات حاکم
آکوستیک لوله، رابط گذرا
در نهایت، عبارت برای مشتق زمانی فشار در معادله تکانه با مشتقات فضایی با استفاده از معادله پیوستگی جایگزین میشود. این معادلات حل شده در Pipe Acoustics، رابط گذرا را به دست می دهد:
(9-6)
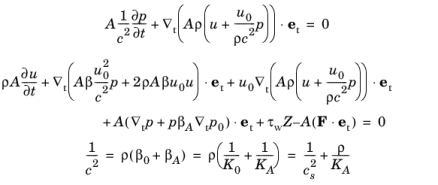
آکوستیک لوله، رابط دامنه فرکانس
در حوزه فرکانس همه متغیرها هارمونیک زمانی فرض می شوند به طوری که
(9-7)
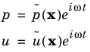
با وارد کردن این در معادله حاکم 9-6 (و رها کردن تایلد) معادلات حل شده در واسط Pipe Acoustics، Frequency Domain به دست می آید:
(9-8)
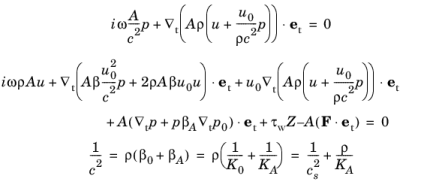
که در آن ω = 2 π f فرکانس زاویه ای و f فرکانس است.




