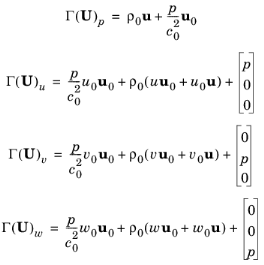معادلات حاکم حل شده در رابط معادله موج همرفت (CWE) انتشار امواج صوتی خطی (با فرض یک معادله حالت آدیاباتیک) در حضور یک جریان پسزمینه را توصیف میکنند. این معادله توسط Pierce در Ref. 1 (بخش 8.6) و رفر. 2 و معادلات حل شده توسط این رابط هستند،
(7-2)
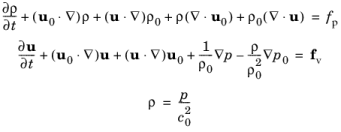
پیرس برای استفاده از فرض آدیاباتیک برای فرآیندهای آکوستیک (اختلال در آنتروپی، s = 0) و همچنین برای عدم حفظ متغیر آنتروپی مرتبه 0 s 0 (آنتروپی میانگین جریان پسزمینه) استدلال میکند. بحث این است که آنتروپی s فقط به دلیل تغییرات در زمینه های پس زمینه متفاوت است (در یک محیط همگن صفر است). این منجر به یک عبارت در معادله تکانه می شود که برای مثال در گرادیان های میدان پس زمینه مرتبه دوم است  و غیره. این شرایط نادیده گرفته می شود. این همچنین به این معنی است که معادلات زمانی معتبر نیستند که این عبارتها بزرگ باشند، به این معنی که گرادیانها در زمینههای پسزمینه بزرگ هستند.
و غیره. این شرایط نادیده گرفته می شود. این همچنین به این معنی است که معادلات زمانی معتبر نیستند که این عبارتها بزرگ باشند، به این معنی که گرادیانها در زمینههای پسزمینه بزرگ هستند.
به منظور تناسب با فرمول گالرکین ناپیوسته (dG)، معادلات حاکم باید در یک فرم محافظه کارانه کلی از نوع قرار گیرند.
(7-3)
که در آن U بردار حاوی متغیرهای وابسته ( p ، u )، d a ماتریس جرم سیستم، Γ ماتریس شار، و S بردار منبع سمت راست (RHS) است. شکل محافظه کارانه معادله 7-2 به شرح زیر است. با معادلات اویلر در یک فرم محافظه کارانه (با حذف RHS) شروع کنید. در حال حاضر، متغیرهای وابسته نشان دهنده میدان های کامل هستند (نه آشفتگی های صوتی). پیوستگی، تکانه و معادله حالت را می توان نوشت
(7-4)
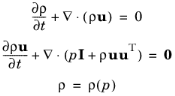
معادلات بقای جرم ρ و شار تکانه ρ u را توصیف می کنند . این معادلات را با استفاده از طرح معمول خطی کنید
اکنون، اینها را در معادله 7-4 وارد کنید و فقط عبارت های مرتبه اول (آشفتگی های صوتی) را حفظ کنید.
(7-5)
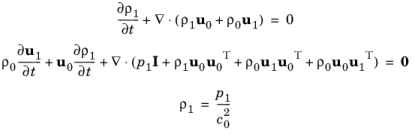
این شکل محافظه کارانه معادلات پیاده سازی شده در رابط CWE است. در باقیمانده این بخش، زیرنویس 1 از قسمت های آکوستیک حذف می شود. زیرنویس 0 روی متغیرهایی که خصوصیات میانگین پس زمینه را نشان می دهند نگه داشته می شود.
اکنون می توان معادله 7-5 را به شکلی که در معادله 7-3 ارائه شده است قرار داد و اجزای زیر را به دست آورد.
(7-6)

با u = [ u, v, w ] T و u 0 = [ u 0 , v 0 , w 0 ] T و اجزای شار عبارتند از
(7-7)