در بخش های زیر، مدل های ترمودینامیکی موجود توضیح داده شده است:
• | معادله مدل های حالت |
• | مدل های فاز مایع |
معادله مدل های حالت
مدل معادله حالت (EOS) یک رابطه جبری بین فشار مطلق ( P )، حجم مولی ( V ) و دمای مطلق ( T ) است. معادله ای از حالت که حداقل در حجم و به شکل مکعب باشد
(10-8)
که در آن Z ضریب تراکم پذیری و R ثابت گاز جهانی است، می تواند برای توصیف گازها و مایعات استفاده شود. معادلات حالت مکعبی به طور گسترده ای برای توصیف رفتار حجمی گاز و مایع سیالات خالص و همچنین تمام خواص دیگر با گسترش مخلوط ها استفاده می شود. مقایسه جامع مدل های مختلف EOS مکعبی را می توان در Ref. 2 و ر. 3 .
معادلات مدل های حالت موجود در پایگاه داده خواص ترمودینامیکی عبارتند از:
• | قانون گاز ایده آل |
• | پنگ رابینسون |
• | پنگ رابینسون (توو) |
• | Soave-Redlich-Kwong |
• | Soave – Redlich – Kwong (Graboski – Daubert) |
• | آب (IAPWS) |
قانون گاز ایده آل
معادله قانون گاز ایده آل حالت است
(10-9)
همانطور که از نام آن پیداست، قانون گاز ایده آل فقط برای گازها قابل استفاده است. در واقع استفاده از آن محدود به گازهایی در فشارهای کم تا متوسط است.
پنگ رابینسون
معادله کلاسیک پنگ رابینسون (PR) حالت Ref. 5 توسط
(10-10)
کجا برای گونه های من ،
(10-11)
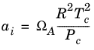
(10-12)
(10-13)
(10-14)
(10-15)
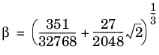
تابع آلفا، α i ، توسط
(10-16)
برای مخلوط ها
(10-17)
(10-18)
پارامترهای تعامل باینری (BIPs)، k PR ، متقارن با صفر در قطر هستند:
(10-19)
(10-20)
هنگامی که پارامترهای تعامل باینری در پایگاه داده برای مجموعه ای از گونه ها وجود ندارد، مقدار آن صفر می شود (یک گره هشدار ایجاد می شود). مقادیر دمای بحرانی، Tc ، فشار بحرانی، Pc و فاکتور غیرمرکز، ωi باید برای همه گونه ها مشخص شود .
پنگ رابینسون (توو)
برای اصلاح Twu ( مراجعه 6 ) از مدل پنگ-رابینسون، تابع آلفا، αi ، با
(10-21)
پارامترهای تعامل باینری k PR برای اصلاح Twu استفاده می شود. فاکتور غیرمرکز، ω i ، در این مدل استفاده نمی شود، اما دمای بحرانی و فشار بحرانی باید برای همه گونه ها مشخص شود. پارامترهای تناسب خاص گونه Li ، Mi ، Ni را می توان با برازش تعادل فاز گونه خالص به منحنی فشار بخار تعیین کرد .
Soave-Redlich-Kwong
معادله کلاسیک Soave–Redlich–Kwong حالت Ref. 7 توسط
(10-22)
با
(10-23)
و برای گونه های خالص i
(10-24)
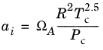
(10-25)
(10-26)
(10-27)
برای مخلوط ها
(10-28)
(10-29)
پارامترهای تعامل باینری، k SRK ، متقارن با صفر در قطر هستند:
(10-30)
(10-31)
اگر مقداری برای k SRK ,i,j در پایگاه داده وجود نداشته باشد، روی صفر تنظیم می شود (یک گره هشدار ایجاد می شود). مقادیر دمای بحرانی، Tc ، فشار بحرانی، Pc و فاکتور غیرمرکز، ωi ، باید برای همه گونه ها مشخص شود. معادله حالت Soave–Redlich–Kwong نسخه ای از معادله 10-22 است که توسط Soave Ref اصلاح شده است. 8 ، جایی که برای گونه های خالص i ، تابع آلفا به اصلاح می شود
(10-32)
Soave – Redlich – Kwong (Graboski – Daubert)
Ref Graboski and Daubert . 9 اصلاح معادله حالت Soave-Redlich-Kwong جایگزین تابع آلفا توسط
(10-33)
به جز H 2 که با آن جایگزین شده است
(10-34)
آب (IAPWS)
انجمن بین المللی خواص آب و بخار (IAPWS) مجموعه ای از همبستگی ها را برای محاسبه خواص آب در حالت های مختلف ارائه می دهد. همبستگی های موجود در COMSOL با نسخه ای به نام Industrial Formulation 1997 (IF-97) Ref. 10 – ر. 12 . همبستگی ها در محدوده های زیر معتبر هستند:
(10-35)
(10-36)
خواص آب و بخار زیر که با ایجاد ویژگی گونه در دسترس است، با استفاده از همبستگی های IAPWS محاسبه می شود: چگالی، حجم، آنتالپی، انرژی داخلی، انرژی هلمهولتز، ظرفیت گرمایی در فشار ثابت، و ظرفیت گرمایی در حجم ثابت. مقادیر موجود در فاز بخار و مایع را می توان با استفاده از یک محاسبه تعادل محاسبه کرد .
سایر پارامترها و خواص ترمودینامیکی موجود برای سیستم از پایگاه داده COMSOL ارائه شده است.
مدل های فاز مایع
مدل های ضریب فعالیت
مدلهای ضریب فعالیت برای توصیف مخلوطهای مایع در فشارها و دماهای کم تا متوسط که در آن معادلات حالت ناکافی است، استفاده میشود. هنگام استفاده از مدل های ضریب فعالیت، فوگاسیتی جزئی برای گونه i در فاز مایع به صورت تعریف می شود.
(10-37)
که بازده
(10-38)
که در آن ضریب فعالیت، γi ، فاز مایع غیر ایده آل را توصیف می کند و فوگاسیته در مرز فاز بخار-مایع در حالت تعادل برای گونه خالص i است . تصحیح Poynting، F i ، انحراف فوگاسیته گونه خالص از منحنی جوش را توصیف می کند و می تواند به صورت بیان شود.
(10-39)
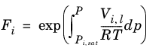
برای یک مایع تراکم ناپذیر، تقریبی از تصحیح Poynting را می توان مطابق با آن انجام داد
(10-40)
اصلاح Poynting اغلب برای فشار متوسط نادیده گرفته می شود. بنابراین، معادله 10-38 را می توان به صورت بیان کرد
(10-41)
اگر فاز بخار ایده آل در نظر گرفته شود،  معادله بالا به کاهش می یابد
معادله بالا به کاهش می یابد
(10-42)
در صورتی که فاز بخار ایده آل نباشد، می توان این کاهش را به صراحت انتخاب کرد.
تبدیل لگاریتمی معادله 10-38 به صورت زیر است:
(10-43)
راه حل ایده آل
برای یک راه حل ایده آل ضریب فعالیت برابر با یک است که به دست می آید:
(10-44)
راه حل منظم
معادله اسکاچارد-هیلدبراند Ref. 14 برای مخلوط غیر قطبی است
(10-45)
که در آن V i حجم مولی گونه و δ i پارامتر حلالیت گونه و δ av است
(10-46)
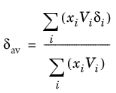
پارامتر حجم، V i ، برابر با حجم مایع، V i,l,b در نقطه جوش نرمال است که باید برای همه گونه ها مشخص شود. پارامتر حلالیت δ i باید برای همه گونه ها مشخص شود و می توان آن را از گرمای معمولی تبخیر، ΔH vap ،i و حجم مایع در نقطه جوش معمولی به صورت زیر تخمین زد:
(10-47)
راه حل منظم توسعه یافته
معادله توسعه یافته اسکاتچارد-هیلدبراند تصحیح فلوری و هاگینز را به مدل حل معمولی Ref. 16 :
(10-48)
جایی که
(10-49)
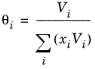
ویلسون
ویلسون Ref. 17 مدل ضریب فعالیت خود را از در نظر گرفتن احتمالات مولکول های همسایه در یک مایع به دست آورد.
(10-50)
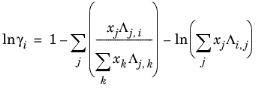
(10-51)
که در آن پارامتر حجم ویلسون، V w,i ، یک پارامتر خاص گونه است که حجم را توصیف می کند. اگر پارامتر حجم در دسترس نباشد، از حجم مایع در نقطه جوش معمولی استفاده می شود. پارامترهای برهمکنش باینری ویلسون λ i,j بر حسب دمای مطلق مشخص می شوند. ماتریس پارامتر برهمکنش باینری غیر متقارن و با صفر در قطر آن است. تمام مقادیر خارج از مورب باید مشخص شوند
(10-52)
(10-53)
NRTL
Renon و Prausnitz ( مراجعه 18 ) یک مدل ضریب فعالیت سه پارامتری را فرموله کردند که قادر به توصیف تعادل مایع-مایع است. مدل دو مایع غیر تصادفی (NRTL):
(10-54)
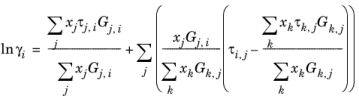
(10-55)
(10-56)
این سه پارامتر عبارتند از A i,j , Aj ,i و α i,j . یک فرم کلی تر در اینجا پیاده سازی می شود:
(10-57)
(10-58)
پارامترهای برهمکنش باینری، A i,j ، بر حسب دمای مطلق مشخص می شوند. مقادیر مورب صفر و ماتریس نامتقارن است. تمام مقادیر خارج از مورب باید مشخص شوند.
پارامترهای برهمکنش باینری، B i,j ، دارای مقادیر صفر در قطر هستند و ماتریس نامتقارن است. برای هر جفت گونه، حداقل A i,j یا B i,j باید مشخص شود.
پارامترهای تصادفی، α i,j دارای مقادیر صفر در قطر هستند و ماتریس متقارن است. تمام مقادیر خارج از مورب باید مشخص شوند. از طرف دیگر میتوان فرم عمومیتری را تنظیم کرد که مستقیماً پارامتر β i,j را مشخص کرد که مقادیر قطری آن صفر و ماتریس نامتقارن است. برای هر جفت گونه حداقل α i,j یا β i,j باید مشخص شود.
اگر مقداری برای این پارامترها در پایگاه داده وجود نداشته باشد، روی صفر تنظیم می شود (گره هشدار ایجاد می شود).
(10-59)
(10-60)
(10-61)
(10-62)
(10-63)
(10-64)
(10-65)
UNIQUAC
آبرامز و پراسنیتز مدل دو مایع دیگری به نام معادله شبه شیمیایی جهانی (UNIQUAC) را دنبال کردند (رجوع کنید به شماره 19 )، که بر اساس دو ضریب فعالیت فرموله شده است:
(10-66)
اولین عبارت این است که بخش ترکیبی به انرژی آزاد گیبس کمک می کند که از اثرات اندازه و شکل ناشی می شود.
(10-67)
و جمله دوم قسمت باقیمانده از فعل و انفعالات شیمیایی بین مولکول ها است،
(10-68)
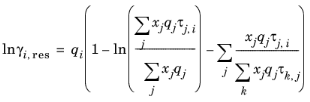
جایی که
(10-69)
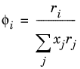
(10-70)
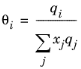
(10-71)
عدد هماهنگی برابر با z = 10 در نظر گرفته شده است . پارامترهای انرژی برهمکنش دوتایی، ΔE i,j ، بر حسب دمای مطلق (K) مشخص می شوند. مقادیر مورب صفر و ماتریس نامتقارن است. تمام مقادیر خارج از مورب باید مشخص شوند.
(10-72)
(10-73)
پارامترهای حجم، r i و پارامترهای سطح، q i پارامترهای مدل خاص برای هر گونه هستند. اگر پارامترها مشخص نشده باشند، می توان آنها را به ترتیب از حجم van derwaals، V VDW، i ، و area، A VDW، i استخراج کرد.
(10-74)
(10-75)
برای همه گونه های r i یا V VDW، i و q i یا A VDW، i باید مشخص شود.
یونیفک
ضرایب فعالیت گروه عملکردی UNIQUAC (UNIFAC؛ به مرجع 20 مراجعه کنید ) از معادلات مشابه UNIQUAC استفاده می کند، اما پارامترها از مشارکت گروه ساخته می شوند. اگر پارامترهای UNIQUAC برای همه گونه ها در دسترس نباشد، می توان از مدل استفاده کرد. ضرایب فعالیت از معادله 10-66 محاسبه می شود . بخش ترکیبی از معادله 10-67 ، که در آن
(10-76)
(10-77)
که در آن r k و q k مقادیر گروه k در گونه i هستند و ν k,i تعداد وقوع گروه k در مولکول است. عبارت باقیمانده در معادله 10-66 از جمع گروه های تابعی محاسبه می شود:
(10-78)
مقادیر ln( γk , res ) از مخلوطی که همه گونهها را در ترکیب مشخص x محاسبه میکند. مقادیر ln( γi ,k, res ) برای مخلوطی از گروه k با در نظر گرفتن تنها گونه های خالص i محاسبه می شود . هر دو برای گروه عملکردی k توسط تعریف می شوند
(10-79)
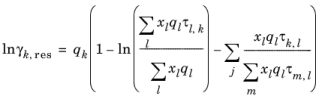
که در آن x l و x m ترکیبات گروه عاملی l و m در مخلوط هستند
(10-80)
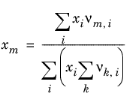
برای محاسبه فعالیت باقیمانده یک گونه خالص به دست می آوریم:
(10-81)
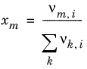
پارامترهای حجم r k و پارامترهای مساحت سطح q k پارامترهای مدل خاص برای هر گروه هستند. برهمکنش دوتایی بین گروه های k و m است
(10-82)
پارامترهای برهمکنش باینری، A k,m ، بر حسب دمای مطلق مشخص می شوند. مقادیر مورب صفر هستند، ماتریس نامتقارن است. تمام مقادیر خارج از مورب باید مشخص شوند.
گروه و پارامترهای تعاملی پیشفرض آنهایی هستند که توسط کنسرسیوم یونیفک منتشر شده است ( مرجع 21 تا مرجع 26 )، با گروههای اضافهشده از Balslev و Abildskov ( مرجع 27 ) اما میتوان آنها را در هر بسته یا پایگاه داده تغییر داد. گروه ها باید برای همه گونه ها مشخص شوند. توجه داشته باشید که ماتریس پارامتر تعامل پراکنده است و تنها در صورتی می توان از یک بسته استفاده کرد که تمام پارامترهای تعامل برای همه گروه های استفاده شده مشخص شده باشند.
چائو-سیدر (گریسون-استرید)
مدل Chao-Seader Ref. 13 ضرایب جزئی فاز مایع را برای گونه های خالص، برای استفاده از مخلوط هیدروژن و هیدروکربن در فشار و دماهای بالا مرتبط می کند. بیان می شود
(10-83)
این فعالیت بر اساس معادله اسکاتچارد-هیلدبراند Ref. 14 و در معادله 10-45 به معادله 10-47 ارائه شده است . مقادیر ویژه Chao-Seader برای حجم مایع، V i و پارامتر حلالیت، δ i استفاده می شود.
اگر V i مشخص نشده باشد، می توان آن را توسط
آ | حجم مولی در نقطه جوش نرمال |
ب | جلد واندروالس |
ج | از مدل راکت، معادله 10-80 ، در دمای نقطه جوش نرمال. |
اگر پارامتر حلالیت خاص Chao-Seader، δi ، مشخص نشده باشد، از پارامتر حلالیت عمومی استفاده می شود.
ضریب فوگاسیتی برای گونه های خالص i به صورت همبستگی است
(10-84)
(10-85)
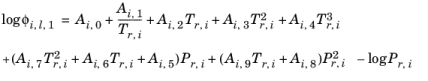
(10-86)
یک عامل غیر مرکزی خاص Chao-Seader ω i استفاده می شود. اگر ناشناخته باشد، می توان آن را برابر با ضریب غیر مرکزی عمومی قرار داد. مقادیر پارامتر از انتشارات بعدی Grayson و Streed Ref گرفته شده است. 15 و در جدول 10-2 آورده شده است .
H2 _ | CH 4 | دیگر | همه | ||
A i,0 | 1.50709 | 1.36822 | 2.05135 | A i,10 | -4.23893 |
A i,1 | 2.74283 | -1.54831 | -2.10899 | A i,11 | 8.65808 |
A i,2 | -0.02110 | A i,12 | -1.22060 | ||
A i,3 | 0.00011 | 0.02889 | -0.19396 | A i,13 | -3.15224 |
A i,4 | -0.01076 | 0.02282 | A i,14 | -0.02500 | |
A i,5 | 0.008585 | 0.10486 | 0.08852 | ||
A i,6 | -0.02529 | ||||
A i,7 | -0.00872 | ||||
A i,8 | -0.00353 | ||||
A i,9 | 0.00203 |
مدل فاز بخار مربوطه معادله حالت Redlich-Kwong است. مدل Chao-Seader (Grayson-Streed) زمانی معتبر است که
– | 255 K < T < 533 K |
– | P < 6.89 مگاپاسکال |
– | P r < 0.8 |
– | 0.5 < Tr ,i < 1.3، برای همه هیدروکربن ها به جز CH 4 |
– | x CH4 < 0.3 |
– | برای سیستمی که شامل CH 4 یا H 2 S است: |
آنتالپی، آنتروپی و انرژی آزاد گیبس را می توان از معادله 10-109 تا معادله 10-118 محاسبه کرد .
مدل های حجم مایع
هنگامی که یک مدل ضریب فعالیت یا مدل Chao-Seader (Grayson-Streed) استفاده می شود، یک مدل حجم مایع باید به صراحت انتخاب شود. همچنین زمانی که از معادله حالت استفاده می شود، می توان مدل حجم مایع را اختصاص داد.
برای مایعات، چگالی به صورت متقابل حجم مایع تعریف می شود:
(10-87)
با استفاده از یک معادله حالت مکعبی، راه حل دارای 1، 2 یا 3 ریشه مختلف برای حجم است. چگالی مایع به عنوان ریشه ای که بیشترین چگالی را تولید می کند و چگالی بخار به عنوان ریشه ای که کمترین چگالی را تولید می کند، تعریف می شود.
معادله حالت
هنگامی که یک معادله حالت به عنوان مدل فاز مایع انتخاب می شود، حجم مایع به طور پیش فرض تنظیم می شود تا با استفاده از همان معادله مدل حالت محاسبه شود. سایر مدل های حجم مایع؛ Ideal Mixture ، COSTALD و Rackett نیز موجود است.
توجه داشته باشید، مدل فاز بخار و حجم مایع نمی توانند از معادله های مختلف مدل های حالت استفاده کنند.
مخلوط ایده آل
برای یک مخلوط ایده آل، حجم مایع از چگالی گونه های خالص (مرتبط با چگالی مایع اشباع) محاسبه می شود:
(10-88)
در این مورد، چگالی گونههای خالص با چگالی مایع اشباع مطابقت دارد، که به عنوان یک همبستگی وابسته به دما برای همه گونهها در پایگاه داده داخلی موجود است.
COSTALD
Hankinson and Thomson Ref. 28 معادله چگالی مایع ایالات مربوطه (COSTALD) را به عنوان ارائه کرد
(10-89)
(10-90)
(10-91)
(10-92)
(10-93)
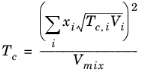
(94-10)
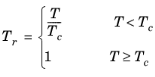
(10-95)
که در آن حجم، V i و عامل غیر مرکزی، ω i برای گونه i پارامترهای خاص مدل هستند. اگر پارامتر حجم COSTALD مشخص نشده باشد، از حجم واندروالس زمانی که V VDW، i > 0.3 × 10 -3 m3 / mol تخمین زده می شود
(10-96)
در غیر این صورت، می توان آن را برابر با حجم بحرانی به عنوان تنظیم کرد
(97-10)
اگر ضریب غیر مرکزی COSTALD، ω i مشخص نشده باشد، می توان آن را برابر با ضریب غیر مرکزی عمومی برای گونه i قرار داد . دمای بحرانی Tc ,i باید برای همه گونه ها مشخص شود.
مقادیر پارامتر همبستگی عبارتند از:
a | -1.52816 | ه | -0.296123 |
b | 1.43907 | f | 0.386914 |
g | -0.81446 | g | -0.0427258 |
d | 0.190454 | ساعت | -0.0480645 |
راکت
معادله راکت Ref. 29 چگالی مایع را در نقطه اشباع محاسبه می کند و می تواند برای توصیف چگالی مایع در هر فشاری با این فرض که مایع تراکم ناپذیر است استفاده شود. معادله و شرایط آن را می توان به صورت زیر بیان کرد:
(98-10)
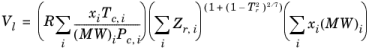
(10-99)
(10-100)
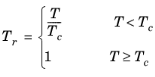
دماهای بحرانی، Tc ،i ، فشارهای بحرانی، Pc ،i ، و وزنهای مولکولی، Mi ، باید برای همه گونهها مشخص شوند. پارامتر مدل، Z r,i ، باید برای همه گونه ها مشخص شود. اگر مقدار در دسترس نباشد، می توان آن را روی ضریب تراکم پذیری بحرانی تنظیم کرد:
(10-101)




