امپدانس انتقال یک مرز داخلی به عنوان نسبت افت فشار در سراسر مرز به سرعت عادی در مرز تعریف می شود:
(2-35)
مقدار حاصل از Z n را می توان به عنوان برهم نهی از چندین مشارکت که به طور جداگانه مشتق شده اند در نظر گرفت. توجه داشته باشید که تئوری زیر فقط برای سوراخ هایی با سوراخ های دایره ای شکل معتبر است. انواع دیگر سوراخ ها می توانند به نتایج بسیار متفاوتی منجر شوند که مدل هایی را که در اینجا در نظر گرفته شده اند ناکافی و غیر قابل اعتماد می کند.
امپدانس انتقال یک سوراخ
اجازه دهید محور مختصات z در امتداد محور یک سوراخ استوانه ای به ارتفاع t p هدایت شود ( شکل 2-15 را ببینید ). اجازه دهید تغییر فشار و سرعت در امتداد محور z دارای الگوی زیر باشد:
(2-36)
جایگزینی معادله 2-36 به معادله 2-35 نتیجه می دهد
که در آن Zc امپدانس مشخصه و kc عدد موج مختلط است که با توجه به مدلهای فرکانس کاهشیافته کم (LRF) از آکوستیک ناحیه باریک برای شکافها، مجراهای دایرهای، کانالهای مستطیلی و مجرای مثلثی متساوی الاضلاع تعریف شده است . به این معنا که،
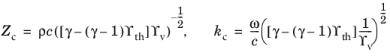 .
.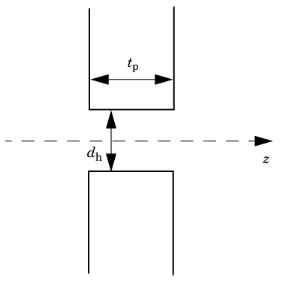
شکل 2-15: به اشتقاق امپدانس انتقال یک سوراخ یک سوراخ.
عبارت امپدانس انتقال نرمال شده یک روزنه خوانده می شود
(2-37)  .
.
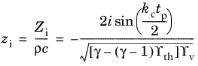 .
.برای صفحات نازک تر (  ) تقریب
) تقریب  معتبر است که نتیجه می دهد
معتبر است که نتیجه می دهد
(2-38)  .
.
توجه داشته باشید که معادله 2-38 منطبق بر عبارتی است که از فرمول کراندال برای یک لوله بی نهایت با مقطع دایره ای به دست می آید (رجوع کنید به شماره 35 ). معادله 2-37 هم اثرات چسبناک و هم اثرات حرارتی را در داخل سوراخ نشان می دهد، در حالی که معادله 2-38 ساده شده فقط شامل بخش چسبناک است (اثرات حرارتی برای حد صفحه نازک ناچیز است).
منقبض ورید و تخلخل ناحیه
معادله 2-37 و معادله 2-38 در صورتی دقیق هستند که خطوط جریان یک جریان از طریق سوراخ موازی با محور z در سراسر ناحیه روزنه باشد. در واقع یک جزء شعاعی جریان وجود دارد که منجر به کاهش (انقباض) این ناحیه می شود. حداقل ناحیه ای که در آن خطوط جریان موازی با محور z باقی می مانند، vena contracta نامیده می شود. سرعت جریان در ورید انقباض نیز با سرعت جریان ایده آل متفاوت است. ضریبی که این اثرات را محاسبه می کند، ضریب تخلیه، C D نامیده می شود . مقدار ضریب تخلیه را می توان از اندازه گیری ها به عنوان تابعی از ضخامت صفحه و شکل و قطر روزنه به دست آورد.
پارامتر دیگری که برای بیان امپدانس داخلی یک سوراخ استفاده می شود تخلخل، σ است . سوراخ ها معمولاً به طور یکنواخت روی صفحه توزیع می شوند و تخلخل توزیع را به عنوان نسبت ناحیه توخالی به مساحت صفحه محاسبه می کند. بسته به الگوی مورد استفاده در هنگام پخش شدن سوراخ ها روی صفحه، تخلخل به صورت زیر تعریف می شود.
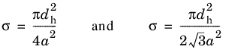
به ترتیب برای یک الگوی مربع و مثلثی. پارامتر a فاصله سوراخ ها را تعیین می کند.
عبارت بدست آمده برای امپدانس داخلی یک سوراخ از تقسیم z i بر حاصلضرب σ C D بدست می آید :
(2-39)  .
.
از معادله 2-37 یا معادله 2-38 می توان برای جایگزینی z i در معادله 2-39 استفاده کرد . مدل های به دست آمده به ترتیب به عنوان مدل های صفحه ضخیم و نازک شناخته می شوند.
تصحیح پایان و تعامل سوراخ- سوراخ
زیرمجموعه “روزنه” در معادله 2-39 به این معنی است که عبارت امپدانس انتقال یک سوراخ ناشی از وجود سوراخ ها را محاسبه می کند. یعنی یک پیستون سیال به طول t p . با این حال، جرم واقعی سیال تحت تاثیر یک موج فرودی بزرگتر از جرم درون سوراخ است. جرم موثر سیال را می توان توسط پیستونی در نظر گرفت که در هر طرف به نسبت δ از پیستون اولیه بلندتر است ( شکل 2-16 را ببینید ). این منجر به اضافه کردن دو عبارت اضافی (برای هر طرف سوراخ) از شکل معادله 2-38 می شود که t p جایگزین آن با δ . انتخاب معادله 2-38به دلیل عدم وجود دیوارهای با رسانایی بالا در ناحیه اصلاحات انتهایی است.
اگر دو سوراخ نسبتاً نزدیک به یکدیگر قرار گیرند، توده های واقعی سیال متصل می توانند همپوشانی داشته باشند. این باعث میشود که جرم کل کمتر از مجموع جرمهای سوراخ جداگانه باشد. به منظور در نظر گرفتن اندرکنش سوراخ- سوراخ، تصحیح انتهایی با یک ضریب f int کاهش می یابد .
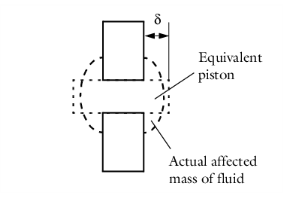
شکل 2-16: به تعریف اصلاحات پایانی.
آخرین تابعی از تخلخل است و اغلب با تابع Fok بیان می شود:
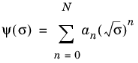 .
.تصحیح انتهایی معمولاً تابعی از قطر سوراخ در نظر گرفته می شود و در عمل می تواند برای قسمت های مقاومتی و راکتیو امپدانس انتقال متفاوت باشد. به همین دلیل، تقسیم δ به دو بخش مفید است: δ مقاومت و δ واکنش . عبارت حاصل که تصحیح انتهایی و برهمکنش سوراخ-حفره را به حساب می آورد، خوانده می شود
(2-40)  .
.
معادله 2-40 تنها در صورتی قابل قبول است که رسانه در هر دو طرف سوراخ یکسان باشد. اگر صفحه توسط یک لایه متخلخل در یک طرف پشتیبان باشد، مقادیر δ و f int می تواند به طور قابل توجهی با مقادیر در سمت دیگر متفاوت باشد. به عنوان مثال، برهمکنش بین سوراخ ها توسط محیط متخلخل مختل می شود، که منجر به نادیده گرفتن f int در یک طرف صفحه می شود و منجر به ضریب تصحیح زیر می شود: (δ + 1 ) f int . |
اثرات غیر خطی و جریان متوسط
در سطوح فشار صوتی متوسط و بالا، جابجایی ذرات آکوستیک با قطر سوراخ ها قابل مقایسه می شود. این امر باعث جدا شدن جریان و ریزش گرداب در ورودی و خروجی سوراخ می شود. این منجر به اتلاف انرژی صوتی و افزایش مقاومت آکوستیک سوراخ شده Ref. 36 . یعنی یک عبارت مقاومت اضافی باید به عبارت امپدانس انتقال حاصل اضافه شود.
اشکال مختلف کمک به مقاومت به معنای زیر مشابه است:
• | عبارت مقاومت مستقیماً با سرعت ذرات صوتی متناسب است که آن را غیرخطی می کند. |
• | این اصطلاح از طریق سرعت ذرات صوتی وابسته به فرکانس است. |
عبارت گنجانده شده در شرایط مرزی صفحه سوراخ شده داخلی نشان می دهد
(2-41)  ،
،
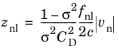 ،
،که در آن f nl یک ضریب تصحیح است (به طور پیش فرض برابر با 1 ) و v n مولفه سرعت ذرات صوتی نرمال به صفحه است. عبارات دیگر برای عبارت مقاومت غیرخطی را می توان در Ref. 36 .
وجود یک جریان متوسط نیز امپدانس انتقال را تغییر می دهد. به منظور در نظر گرفتن این و سایر اثرات احتمالی، ویژگی شرط مرزی صفحه سوراخدار داخلی گزینهای را برای فعال کردن مقاومت و راکتانس تعریفشده توسط کاربر دارد:
(2-42)  .
.
نسبت به جریان متوسط، سهم یک چرا یا یک جریان بایاس در مقاومت را می توان از طریق عدد ماخ جریان بیان کرد که در Ref نشان داده شده است. 37 .
ترکیب عبارات معادله 2-39 – معادله 2-42 با هم عبارت کاملی را برای امپدانس انتقال یک سوراخ برای ضخامت به دست می دهد.
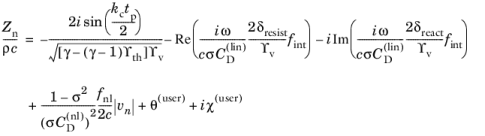
و لاغر
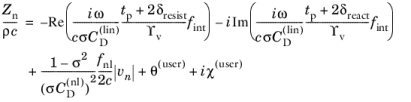
مدل های بشقاب ضریب دبی C D برای بخش خطی و غیرخطی به دلیل انعطاف پذیری متفاوت است.




