محاسبه شدت پرتو با تغییر محاسبات Intensity به Compute intensity یا Compute intensity در رسانه های درجه بندی شده در پنجره تنظیمات برای رابط Ray Acoustics امکان پذیر است. گزینه های Compute intensity and power و Compute intensity and power در رسانه های درجه بندی شده نیز می توانند برای محاسبه شدت استفاده شوند، با تنها تفاوت این که این گزینه ها یک متغیر وابسته کمکی اضافی برای کل توان انتقال یافته توسط پرتو تعریف می کنند. تنظیم شدت محاسبه قوی تر و دقیق تر از محاسبه شدت در رسانه های درجه بندی شده است ، اما فقط برای رسانه های همگن قابل استفاده است. تنظیم شدت را در رسانه های درجه بندی شده محاسبه کنیدمی تواند برای رسانه های همگن و درجه بندی شده استفاده شود، اما خطای عددی بیشتری نسبت به شدت محاسبه ایجاد می کند .
مفروضاتی برای شدت محاسبات در رسانه های همگن
هنگامی که Compute Intensity انتخاب می شود، شدت پرتو در امتداد هر مسیر پرتو با استفاده از مفروضات زیر محاسبه می شود:
1 | جبهه موجی که توسط هر پرتو نشان داده میشود، یک زاویه صفحه ثابت (2D) یا زاویه جامد (3D) دارد، که تنها زمانی میتواند تغییر کند که پرتوها در مرزها منعکس یا شکست شوند. |
2 | با توجه به شعاع انحنا در دو موقعیت در یک دامنه و شدت در یکی از این دو موقعیت، شدت در موقعیت دیگر را می توان با استفاده از رابطه محاسبه کرد. |
3 | به جز زمانی که پرتوها در مرزها منعکس یا شکست می شوند، شعاع اصلی انحنا با سرعت ثابت تغییر می کند: |
4 | جهت انحنای اصلی تغییر نمی کند، مگر زمانی که پرتوها در مرزها منعکس یا شکسته شوند. |
این مفروضات در رسانه های درجه بندی شده، که در آن سرعت صوت به طور مداوم به عنوان تابعی از موقعیت تغییر می کند، معتبر نیستند. این امکان وجود دارد که زاویه بین دو پرتو مختلف با انتشار آنها در محیط تغییر کند، بنابراین زاویه جامد تحت تأثیر جبهه موج دیگر ثابت نیست. در نتیجه، شدت پرتو را نمی توان با استفاده از نسبت شعاع اولیه و نهایی انحنای اصلی بیان کرد.
تعریف تانسور انحنای در رسانه های درجه بندی شده
محاسبه شدت پرتو در محیط های درجه بندی شده بر اساس مفهوم تانسور انحنای K است که بر حسب انحناهای اصلی κ1 و κ2 و جهات انحنای اصلی متناظر e1 و e2 تعریف شده است :
از آنجایی که e 1 و e 2 متعامد هستند، نتیجه می شود که κ 1 و κ 2 مقادیر ویژه K هستند . همچنین نتیجه می شود که K مفرد است زیرا هیچ سهمی متعامد برای e 1 و e 2 وجود ندارد .
نشانه های انحنای اصلی به گونه ای انتخاب می شوند که انحنای مثبت نشان دهنده همگرا شدن جبهه موج باشد، در حالی که انحنای منفی نشان دهنده واگرا شدن جبهه موج است.
انتخاب سیستم مختصاتی که در آن تانسور انحنای تعریف شده است بسیار مهم است. توصیف سیستم مختصات به گونه ای راحت است که دو محور مختصات در صفحه حاوی e 1 و e 2 قرار گیرند ، زیرا این باعث کاهش تعداد جمله های غیر صفر در K می شود . اگر بتوان K را در یک سیستم مختصاتی که در آن e 1 و e 2 در آن تعریف شود ، می توان به کاهش بیشتر تعداد عبارت های غیر صفر دست یافت.بردارهای پایه هستند. این در دو بعدی امکان پذیر است زیرا یکی از جهات انحنای اصلی همیشه با جهت خارج از صفحه موازی است، اما در سه بعدی امکان پذیر نیست زیرا جهات انحنای اصلی می توانند با انتشار پرتوها در یک محیط درجه بندی شده تغییر کنند.
در کلیترین حالت سه بعدی، تانسور انحنای با استفاده از نمادهای زیر توصیف میشود، که هر کدام از آنها با مبنای متعارف متفاوتی مطابقت دارد:
• | K X : تانسور انحنای تعریف شده در سیستم مختصات دکارتی با بردارهای پایه x ، y ، و z . |
• | K W : تانسور انحنای تعریف شده در سیستم مختصات متشکل از دو جهت انحنای اصلی e 1 و e 2 و جهت انتشار t . |
• | KS : تانسور انحنای تعریف شده در سیستم مختصاتی که در آن یک بردار پایه جهت انتشار t است . دو بردار پایه دیگر s 1 و s 2 را می توان به طور دلخواه تعیین کرد، تا زمانی که آنها متعامد با یکدیگر و به t باشند ، به طوری که |
بردارهای پایه s 1 و s 2 به صورت زیر تعریف می شوند:
برای جلوگیری از قطب ها در تعریف بردارهای پایه، تعاریف جایگزین زیر زمانی که پرتوها تقریباً موازی با محور z منتشر می شوند استفاده می شود :
رابطه بین s 1 , s 2 , e 1 و e 2 با استفاده از
که در آن زاویه چرخش  یک متغیر وابسته کمکی است که برای هر پرتو ذخیره می شود.
یک متغیر وابسته کمکی است که برای هر پرتو ذخیره می شود.
رابطه بین K S و K W توسط
که در آن Q 0 ماتریس چرخش است:
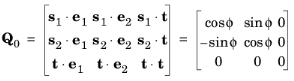
رابطه بین K X و K S توسط
که در آن Q ماتریس چرخش است:
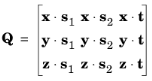
در دوبعدی، یکی از جهات انحنای اصلی همیشه مشخص است، بنابراین می توان s 1 و s 2 را طوری تعریف کرد که با e 1 و e 2 منطبق باشند. ماتریس چرخش Q 0 هویت است و متغیر وابسته کمکی برای زاویه را  می توان حذف کرد.
می توان حذف کرد.
مشتقات تانسور انحنای
به دنبال ر. 3 ، مشتق تانسور انحنا در امتداد مسیر پرتو در یک محیط درجه بندی شده با عبارت داده می شود
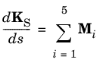
که در آن عبارات M i با روش های مختلفی مطابقت دارد که انحنا می تواند به خواص محیط بستگی داشته باشد. آنها با استفاده از عبارات زیر تعریف می شوند:
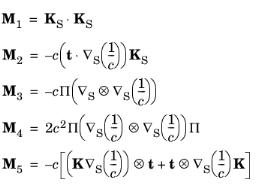
جایی که Π ماتریس طرح ریزی است:
عملگر گرادیان ∇ S شامل مشتقاتی است که با توجه به مختصات محلی با بردارهای پایه s 1 , s 2 و t گرفته می شوند .
مشتقات انحنای اصلی
با اعمال قانون زنجیره، مشتقات عناصر غیر صفر KS را می توان بر حسب انحناهای اصلی که عناصر مورب KW و زاویه چرخش را اشغال می کنند بیان کرد :
تثبیت عددی
انحناهای اصلی κ1 و κ2 گزینههای ایدهآلی برای متغیرهای وابسته کمکی ذخیرهشده توسط هر پرتو نیستند، زیرا مقادیر آنها میتواند بهطور دلخواه با نزدیک شدن پرتوها به کاستیک بزرگ شود . به طور مشابه، شعاعهای اصلی انحنای r 1 و r 2 گزینههای ایدهآلی نیستند زیرا زمانی که جبهه موج واگرا شروع به همگرا شدن میکند در حالی که در یک محیط درجهبندی شده منتشر میشود، مقادیر آنها میتواند به طور دلخواه بزرگ شود.
در عوض، متغیرهای وابسته کمکی ذخیره شده توسط هر پرتو، متغیرهای کمکی α1 و α2 هستند . در دوبعدی، تنها یک متغیر کمکی تخصیص داده میشود، زیرا شعاع اصلی انحنای خارج از صفحه بینهایت فرض میشود. انحناهای اصلی بر حسب متغیرهای کمکی با استفاده از عبارت بیان می شوند
که در آن κ 0 = 1 1/m و i ∈ [ 1 , 2 ] . سپس مشتقات با عبارت مرتبط می شوند
به طور مشابه، شدت ممکن است در سوزاننده بی نهایت بزرگ شود، و متقابل آن بی نهایت بزرگ می شود، زیرا پرتوها تحت تضعیف قرار می گیرند، بنابراین یک متغیر کمکی Γ برای نشان دادن شدت پرتو استفاده می شود:
جایی که من 0 = 1 وات بر متر مربع . رابطه بین متغیر کمکی شدت پرتو و انحناهای اصلی است
که α ضریب تضعیف محیط است.




