تمام رابطهای PDE و فرمهای معادله از چندین متغیر وابسته پشتیبانی میکنند – یعنی سیستمی از PDEها که میتوانند جفت شوند.
فرم عمومی سیستم PDE
در مورد چندین متغیر وابسته u 1 , u 2 , …, u N , یک سیستم فرمی کلی از معادلات به شکل زیر است:
(16-4)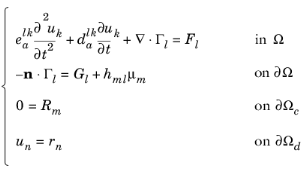
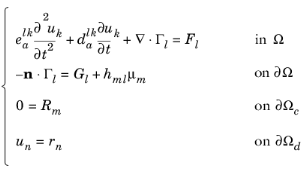
شاخص معادله l و k از 1 تا N متغیر است ، در حالی که شاخص محدودیت عمومی m از 1 تا Mc و شاخص شرط دیریکله n از 1 تا Md متغیر است . بنابراین تعداد کل محدودیت ها M = M c + M d است . این بحث از قرارداد جمع استفاده می کند. Fl ، Gl ، Rm ، و rn اسکالر هستند، در حالی که Γl یک بردار فضایی است. جرم و ضرایب میرایی e a و d a ماتریس های N – به – N هستند ، در حالی که نیروی محدودیت ژاکوبین h یک ماتریس M -by- N است. توجه داشته باشید که چندین ضریب لاگرانژ وجود دارد: μ 1 , μ 2 ,…, μ M .
برای فرم فشرده تر، اجازه دهید u بردار با مولفه های u k باشد ، اجازه دهید Γ ماتریسی با مولفه های Γlj و غیره باشد. سپس سیستم معادلات به همان شکلی که در معادله 1-16 برای یک متغیر وابسته منفرد داده شده است به خود می گیرد.
همچنین می توان سیستم را به طور کامل بر روی فرم مؤلفه نوشت، جایی که Γlj اجزای بردار Γl و n j جزء بردار عادی n هستند . سپس سیستم معادلات تبدیل می شود:
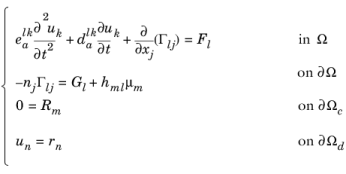
سیستم برای دو متغیر در فرم کلی
مثال زیر از یک PDE به شکل کلی یک سیستم ثابت برای N = 2 جزء محلول در n = 2 بعد فضا با محدودیت M = 2 است:
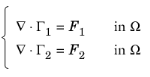
با شرایط مرزی تعمیم یافته نویمان
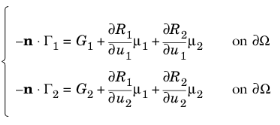
و شرایط مرزی دیریکله
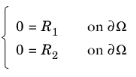
|
|
|
سیستم معادلات فرم ضریب
شکل ضریب یک سیستم معادله با N متغیرهای وابسته u 1 , u 2 , …, u N را می توان به راحتی از شکل عمومی PDE نشان داده شده در معادله 16-4 با استفاده از جایگزینی بدست آورد:
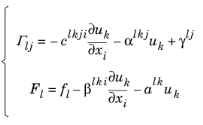
جایی که شاخص k و l روی متغیرهای وابسته از 1 تا N تشکیل میشوند ، در حالی که شاخص i و j روی ابعاد فضایی از 1 تا K قرار میگیرند . این بدان معنی است که برای سیستم معادلات با N متغیر وابسته در ابعاد K فضا، ضرایب دارای اندازه های زیر هستند:
|
•
|
e a یک ماتریس N – به – N است
|
|
•
|
d a یکماتریس N – به – N است
|
|
•
|
c یکآرایه چهار بعدی N -by- N -by- K -by- K است
|
|
•
|
α یکآرایه سه بعدی N – در – N – با K است
|
|
•
|
β یکآرایه سه بعدی N – در – N – با K است
|
|
•
|
a یک ماتریس N – به – N است
|
|
•
|
f یکبردار N است
|
|
•
|
g یکبردار N است
|
|
•
|
q یکماتریس N – به – N است
|
سیستم برای دو متغیر در فرم ضریب
با دو متغیر وابسته u 1 و u 2 ، مسئله PDE ثابت به شکل ضریب به سیستم معادله زیر منجر می شود:
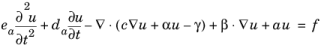
جایی که u = ( u 1 , u 2 ) . اصطلاح توده به این صورت تعریف می شود
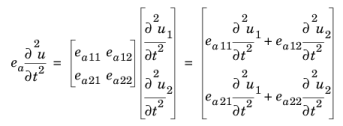
به طور مشابه، اصطلاح میرایی است
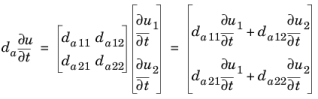
با این حال، اگر ea = 0 باشد ، d a اغلب ضریب جرم نامیده می شود.
شار انتشاری به این صورت تعریف می شود
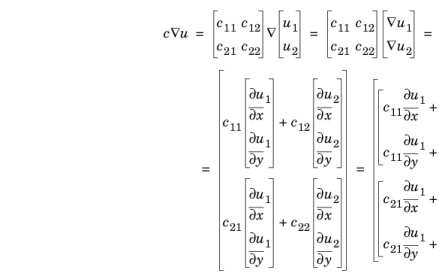
بردارهای ستونی کجا 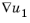 و هستند.
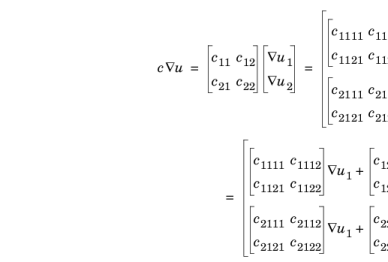
و هستند. 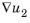 ماتریس شار یا تانسور شار یک بردار ستونی در این ارائه است. برای مواد ناهمسانگرد، اجزای c 11 , c 12 , c 21 و c 22 می توانند ماتریس هایی باشند که در بالا برای ضریب تک متغیری از PDE توضیح داده شد. در این حالت، شار انتشاری خوانده می شود
ماتریس شار یا تانسور شار یک بردار ستونی در این ارائه است. برای مواد ناهمسانگرد، اجزای c 11 , c 12 , c 21 و c 22 می توانند ماتریس هایی باشند که در بالا برای ضریب تک متغیری از PDE توضیح داده شد. در این حالت، شار انتشاری خوانده می شود
شار همرفتی محافظه کارانه به صورت تعریف می شود

در اینجا سومین شاخص، k ، α ijk با پسوندهای مختصات فضایی x و y مطابقت دارد .
منبع شار محافظه کارانه به صورت تعریف شده است
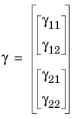
در اینجا دومین اندیس، j ، γ ij، پسوند مختصات فضایی x و y را نشان می دهد.
برای شرایط شار، عملگر واگرایی روی هر ردیف به طور جداگانه کار می کند. برای نشان دادن این موضوع، واگرایی منبع شار محافظه کارانه را در نظر بگیرید
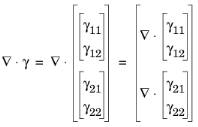
اصطلاح همرفت به این صورت تعریف می شود
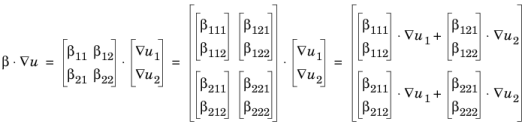
نام متغیر این مؤلفه ها beu1 و beu2 است .
اصطلاح جذب به این صورت تعریف می شود
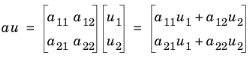
نام متغیرهای این مؤلفه ها au1 و au2 است .
اصطلاح منبع به این صورت تعریف می شود
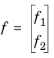
نام متغیرهای این مؤلفه ها f1 و f2 است .
شرایط مرزی
شرط مرزی دیریکله، به شکل گسترش یافته، نشان می دهد
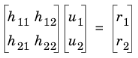
اگر شرط دیریکله را انتخاب کنید، شرط مرزی تعمیم یافته نویمان را نیز دریافت می کنید که به عنوان خوانده شده است
بردار نرمال n = ( n x , n y ) بر روی بردار شار به همان روش عملگر واگرایی که قبلا توضیح داده شد عمل می کند. اگر h دارای رتبه کامل باشد (مثلاً مانند ماتریس هویت پیشفرض)، فقط محدودیتهای شرط دیریکله فعال هستند.
اگر شرط نویمان را انتخاب کنید، فقط شرط مرزی را دریافت می کنید
جزء نرمال شار انتشاری به این صورت تعریف می شود
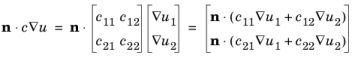
جزء نرمال شار همرفتی محافظه کارانه به این صورت تعریف می شود
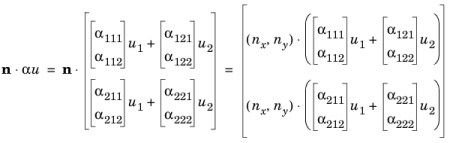
جزء نرمال منبع شار محافظه کارانه به این صورت تعریف می شود
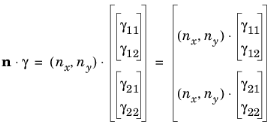
اصطلاح جذب مرزی به این صورت تعریف می شود
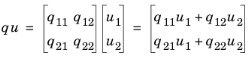
اصطلاح منبع مرزی به این صورت تعریف می شود
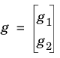
|
|
|




