آکوستیک فیزیک صدا است. صدا همانگونه که توسط گوش تشخیص داده می شود، احساس تغییرات سریع بسیار کوچک در فشار آکوستیک p در بالا و پایین یک مقدار ساکن p 0 است . این مقدار استاتیک فشار اتمسفر (حدود 100000 پاسکال) است.
دامنه تغییرات فشار کوچکی که می تواند توسط گوش انسان تشخیص داده شود، از تقریباً 2·10 -5 Pa در آستانه شنوایی تا 20 Pa برای صدای موتور جت متغیر است. دامنه در سطوح گفتار معمولی حدود 0.02 Pa است. دامنه های توصیف شده در اینجا اغلب در مقیاس دسی بل لگاریتمی، نسبت به مقدار آستانه شنوایی 2·10 -5 Pa، در واحد دسی بل SPL ارائه می شوند.
تغییرات فشار آکوستیک معمولاً به عنوان امواج فشار منتشر شده در فضا و زمان توصیف می شود. تاج های موج حداکثر فشار هستند در حالی که فرورفتگی ها نشان دهنده حداقل فشار هستند.
به عبارت کلی تر، صدا زمانی ایجاد می شود که سیال توسط منبعی مختل شود. به عنوان مثال یک جسم ارتعاشی، مانند مخروط بلندگو در یک سیستم صوتی. هنگامی که یک مخروط بلندگوی باس صدا را با فرکانس بسیار پایین تولید می کند، می توان حرکت آن را مشاهده کرد. همانطور که مخروط به سمت جلو حرکت می کند، هوای جلوی خود را فشرده می کند و باعث افزایش فشار هوا می شود. سپس از حالت استراحت خود به عقب بر می گردد و باعث کاهش فشار هوا می شود. این روند ادامه می یابد و موجی از فشار متناوب بالا و پایین را با سرعت صوت تابش می کند.
فرکانس f (واحد SI: هرتز = 1/s) تعداد ارتعاشات (پیک فشار) درک شده در ثانیه و طول موج λ (واحد SI: m) فاصله بین دو چنین پیک است. سرعت صوت c (واحد SI: m/s) به عنوان حاصل ضرب فرکانس و طول موج، c = λ f . اغلب برای تعریف فرکانس زاویه ای ω (واحد SI: راد/ثانیه) موج، که ω = 2 π f است ، و فرکانس را به یک تغییر فاز کامل 360 o مرتبط می کند، راحت است. عدد موج k (واحد SI: rad/m) به صورت k = 2 π / λ تعریف می شود. عدد موج، که تعداد امواج در یک فاصله خاص است، معمولاً به عنوان بردار k تعریف می شود ، به طوری که حاوی اطلاعاتی در مورد جهت انتشار موج است، با | k | = k به طور کلی، رابطه بین فرکانس زاویه ای ω و عدد موج k را رابطه پراکندگی می نامند. برای سیالات ساده ω / k = c است .
معادلات حاکم
معادلاتی که انتشار صوت در سیالات را توصیف می کند از معادلات حاکم بر جریان سیال به دست آمده است. یعنی بقای جرم که با معادله پیوستگی توصیف می شود. بقای تکانه، که اغلب به عنوان معادلات ناویر-استوکس شناخته می شود. معادله بقای انرژی؛ معادلات سازنده مدل؛ و یک معادله حالت برای توصیف رابطه بین متغیرهای ترمودینامیکی. در مورد کلاسیک آکوستیک فشار، که بیشتر پدیدههای صوتی را به دقت توصیف میکند، جریان بدون تلفات و آدیاباتیک فرض میشود، اثرات ویسکوز نادیده گرفته میشوند و از یک معادله حالت ایزنتروپیک خطی استفاده میشود.
تحت این مفروضات، میدان صوتی با یک متغیر، فشار p (واحد SI: Pa) توصیف میشود و توسط معادله موج کنترل میشود.
جایی که t زمان (واحد SI: s)، ρ 0 چگالی سیال (واحد SI: kg/m 3 )، و c سرعت (آدیاباتیک) صوت (واحد SI: m/s) است.
مشکلات صوتی اغلب شامل امواج هارمونیک ساده مانند امواج سینوسی است. به طور کلی، هر سیگنالی ممکن است از طریق سری فوریه به اجزای هارمونیک گسترش یابد. سپس معادله موج را می توان در حوزه فرکانس برای یک فرکانس در یک زمان حل کرد. یک راه حل هارمونیک شکل دارد
جایی که مؤلفه های p ( x ) و sin زمانی ( ω t ) تقسیم می شوند. فشار ممکن است به روشی کلی تر با استفاده از متغیرهای پیچیده نوشته شود
(1)
که در آن مقدار فیزیکی واقعی (آنی) فشار، بخش واقعی معادله 1 است . با استفاده از این فرض برای میدان فشار، معادله موج وابسته به زمان به معادله معروف هلمهولتز کاهش مییابد.
(2)
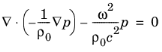
در حالت همگن، یک راه حل ساده برای معادله هلمهولتز ( معادله 2 ) موج صفحه است.
(3)
که در آن P 0 دامنه موج است و در جهت k با فرکانس زاویه ای ω و عدد موج k = | k |.
در بیشتر موقعیت های عملی، راه حل تحلیلی دقیقی برای معادله 2 وجود ندارد. حل معادله نیاز به یک رویکرد عددی با استفاده از شبیه سازی دارد.
روشهای عددی
همانطور که گفته شد، حل معادلات حاکم برای مسائل صوتی به صورت تحلیلی – مانند معادله هلمهولتز ( معادله 2 ) – فقط در چند موقعیت ساده امکان پذیر است. برای حل مسائل صنعتی در زندگی واقعی، که به خوبی می توانند مسائل چندفیزیکی شامل چندین فیزیک جفت شده باشند، روش های عددی ضروری است. این کار COMSOL Multiphysics است. در ماژول آکوستیک، بیشتر رابط های فیزیک بر اساس روش اجزای محدود (FEM) هستند. به منظور گسترش دامنه مدلهای قابل حل، ماژول آکوستیک همچنین شامل آکوستیک فشار، رابط عناصر مرزی مبتنی بر BEM، دو رابط مبتنی بر روش گالرکین ناپیوسته (dG-FEM) و آکوستیک پرتو است که از پرتو استفاده میکند. روش ردیابی
حل یک مدل با استفاده از FEM نیازمند یک شبکه محاسباتی است. راه حل بر روی هر عنصر مش (عناصر محدود) توسط یک تابع شکل (یک مبنای محلی یا تابع درون یابی) تقریبی می شود. راه اندازی این سیستم از عناصر مش و توابع شکل محلی منجر به یک مشکل ماتریس برداری گسسته می شود که باید حل شود. پس از حل مسئله ماتریسی با روش مناسب، می توان راه حل مسئله اصلی را بازسازی کرد. هنگام حل عددی مسائل موج، باید از مقیاس های زمان و طول درگیر در مسئله آگاه بود، همانطور که در زیر مورد بحث قرار خواهد گرفت.
مقیاس های طول و زمان
هنگام حل مسائل آکوستیک، مهم است که در مورد طول و مقیاس های زمانی اصلی درگیر در سیستم فکر کنید. برخی از مقیاس ها توسط فیزیک مسئله تنظیم می شوند، در حالی که برخی دیگر با روش حل عددی تنظیم می شوند. اندازه نسبی این مقیاسها ممکن است بر دقت راهحل و همچنین انتخاب رابط فیزیک مورد استفاده برای مدلسازی مسئله تأثیر بگذارد.
هنگام کار با آکوستیک در حوزه فرکانس، یعنی حل معادله هلمهولتز، تنها یک مقیاس زمانی T وجود دارد (پریود) و با فرکانس، T = 1/f تنظیم میشود . چندین مقیاس طول وجود دارد: طول موج λ = c / f ، کوچکترین بعد هندسی Lmin ، اندازه مش h و ضخامت لایه مرزی آکوستیک δ ( این مورد در مدلهای با تلفات مورد بحث قرار میگیرد.). برای به دست آوردن یک راه حل دقیق، مش باید به اندازه کافی خوب باشد که هم ویژگی های هندسی و هم طول موج را مشخص کند. به عنوان یک قاعده کلی، حداکثر اندازه مش باید کمتر یا مساوی λ / N باشد ، که در آن N عددی بین 5 تا 10 است و به گسسته سازی فضایی بستگی دارد.
توجه داشته باشید که وقتی طول موج از مقیاس طول مشخصه در مدل کوچکتر می شود، می توان از دو رابط در هندسی آکوستیک استفاده کرد. معادلات حل شده در اینجا به محدودیت های مش یکسانی نیاز ندارند و می توانند برای مدل سازی سیستم های بسیار بزرگتر (اندازه گیری شده در طول موج) در مقایسه با حل معادله هلمهولتز استفاده شوند.
برای مشکلات صوتی گذرا همین ملاحظات اعمال می شود. با این حال، چندین مقیاس زمانی جدید نیز معرفی شده است. یکی از محتویات فرکانس سیگنال و با وضوح فرکانس حداکثر مطلوب داده می شود: T = 1 / f max . دیگری با اندازه گام زمانی Δ t استفاده شده توسط حلگر عددی داده می شود. یک شرط در شرایط به اصطلاح CFL رابطه بین اندازه گام زمانی و اندازه مش حداقل h دقیقه را دیکته می کند ، عدد Courant به صورت تعریف می شود.
(4)
که در آن c سرعت صوت در سیستم است. برای تمام رابط های گذرا موجود با ماژول آکوستیک، حل کننده به طور خودکار برای برآورده کردن این معیار تنظیم می شود. برای رابط های مبتنی بر FEM، این شرط برای دستیابی به تعادل کافی بین وضوح در زمان و مکان تفسیر می شود. کاربر فقط باید حداکثر فرکانس f max را وارد کند تا توسط مدل حل شود. برای رابطهای مبتنی بر dG-FEM، این شرط به صراحت برای دستیابی به دقت و ثبات استفاده میشود.
برای اجرای شبیهسازیهای صوتی دقیق، مهم است که در مورد این مقیاسهای فیزیکی و عددی و تأثیر آنها بر همگرایی و صحت جواب عددی فکر کنیم. یک رویکرد عملی خوب، آزمایش استحکام یک راه حل در مقایسه با تغییرات مش در همه موارد و زمان عددی گام در مسائل گذرا است. اگر مقداری از محلول، در محدوده دقت معین، با پالایش مش تغییر کند، احتمالاً مش به اندازه کافی خوب نبوده است.
شرایط مرزی
شرایط مرزی ماهیت مرزهای حوزه محاسباتی را مشخص می کند. برخی موانع فیزیکی واقعی را تعریف می کنند، مانند یک دیوار سخت صدا یا یک رابط متحرک. برخی دیگر که شرایط مرزی مصنوعی نامیده می شوند، برای کوتاه کردن دامنه استفاده می شوند. برای مثال، شرایط مرزی مصنوعی برای شبیه سازی یک مرز باز که در آن هیچ صدایی منعکس نمی شود، استفاده می شود. همچنین ممکن است یک مرز واکنش مانند یک صفحه سوراخ شده را تقلید کند.
امواج الاستیک
انتشار صوت در جامدات از طریق نوسانات الاستیک با دامنه کوچک شکل و ساختار جامدات اتفاق می افتد. این امواج الاستیک به صورت امواج صوتی معمولی به سیالات اطراف منتقل می شوند. از طریق برهم کنش آکوستیک-ساختار، فشار سیال باعث بار سیال بر روی حوزه جامد می شود و شتاب ساختاری بر دامنه سیال به عنوان یک شتاب معمولی در سراسر مرز مایع- جامد تأثیر می گذارد. این به عنوان لرزش آکوستیک نیز شناخته می شود.
ماژول آکوستیک دارای رابط Poroelastic Waves برای مدلسازی امواج poroelastic است که در مواد متخلخل منتشر میشوند. این امواج ناشی از تعامل پیچیده بین تغییرات فشار صوتی در سیال اشباع و تغییر شکل الاستیک ماتریس متخلخل جامد است.
مدل های با ضرر
برای مدلسازی دقیق آکوستیک در هندسههایی با ابعاد کوچک، لازم است اثرات هدایت حرارتی و تلفات ویسکوز به طور صریح در معادلات حاکم گنجانده شود. در نزدیکی دیوارها، ویسکوزیته و هدایت حرارتی مهم میشوند زیرا میدان صوتی لایههای مرزی چسبناک و حرارتی ایجاد میکند که تلفات قابل توجهی هستند. برای مدلسازی این پدیدهها به شرح مفصلی نیاز است. رابط اختصاصی Thermoviscous Acoustics، Frequency Domain معادلات خطی کامل Navier-Stokes، تداوم و انرژی را به طور همزمان حل می کند. رابط فیزیک فشار آکوستیک p ، بردار سرعت ذره u و تغییرات دمای آکوستیک T را حل می کند.. اینها تغییرات صوتی در بالای مقادیر میانگین پس زمینه هستند.
مقیاس طولی که در آن توصیف صوتی ترموویسکوز ضروری است با ضخامت لایههای مرزی چسبناک (v) و حرارتی (امین) ارائه میشود.
که در آن μ ویسکوزیته دینامیکی، k ضریب هدایت حرارتی، و Cp ظرفیت گرمایی ویژه در فشار ثابت است . این دو مقیاس طولی یک لایه مرزی صوتی را تعریف میکنند که باید توسط شبکه محاسباتی حل شود.
راه دیگر برای معرفی تلفات در معادلات حاکم، استفاده از مدلهای سیال معادل موجود در رابطهای آکوستیک فشار است. به روشی همگن، این ویژگیهای تضعیف را به سیال تودهای معرفی میکند که مکانیسمهای تلفات مختلف را تقلید میکند. این در تضاد با رابط های صوتی ترموویسکوز است که تلفات را به صراحت در جایی که اتفاق می افتد، یعنی در لایه مرزی آکوستیک نزدیک دیوارها، مدل می کنند. مدلهای سیال شامل تلفات ناشی از هدایت حرارتی و ویسکوزیته (در ویژگی اصلی حوزه آکوستیک فشار)، مدلهایی برای شبیهسازی میرایی در مواد متخلخل خاص (در ویژگی حوزه Poroacoustics)، و مدلهایی برای تقلید از تلفات جذب مرزی در طولانیمدت باریک است. کانال ها (ویژگی دامنه آکوستیک منطقه باریک). در صورت امکان، مدلهای سیال معادل از نظر محاسباتی بسیار کمتر از
آکوستیک هندسی
در فرکانسهای بالا، زمانی که طول موج بسیار کوچکتر از ویژگیهای هندسی مشخصه است، حل مسائل آکوستیک با استفاده از آکوستیک فشار غیرعملی است. در اینجا، روشهای دیگری مانند روشهای پرتو یا قیاسهای انتشار انرژی استفاده میشوند. این روشها به عنوان روشهای آکوستیک هندسی شناخته میشوند و برای مدلسازی آکوستیک اتاق، آکوستیک سالن کنسرت و انتشار در فضای باز در فواصل زیاد استفاده میشوند. شاخه Geometrical Acoustics شامل Ray Acoustics و Acoustic Diffusion Equation است.
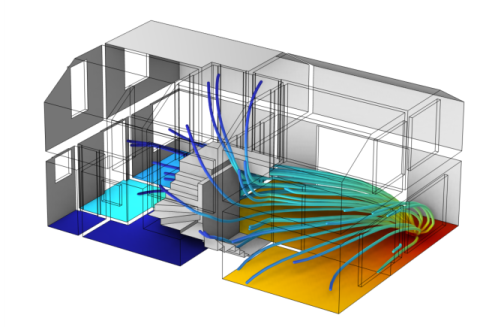
شکل 7: سطح فشار صدا و شار انرژی در داخل یک خانه دو طبقه که با استفاده از رابط فیزیک معادله انتشار صوتی مدل شده است. شکل گرفته شده از مدل آکوستیک خانه یک خانواده که در کتابخانه برنامه یافت می شود.

شکل 8: مدل ردیابی پرتو یک سالن موسیقی مجلسی شامل موقعیت اشعه در 35 میلی ثانیه. شکل گرفته شده از مدل سالن موسیقی مجلسی موجود در کتابخانه برنامه.




