معرفی
سیستم لورنز سیستمی از معادلات دیفرانسیل معمولی (معادلات لورنز) است که برای اولین بار توسط ادوارد N. Lorenz مورد مطالعه قرار گرفت. برای مقادیر پارامترهای خاص و شرایط اولیه، سیستم ODE ها راه حل های آشفته ای دارد. سپس راه حل یک جاذبه به اصطلاح عجیب به نام جاذبه لورنز است که توسط لورنز در سال 1962 کشف شد.
تعریف مدل
معادلات لورنز به عنوان یک مدل ریاضی ساده شده برای همرفت اتمسفر توسعه داده شد. آنها سیستمی از سه ODE جفت شده با سه حالت (درجات آزادی)، u ، v و w هستند :
(1)
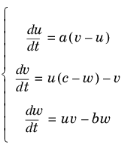
در اینجا، پارامترهای a ، b و c به طور کلی اعداد اسکالر مثبت هستند. همه راه حل ها آشفته نیستند، اما لورنز دریافت که مقادیر 10، 8/3، و 28، به ترتیب، یک سیستم لورنز با رفتار آشفته را نشان می دهند.
پارامتر | ارزش |
آ | 10 |
ب | 8/3 |
ج | 28 |
برای مقادیر پارامتر در جدول 1 ، راه حل این سیستم معادلات به یک جسم هندسی در فضای فازی که توسط مختصات راه حل ( u , v , w ) تعریف شده است نزدیک می شود که یک جاذبه عجیب یا جاذبه لورنز نامیده می شود.. می توان نشان داد که این شی از یک توپولوژی هندسی استاندارد، مانند یک دیسک (با بعد 2) یا یک خط (با بعد 1) نیست، بلکه توپولوژی عجیب دیگری با ابعاد فراکتالی بزرگتر از 2 است. علاوه بر این، تقریباً تمام اختلالات به راه حل با گذشت زمان به سرعت رشد می کند. به عنوان نمونه ای از این رفتار، مدل از یک راه حل اولیه نزدیک به جذب کننده شروع می کند و بررسی می کند که چگونه یک اختلال بسیار کوچک در این داده های اولیه رشد می کند. به طور دقیق تر، راه حل اولیه استفاده شده در اینجا ( u , v , w ) = (- 10, – 4.45, 35.1 ) است که در حالت آشفته دوم به ( u , v , w تغییر می کند.) = (- 10 + pert , − 4.45 + pert , 35.1 + pert ) که در آن pert = 10 − 11 . برای اطمینان از اینکه تفاوت بین مسائل بدون اغتشاش و اغتشاش بزرگتر از خطاهای عددی است، تلورانس های مورد استفاده در هنگام حل مدل بسیار دقیق هستند. یک ضریب تحمل مطلق پیش فرض 0.1 استفاده می شود، به این معنی که تلورانس مطلق 0.1 برابر TOL تحمل نسبی استفاده شده در مدل است.
نتایج و بحث
ابتدا خطاهای عددی را در نظر بگیرید. جدول 2 نتایج حل ( u ، v ، w ) را برای دو شبیه سازی بدون اغتشاش با TOL = 10-15 و TOL = 10-16 ، به ترتیب در زمان های t = 20 ، 25، 30 ، و 35 نشان می دهد . واضح است که برای t = 20 همه 5 رقم نمایش داده شده نتیجه موافق هستند، که نشانه ای قوی از یک راه حل بسیار دقیق است. در مقابل، در حال حاضر در t = 30 فقط دو رقم صحیح باقی مانده است. هم خطاهای عددی و هم آشفتگی ها در طول زمان رشد خواهند کرد. در نهایت هیچ رقمی با این روش و این تلرانس ها درست نمی شود.
به من | تی | تو | V | W |
10 -15 | 20 | 1.0748 | -2.9811 | 26.380 |
10 -15 | 25 | 7.9602 | 13.758 | 14.996 |
10 -15 | 30 | 3.7537 | 4.1334 | 20.640 |
10 -15 | 35 | -8.1947 | -4.9358 | 30.479 |
10 -16 | 20 | 1.0748 | -2.9811 | 26.380 |
10 -16 | 25 | 7.9595 | 13.757 | 14.994 |
10 -16 | 30 | 3.7181 | 4.1095 | 20.566 |
10 -16 | 35 | 3.5213 | 1.4743 | 24.833 |
شکل 1 نشان می دهد که چگونه تفاوت بین مشکلات بدون مزاحمت و آشفته با گذشت زمان افزایش می یابد. نمودار تفاوت مطلق بین دو راه حل را برای دقیق ترین (مقدار) مقدار تحمل به عنوان تابعی از زمان همراه با تخمینی برای میانگین نرخ رشد ارائه شده توسط e λ t نشان می دهد ، که در آن λ = 0.9، حداکثر توان لیاپانوف برای این مدلبا توجه به ادبیات توجه داشته باشید که نمودار از یک محور عمودی با مقیاس لگاریتمی استفاده می کند. همانطور که نمودار نشان می دهد، رشد اختلاف به مقدار صحیح نزدیک است تا زمانی که به O(1) برسد، پس از آن رشد چندانی ندارد. دلیل آن این است که همه راه حل ها به جذب کننده نزدیک می شوند، بنابراین تفاوت محدود می شود.
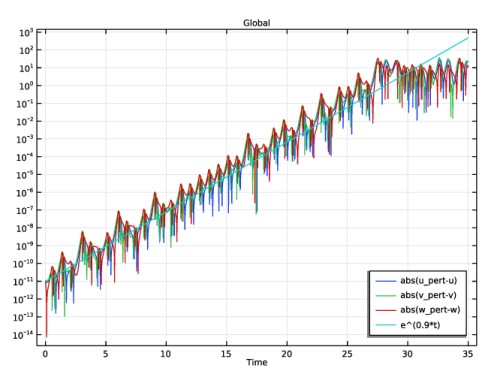
شکل 1: تفاوت بین راه حل های بدون اغتشاش و آشفته به عنوان تابعی از زمان. خط مستقیم میانگین نرخ رشد تخمین زده شده به صورت exp (λt ) را نشان می دهد که λ = 0.9 است .
با مجموعه ای از مقادیر پارامتر انتخاب شده، سیستم لورنز به عنوان یک جاذبه لورنز رفتار می کند. نمودار مسیرهای نقطه ای در شکل 2 فضای فاز، مشخصه “پروانه” یا “شکل هشت” این جاذبه را نشان می دهد.
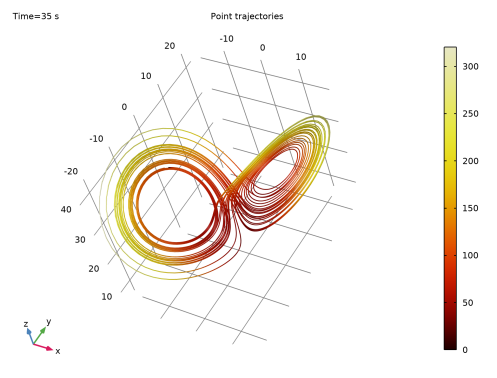
شکل 2: الگوی معمولی برای جاذب لورنز که با استفاده از نمودار مسیرهای نقطه ای از فضای فاز تجسم شده است.
نکاتی درباره پیاده سازی COMSOL
برخی از نکات کلیدی برای تنظیمات، حل، و تجسم نتایج برای جذب کننده لورنز در COMSOL Multiphysics:
• | با استفاده از رابط جهانی ODEs و DAEs، وارد کردن ODE هایی که سیستم لورنز را در معادله 1 تعریف می کنند، ساده است . |
• | برای راهحلی سریع برای مجموعهای از ODEهای جفتشده، روش صریح مرحلهبندی زمانی Dormand-Prince کارآمد است. با تنظیم تلرانس نسبی، می توانید دقت محلول را کنترل کنید. |
• | عملگر withsol() و Global Plot برای تولید نمودار در شکل 1 استفاده شده است . |
• | نمودار مسیرهای نقطه ای در فضای فاز برای حالت ها، الگوی معمولی “پروانه” یا “شکل هشت” را نشان می دهد که در شکل 2 نشان داده شده است . |
ارجاع
1. http://en.wikipedia.org/wiki/Lorenz_system
مسیر کتابخانه برنامه: COMSOL_Multiphysics/Equation_Based/lorenz_attractor
دستورالعمل مدلسازی
از منوی File ، New را انتخاب کنید .
جدید
در پنجره جدید ، روی  Model Wizard کلیک کنید .
Model Wizard کلیک کنید .
مدل جادوگر
1 | در پنجره Model Wizard ، روی |
2 | در درخت Select Physics ، Mathematics>ODE و DAE Interfaces>Global ODEs and DAEs (ge) را انتخاب کنید . |
3 | روی افزودن کلیک کنید . |
4 |
5 | در درخت انتخاب مطالعه ، General Studies>Time Dependent را انتخاب کنید . |
6 |
ریشه
ODE های اینجا بدون بعد هستند، بنابراین از هیچ سیستم واحدی استفاده نکنید.
1 | در پنجره Model Builder ، روی گره ریشه کلیک کنید. |
2 | در پنجره تنظیمات گره ریشه ، بخش Unit System را پیدا کنید . |
3 | از لیست سیستم واحد ، هیچکدام را انتخاب کنید . |
تعاریف جهانی
پارامترهای a ، b و c پارامترهای سیستمی برای سیستم لورنز ODE ها هستند. مقادیر پیش فرض 10، 8/3 و 28 به ترتیب مقادیری هستند که لورنز استفاده کرده است.
پارامترهای 1
1 | در پنجره Model Builder ، در قسمت Global Definitions روی Parameters 1 کلیک کنید . |
2 | در پنجره تنظیمات برای پارامترها ، بخش پارامترها را پیدا کنید . |
3 | در جدول تنظیمات زیر را وارد کنید: |
نام | اصطلاح | ارزش | شرح |
آ | 10 | 10 | پارامتر سیستم |
ب | 8/3 | 2.6667 | پارامتر سیستم |
ج | 28 | 28 | پارامتر سیستم |
پرت | 0 | 0 | اختلال داده های اولیه |
به من | 1e-6 | 1E-6 | تحمل حل کننده |
فینال | 35 | 35 | زمان پایان برای شبیه سازی |
ODE و DAE جهانی (GE)
از یک رابط جهانی ODEs و DAEs برای وارد کردن سه ODE که یک سیستم Lorenz را تعریف می کنند، استفاده کنید. داده های اولیه را نزدیک به جاذبه عجیب انتخاب کنید تا حساسیت آن را مطالعه کنید. اغتشاش به همه اجزاء اضافه می شود.
معادلات جهانی 1
1 | در پنجره Model Builder ، در قسمت Component 1 (comp1)>Global ODEs and DAEs (ge) روی معادلات جهانی 1 کلیک کنید . |
2 | در پنجره تنظیمات برای معادلات جهانی ، بخش معادلات جهانی را پیدا کنید . |
3 | در جدول تنظیمات زیر را وارد کنید: |
نام | F(U,UT,UTT,T) | مقدار اولیه (U_0) | مقدار اولیه (U_T0) |
تو | ut-a*(vu) | -10+پرت | 0 |
v | vt-c*u+v+u*w | -4.45+ pert | 0 |
w | wt-u*v+b*w | 35.1+ درصد | 0 |
مطالعه 1
برای یک راه حل دقیق، از روش صریح Dormand-Prince 5 time-stapping استفاده کنید. تلورانس برای این روش به طور سیستماتیک تغییر خواهد کرد.
راه حل 1 (sol1)
در نوار ابزار مطالعه ، روی  Show Default Solver کلیک کنید .
Show Default Solver کلیک کنید .
مرحله 1: وابسته به زمان
1 | در پنجره Model Builder ، در بخش مطالعه 1 ، روی Step 1: Time Dependent کلیک کنید . |
2 | در پنجره تنظیمات مربوط به زمان وابسته ، قسمت تنظیمات مطالعه را پیدا کنید . |
3 |
4 | در کادر محاورهای Range ، 0.01 را در قسمت متن Step تایپ کنید . |
5 | در قسمت متن Stop ، Tfinal را تایپ کنید . |
6 | روی Replace کلیک کنید . |
7 | در پنجره تنظیمات مربوط به زمان وابسته ، قسمت تنظیمات مطالعه را پیدا کنید . |
8 | از لیست Tolerance ، User controlled را انتخاب کنید . |
9 | در قسمت متنی Relative tolerance ، TOL را تایپ کنید . |
راه حل 1 (sol1)
1 | در پنجره Model Builder ، گره Study 1>Solver Configurations>Solution 1 (sol1) را گسترش دهید ، سپس روی Time-Dependent Solver 1 کلیک کنید . |
2 | در پنجره تنظیمات برای حل وابسته به زمان ، برای گسترش بخش Time Steping کلیک کنید . |
3 | از لیست نوع Solver ، Explicit را انتخاب کنید . |
4 | از لیست روش ، Runge – Kutta را انتخاب کنید . |
5 | از لیست روش Runge – Kutta ، Dormand – Prince 5 را انتخاب کنید . |
6 | در پنجره Model Builder ، گره Study 1>Solver Configurations>Solution 1 (sol1)>Time-Dependent Solver 1 را گسترش دهید ، سپس روی Direct کلیک کنید . |
7 | در پنجره تنظیمات برای Direct ، بخش عمومی را بیابید . |
8 | از لیست حل ، PARDISO را انتخاب کنید . |
این حل کننده برای مسائل کوچک با تعداد مراحل زمانی زیاد کارآمدتر است.
جارو پارامتریک
از یک Sweep پارامتریک برای مطالعه اثر یک اغتشاش کوچک بر داده های اولیه و تغییرات در یک تحمل حل کننده بسیار دقیق استفاده کنید.
1 | در نوار ابزار مطالعه ، روی |
2 | در پنجره تنظیمات برای جابجایی پارامتری ، بخش تنظیمات مطالعه را پیدا کنید . |
3 |
4 | در جدول تنظیمات زیر را وارد کنید: |
نام پارامتر | لیست مقادیر پارامتر |
pert (اغتشاش داده های اولیه) | 1e-11 0 |
TOL (تحمل حل کننده) | 1e-15 1e-16 |
5 | از لیست نوع Sweep ، همه ترکیبات را انتخاب کنید . |
6 | در نوار ابزار مطالعه ، |
نتایج
گروه طرح 1 بعدی 1
از یک نمودار جهانی برای تجسم نحوه تغییر راه حل به دلیل اغتشاش کوچک استفاده کنید و یک رشد نمایی مطابق با بزرگترین توان لیاپانوف 0.9 که در ادبیات گزارش شده برای مقایسه اضافه کنید. توجه داشته باشید که چگونه رشد متوقف می شود زمانی که انحراف از O (1) است. این توسط اثر جاذبه ایجاد می شود. انحرافات نمی توانند بزرگتر باشند، زیرا همه راه حل ها به جذب کننده نزدیک هستند.
1 | در پنجره Settings for 1D Plot Group ، بخش Data را پیدا کنید . |
2 | از لیست انتخاب پارامتر (pert) ، از لیست را انتخاب کنید . |
3 | در لیست مقادیر پارامتر (pert) ، 1E-11 را انتخاب کنید . |
4 | از لیست انتخاب پارامتر (TOL) ، از لیست را انتخاب کنید . |
5 | در لیست مقادیر پارامتر (TOL) ، 1E-16 را انتخاب کنید . |
جهانی 1
1 | در پنجره Model Builder ، گره 1D Plot Group 1 را گسترش دهید ، سپس روی Global 1 کلیک کنید . |
2 | در پنجره تنظیمات برای جهانی ، بخش y-Axis Data را پیدا کنید . |
3 | در جدول تنظیمات زیر را وارد کنید: |
اصطلاح | شرح |
abs(u-withsol(‘sol2’,u,setval(pert,0),setval(TOL,TOL), setval(t,t))) | abs(u_pert-u) |
abs(v-withsol(‘sol2’,v,setval(pert,0),setval(TOL,TOL), setval(t,t))) | abs(v_pert-v) |
abs(w-withsol(‘sol2’,w,setval(pert,0),setval(TOL,TOL), setval(t,t))) | abs (w_pert-w) |
pert*exp(0.9*t) | e^(0.9*t) |
4 | برای گسترش بخش Legends کلیک کنید . از فهرست Legends ، Manual را انتخاب کنید . |
5 | در جدول تنظیمات زیر را وارد کنید: |
افسانه ها |
abs(u_pert-u) |
abs(v_pert-v) |
abs (w_pert-w) |
e^(0.9*t) |
6 | قسمت x-Axis Data را پیدا کنید . از فهرست داده های منبع محور ، زمان را انتخاب کنید . |
گروه طرح 1 بعدی 1
1 | در پنجره Model Builder ، روی 1D Plot Group 1 کلیک کنید . |
2 | در نوار ابزار 1D Plot Group 1 ، روی |
3 |
4 | در پنجره تنظیمات برای گروه طرح 1 بعدی ، قسمت Legend را پیدا کنید . |
5 | از لیست موقعیت ، پایین سمت راست را انتخاب کنید . |
با نمودار در شکل 1 مقایسه کنید .
از نمودار مسیرهای نقطه ای برای تجسم راه حل سیستم لورنز به عنوان مسیرهای نقطه ای همانطور که در شکل 2 نشان داده شده است استفاده کنید .
گروه طرح سه بعدی 2
در نوار ابزار صفحه اصلی ، روی  Add Plot Group کلیک کنید و 3D Plot Group را انتخاب کنید .
Add Plot Group کلیک کنید و 3D Plot Group را انتخاب کنید .
مسیرهای نقطه 1
1 | در نوار ابزار 3D Plot Group 2 ، روی |
2 | در پنجره تنظیمات برای مسیرهای نقطه ، بخش Trajectory Data را پیدا کنید . |
3 | در قسمت متن X-expression ، u را تایپ کنید . |
4 | در قسمت متن Y-expression ، v را تایپ کنید . |
5 | در قسمت متن بیان Z ، w را تایپ کنید . |
6 | قسمت Coloring and Style را پیدا کنید . زیربخش Line style را پیدا کنید . از لیست نوع ، لوله را انتخاب کنید . |
7 | چک باکس Radius scale factor را انتخاب کنید . در قسمت متن مرتبط، 0.1 را تایپ کنید . |
بیان رنگ 1
1 | روی Point Trajectories 1 کلیک راست کرده و Color Expression را انتخاب کنید . |
2 | در پنجره تنظیمات برای بیان رنگ ، قسمت Coloring and Style را پیدا کنید . |
3 |
4 | در کادر محاوره ای Color Table ، Thermal>ThermalDark را در درخت انتخاب کنید. |
5 | روی OK کلیک کنید . |
6 | در پنجره تنظیمات برای Color Expression ، بخش Expression را پیدا کنید . |
7 | در قسمت متن Expression ، sqrt(ut^2+vt^2+wt^2) را تایپ کنید . |
8 | در نوار ابزار 3D Plot Group 2 ، روی |
با کلیک بر روی پنجره گرافیک و کشیدن می توانید جاذبه را از دیدگاه های مختلف کشف کنید.
مراحل زیر یک انیمیشن از جاذبه لورنز ایجاد می کند.
انیمیشن 1
1 | در نوار ابزار نتایج ، روی |
2 | در پنجره تنظیمات برای انیمیشن ، روی |
3 | قسمت Scene را پیدا کنید . از لیست موضوع ، 3D Plot Group 2 را انتخاب کنید . |
4 | قسمت Frames را پیدا کنید . در قسمت متنی Number of frames عدد 200 را تایپ کنید . |
5 |
سپس، راه حل بدون اغتشاش را در زمان های انتخابی ارزیابی کنید و با مقایسه مقادیر دو تلورانس مورد استفاده، میزان دقت آن را مطالعه کنید. توجه داشته باشید که چگونه چندین رقم برای مقادیر زمانی متوسط یکسان هستند، در حالی که هیچ رقمی در زمان نهایی یکسان نیست.
متغیرهای حالت
1 | در پنجره Model Builder ، گره Results>Derived Values را گسترش دهید ، سپس روی Global Evaluation 1 کلیک کنید . |
2 | در پنجره تنظیمات برای ارزیابی جهانی ، بخش داده را پیدا کنید . |
3 | از لیست انتخاب پارامتر (pert) ، از لیست را انتخاب کنید . |
4 | در لیست مقادیر پارامتر (pert) ، 0 را انتخاب کنید . |
5 | از لیست انتخاب زمان ، Interpolated را انتخاب کنید . |
6 | در قسمت نوشتاری Times (s) ، 20،25،30،35 را تایپ کنید . |
7 |
نتایج باید با نتایج نمایش داده شده در جدول 2 مطابقت داشته باشد .
8 | در قسمت نوشتار Label ، متغیرهای State را تایپ کنید . |




