برای اختصار، معادله 1 بعدی 2-58 را در نظر بگیرید . به منظور استخراج فرمول PML در حوزه زمان، مراحل زیر انجام می شود ( مراجعه 39 ). ابتدا شکل خاصی از معادله نگاشت 2-57 را در نظر بگیرید :
(2-59)  ،
،
که بازده  .
.
سپس، با در نظر گرفتن رابطه 2-59 ، معادله 2-58 را در 1+ σ( x )/ i ω ضرب کنید . معادله 2-58 به شکل زیر تبدیل می شود:
(2-60)  .
.
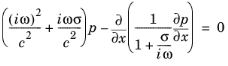 .
.تبدیل به حوزه زمان طبق قانون انجام می شود  . کاربرد مستقیم آن در معادله 2-60 منجر به انتگرال زمانی p می شود . برای جلوگیری از این امر، یک متغیر کمکی u معرفی شده است:
. کاربرد مستقیم آن در معادله 2-60 منجر به انتگرال زمانی p می شود . برای جلوگیری از این امر، یک متغیر کمکی u معرفی شده است:
(2-61)  .
.
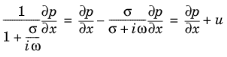 .
.معادله 2-60 و معادله 2-61 سیستمی از معادلات دیفرانسیل جزئی در حوزه زمانی معادل حوزه فرکانس معادله 2-58 به دست می دهد :
(2-62)
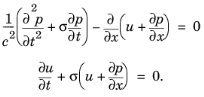
اشتقاق مدل در فضای سه بعدی، که در آن به متغیرهای کمکی بیشتری نیاز است، در Ref آورده شده است. 39 .
در موارد متقارن محوری، کشش مختصات در حوزههای PML در مختصات منحنی بیان میشود. یک مطالعه کامل از استفاده از PML برای چنین مشکلاتی در حوزه های فرکانس و زمان در Ref آورده شده است. 40 .




