در زیر الگوریتم مورد استفاده برای محاسبه شدت پرتو هنگامی که Intensity computation روی Compute intensity یا Compute intensity and power در بخش محاسبه شدت واسط فیزیک تنظیم شده است را توضیح می دهد. در این الگوریتم، هر پرتو به‌عنوان یک جبهه موج منتشر شده در نظر گرفته می‌شود که یک زاویه جامد کوچک را تحت تأثیر قرار می‌دهد. الگوریتم تنها زمانی معتبر است که پرتوها در محیط های همگن منتشر شوند. متغیرهای وابسته کمکی زیر برای هر پرتو تعریف شده است:
به صورت سه بعدی:
• | شدت پرتو اولیه I 0 که در ناپیوستگی‌ها و دیواره‌های مواد مجدداً مقداردهی می‌شود. |
• | انتگرال A ضریب تضعیف در طول مسیر پرتو. |
• | دو شعاع اولیه انحنای، r 1 ، i و r 2 ، i . |
• | دو شعاع انحنای اصلی r 1 و r 2 که نشان دهنده حداکثر و حداقل شعاع انحنای تقاطع جبهه موج با یک صفحه دلخواه است. |
• | سه جزء بردار واحد e 1 در جهت مربوط به اولین شعاع اصلی انحنا. این اطلاعات برای شروع مجدد شعاع اصلی انحنا در مرزهای منحنی استفاده می شود. |
به صورت دو بعدی:
• | شدت پرتو اولیه I 0 . |
• | انتگرال A ضریب تضعیف در طول مسیر پرتو. |
• | یک شعاع اصلی اولیه انحنا، r 1 ، i . |
• | یک شعاع انحنای r 1 جبهه موج. فرض بر این است که همه جبهه‌های موج امواج استوانه‌ای همگرا یا واگرا هستند، بنابراین نیازی به تعریف شعاع دوم انحنا نیست. |
اگر محاسبات Intensity روی Compute Intensity در رسانه های درجه بندی شده یا Compute Intensity and Power در رسانه های درجه بندی شده تنظیم شده باشد، از الگوریتم متفاوتی برای محاسبه شدت هر پرتو استفاده می شود . این الگوریتم تأثیر رسانه های درجه بندی شده بر شدت پرتو را محاسبه می کند، اما همچنین برای محیط های همگن کندتر و دقیق تر است. متغیرهای وابسته کمکی زیر برای هر پرتو تعریف شده است:
به صورت سه بعدی:
• | متغیر کمکی شدت Γ . |
• | انتگرال A ضریب تضعیف در طول مسیر پرتو. |
• | دو محاسبه انحنای اصلی به متغیرهای α 1 و α 2 و زاویه چرخش کمک می کند  که جهت گیری جهات انحنای اصلی را نشان می دهد. یک متغیر کمک اضافی به صورت داخلی برای شناسایی قطب ها در تعریف سیستم مختصات محلی و برای تعریف مجدد سیستم مختصات محلی بر این اساس استفاده می شود. |
به صورت دو بعدی:
• | متغیر کمکی شدت Γ . |
• | انتگرال A ضریب تضعیف در طول مسیر پرتو. |
• | یک محاسبه انحنای اصلی به متغیر α 1 کمک می کند . |
برای گزینه های Compute Power ، Compute Intensity and Power و Compute Intensity and Power در رسانه های درجه بندی شده، یک متغیر وابسته کمکی اضافی برای نشان دادن کل توان ارسال شده توسط هر پرتو تعریف شده است. مانند شدت، قدرت نیز تحت تأثیر رسانه های جذب کننده و بازتاب یا شکست در مرزها قرار می گیرد. بر خلاف شدت، قدرت به دلیل تمرکز یا واگرایی یک بسته پرتو تغییر نمی کند.
شعاع اصلی انحنا
در مدل‌های سه‌بعدی، هر پرتو به‌عنوان یک جبهه موج در نظر گرفته می‌شود که دو شعاع اصلی انحنای r1 و r2 برای آن تعریف شده‌اند. علاوه بر این، مقادیر دو شعاع اصلی انحنا به صورت r 1,i و r2 ,i هر زمان که پرتو به یک مرز برسد ذخیره می شود.
در حوزه ها، معادلات
حل می شوند. شعاع انحنای منفی نشان می دهد که جبهه موج با انتشار پرتو در حال گسترش است، در حالی که شعاع انحنای مثبت نشان می دهد که جبهه موج در حال همگرایی است. مکان پیوسته ای از نقاط که در آن هر یک از شعاع های اصلی انحنا برابر با صفر است، سطح سوزاننده نامیده می شود. بردار واحد e 1 طوری تعریف می شود که r 1 شعاع انحنای تقاطع جبهه موج با صفحه مماس بر e 1 و بردار موج k باشد . به طور مشابه، اگر بردار e 2 به گونه ای تعریف شود که
سپس r 2 شعاع انحنای تقاطع جبهه موج با صفحه مماس بر e 2 و k است . اجزای e 1 به عنوان متغیرهای وابسته کمکی برای هر پرتو ذخیره می شوند. سپس اجزای e 2 را می توان در هر زمان از e 1 و k مشتق کرد .
شعاع های اصلی انحنا در ناپیوستگی های مواد اولیه مجدداً شروع می شوند و جهت بردارهای واحد e1 و e2 ممکن است تغییر کند. اگر بردار واحد در جهت پرتو فرودی n i با سطح نرمال n s موازی نباشد ، می توان یک صفحه مماس منحصر به فرد به نام صفحه تابش تعریف کرد که شامل پرتوهای تابیده، منعکس شده و شکست شده است. . بردار واحد نرمال برای این صفحه، u 0 ، به صورت تعریف می شود
اگر پرتو با سطح نرمال باشد، آنگاه پرتو فرودی موازی با پرتو شکسته و ضد موازی با پرتو بازتاب شده است، و u 0 می تواند هر بردار واحد دلخواه متعامد بر n i باشد . علاوه بر بردار واحد نرمال با صفحه تابش، بردارهای واحد زیر مماس بر جبهه موج فرودی، جبهه موج شکسته، جبهه موج بازتابی و نرمال سطح تعریف می شوند:
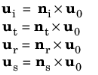
که در آن زیرنویس‌های i ، t و r به ترتیب نشان‌دهنده جبهه‌های موج حادثه، شکست و انعکاس هستند. برای جبهه موجی که در جهت n منتشر می شود ، با انحناهای اصلی k 1 = 1 / r 1 و k 2 = 1 / r 2 که به ترتیب برای جهات e 1 و e 2 تعریف شده اند ، انحناهای اصلی در دو جهت متعامد دیگر e 1 ‘ و e 2 ‘ (هر دو متعامد بهn ) هستند
(8-1)
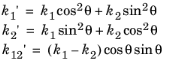
که در آن θ زاویه چرخش حول n است که بردارهای e 1 و e 2 را به ترتیب به e 1 ‘ و e 2 ‘ تبدیل می کند . از آنجایی که k 1 ‘ و k 2 ‘ انحنای اصلی نیستند، لازم است عناصر خارج از مورب تانسور انحنای جبهه موج برابر با k 12 ‘ درج شود .
الگوریتم زیر برای شروع مجدد شعاع اصلی انحنای جبهه موج و جهت گیری آنها استفاده می شود. شروع مجدد متغیرهای انحنا از روش Stavroudis در Ref. 2 .
1 | با توجه به n i و n s ، بردارهای واحد را در جهت پرتوهای بازتابی و شکسته، n r و n t محاسبه کنید . |
2 | بردارهای u 0 , u i , u t , u r و u s را محاسبه کنید . |
3 | زاویه چرخش θ ( i ) مورد نیاز برای تبدیل سیستم مختصات محلی با محورهای موازی با e 1 , e 2 , و n i را به یک سیستم مختصات محلی با محورهای موازی با u 0 , u i , و n i محاسبه کنید . (توجه: از بالانویس ( i ) برای تشخیص زاویه چرخش سیستم مختصات از زاویه تابش پرتو استفاده می شود که اغلب با θ i نشان داده می شود .) |
4 | انحناهای اصلی را به سیستم مختصات محلی تعریف شده توسط u 0 , u i , و n i با استفاده از رابطه 8-1 تبدیل کنید و θ ( i ) را جایگزین θ . |
5 | با توجه به دو انحنای اصلی سطح، k 1,s و k 2,s با جهات e 1,s و e 2,s , متغیرهای انحنا را به یک سیستم مختصات محلی با محورهای موازی با u 0 , u s و n s _ اجازه دهید متغیرهای انحنای جدید با k 1, s ‘ , k 2, s ‘ و k 12,s ‘ نشان داده شوند . |
6 | انحناهای جبهه موج و سطح اکنون در سیستم‌های مختصاتی تعریف شده‌اند که محور u 0 را به اشتراک می‌گذارند و تنها با یک چرخش با زاویه تابش θi در مورد u 0 تفاوت دارند . با تعریف متغیرهای η و γ در نظریه ناپیوستگی مواد ، متغیرهای انحنای پرتو شکسته را در یک سیستم مختصاتی که توسط u 0 ، u t و n t تعریف شده است با استفاده از معادلات محاسبه کنید. |
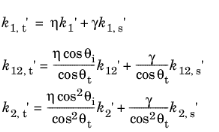
7 | انحناهای اصلی پرتو شکست را با چرخاندن سیستم مختصات تعریف شده توسط u 0 , u t و n t با زاویه θ ( t ) در حدود n t بدست آورید . زاویه θ ( t ) به صورت تعریف می شود |
8 | انحناهای اصلی پرتو شکست را دوباره شروع کنید: |
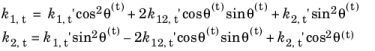
9 | انحناهای اصلی را معکوس کنید تا شعاع اصلی انحنای پرتو شکسته را بدست آورید. u 0 را در حدود n t با زاویه θ ( t ) بچرخانید تا جهت انحنای اصلی اولیه e 1,t را بدست آورید . |
10 | اگر یک پرتو منعکس شده آزاد شد، متغیرهای انحنای پرتو بازتاب شده را در یک سیستم مختصاتی که توسط u 0 ، u r و n r تعریف شده است با استفاده از معادلات محاسبه کنید. |
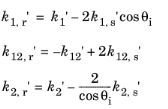
11 | انحناهای اصلی پرتو منعکس شده را با چرخاندن سیستم مختصات تعریف شده توسط u 0 , u r و n r با زاویه θ ( r ) در حدود n r بدست آورید . زاویه θ ( r ) به صورت تعریف می شود |
12 | انحناهای اصلی پرتو منعکس شده را راه اندازی کنید: |
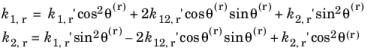
13 | انحناهای اصلی را معکوس کنید تا شعاع اصلی انحنای پرتو بازتاب شده را بدست آورید. u 0 را در حدود n r با زاویه θ ( r ) بچرخانید تا جهت اولیه انحنای اولیه e 1,r را بدست آورید . |
در اجزای دو بعدی، تنها یک شعاع اصلی انحنا محاسبه می شود. هر پرتو به عنوان یک موج استوانه ای در نظر گرفته می شود. علاوه بر این، هیچ درجه آزادی کمکی برای جهت انحنای اصلی مورد نیاز نیست، زیرا جهت خارج از صفحه همیشه می تواند به عنوان یکی از محورهای سیستم مختصات محلی که جهت جبهه موج را مشخص می کند، در نظر گرفت.
در مولفه‌های مدل متقارن محوری دوبعدی، شعاع انحنا برای جهت درون صفحه (یعنی صفحه rz ) و همچنین جهت‌های خارج از صفحه یا زاویه‌ای محاسبه می‌شود. در طول برهمکنش‌های مرزی پرتو، این شعاع‌های انحنا مجدداً شروع می‌شوند به‌گونه‌ای که گویی پرتو با یک سطح چرخشی سه‌بعدی تعامل دارد، که ممکن است شعاع‌های انحنای محدودی در هر دو جهت درون صفحه و خارج از صفحه داشته باشد.
محاسبه شدت
مقدار شدت پرتو به عنوان متغیر وابسته کمکی I 0 هنگام رها شدن یک پرتو ذخیره می شود. در هر نقطه از مسیر پرتو، شدت برابر است با
در 2 بعدی، دومین شعاع اصلی انحنای r 2 به عنوان یک فاصله دلخواه بزرگ در نظر گرفته می شود که برای هر پرتو ثابت می ماند.
