این مثال با مهربانی توسط پروفسور Simonetta Filippi و دکتر Christian Cherubini از پردیس Biomedico دانشگاه رم، ایتالیا ارائه شده است.
معرفی
مدل سازی فعالیت الکتریکی در بافت قلب گام مهمی در درک الگوهای انقباضات و اتساع قلب است. قلب پالس های الکتریکی ریتمیک تولید می کند که از نقطه ای به نام گره سینوسی شروع می شود. پالس های الکتریکی به نوبه خود باعث انقباضات مکانیکی عضله می شوند. در یک قلب سالم، این پالسهای الکتریکی از بین میروند، اما تعدادی از بیماریهای قلبی با افزایش خطر ورود مجدد سیگنالها همراه است. این بدان معنی است که نبض ثابت طبیعی مختل می شود، یک وضعیت شدید و حاد که اغلب به عنوان آریتمی شناخته می شود.
در این مثال، جنبههای مختلف انتشار سیگنال الکتریکی در بافت قلب با استفاده از معادلات فیتز هیو-ناگومو و معادلات گینزبورگ-لاندو مورد مطالعه قرار گرفتهاند که هر دو بر اساس یک هندسه حل شدهاند. الگوهای جالبی که از این نوع مدلها پدید میآیند، برای مثال، امواج مارپیچی هستند که در زمینه سیگنالهای الکتریکی قلبی، میتوانند اثراتی مشابه آنچه در آریتمی قلبی مشاهده میشود ایجاد کنند.
رسانه های هیجان انگیز و معادلات فیتز هیو-ناگومو
نشان داده شده است که بسیاری از ویژگی های مهم انتشار سیگنال الکتریکی در بافت قلب را می توان با کلاسی از معادلات که محیط های تحریک پذیر را توصیف می کند ، یعنی موادی متشکل از بخش های اولیه یا سلول هایی با ویژگی های اساسی زیر بازتولید کرد:
• | حالت استراحت کاملاً تعریف شده |
• | آستانه برای تحریک |
• | یک جفت از نوع انتشار به نزدیکترین همسایگانش |
رسانه تحریک پذیر یک مفهوم نسبتاً کلی است که برای مدل سازی تعدادی از پدیده های مختلف از جمله پالس های عصبی، گسترش آتش سوزی جنگل ها و انواع خاصی از واکنش های شیمیایی، علاوه بر سیگنال های الکتریکی در بافت قلب مفید است. یکی از مهمترین ویژگیهای کیفی که توسط رسانههای تحریکپذیر نشان داده میشود، و به همان اندازه مخرج مشترک بین تنوع پدیدههای ذکر شده در بالا، میرایی تقریباً فوری سیگنالها در زیر یک آستانه معین است. از سوی دیگر، سیگنال های بیش از این آستانه بدون میرایی منتشر می شوند.
قلب با عبور جریان یونی در داخل عضله کار می کند، بنابراین انقباضات ریتمیکی را که خون را به داخل و خارج پمپاژ می کند، تحریک می کند. یون ها از طریق منافذ یا دروازه های کوچک در غشای سلولی حرکت می کنند که می تواند باز (حالت تحریک) یا بسته (حالت استراحت) باشد.
در سلولهای عصبی و سلولهای قلبی، سه ویژگی انتزاعی رسانههای تحریکپذیر بهصورت زیر آشکار میشوند:
• | استراحت پتانسیل غشای سلولی |
• | آستانه باز کردن دروازه های یونی در غشای سلولی |
• | انتشار پراکنده سیگنال های الکتریکی |
وضعیت دروازه های غشایی در مقیاس میکروسکوپی تصادفی است، اما احتمال یک حالت داده شده را می توان به عنوان تابع پیوسته ولتاژ مدل کرد، بنابراین یک توصیف پیوسته ماکروسکوپی متوسط جریان جریان را امکان پذیر می کند.
معادلات FitzHugh-Nagumo برای محیط های تحریک پذیر ساده ترین مدل فیزیولوژیکی را با دو متغیر، یک فعال کننده و یک بازدارنده، توصیف می کند . در این مدلهای قلب، متغیر فعالکننده با پتانسیل الکتریکی مطابقت دارد، و بازدارنده متغیری است که احتمال باز بودن منافذ غشاء و آماده برای انتقال جریان یونی وابسته به ولتاژ را توصیف میکند.
دینامیک هرج و مرج و معادلات گینزبورگ-لاندو
معادلات گینزبورگ -لانداو یک روش نسبتاً ساده برای مدلسازی برخی از جنبههای انتقال ارائه میکند که توسط بسیاری از سیستمهای دینامیکی تحت تأثیر محرکهای خارجی قوی، از رفتار نوسانی دورهای به حالت آشفته با افزایش تدریجی دامنه نوسانات و کاهش تناوب نمایش داده میشود.
اگرچه اولین استفاده از آنها برای توصیف نظریه ابررسانایی بود، اما معادلات گینزبورگ-لاندو نیز ماهیت خود را عمومی میکنند (مانند معادلات فیتز هیو-ناگومو)، و نمونههایی از سیستمهای دینامیکی که میتوانید با استفاده از این معادلات با موفقیت مدلسازی کنید عبارتند از:
• | تشکیل گرداب ها در پشت یک مانع باریک در جریان سیال عرضی |
• | واکنش های شیمیایی نوسانی از نوع بلوسوف-ژابوتینسکی |
در این مثال، معادلات گینزبورگ-لانداو دینامیک امواج مارپیچی را در محیط های تحریک پذیر شبیه سازی می کند.
تعریف مدل
هندسه در اینجا یک مدل سه بعدی ساده شده از یک قلب با دو حفره است که با حفره های نیمه کروی نشان داده شده است 1 .

شکل 1: هندسه مدل.
معادلات فیتز هیو-ناگومو
معادلات به شرح زیر است:
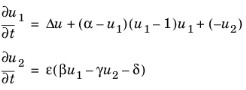
در اینجا u 1 یک پتانسیل عمل (متغیر فعال کننده) و u 2 یک متغیر دروازه (متغیر بازدارنده) است. پارامتر α نشان دهنده آستانه تحریک، ε نشان دهنده تحریک پذیری و β ، γ و δ پارامترهایی هستند که بر حالت استراحت و دینامیک سیستم تأثیر می گذارند.
شرایط مرزی برای u 1 عایق هستند، با این فرض که هیچ جریانی به داخل یا خارج از قلب جریان ندارد. شرایط اولیه توزیع پتانسیل اولیه u 1 را تعریف می کند که در آن یک ربع قلب در یک پتانسیل ثابت و بالا V 0 است ، در حالی که بقیه در صفر باقی می ماند. در عوض، ربع مجاور مقدار بالایی ν 0 برای بازدارنده u2 دارد . پیاده سازی این توزیع اولیه با استفاده از عبارات منطقی زیر راحت است، جایی که TRUE به 1 و FALSE به 0 ارزیابی می شود:
در اینجا d برابر با 10-5 است ، و در عبارات گنجانده شده است تا پتانسیل بالا را کمی از محورهای اصلی جابجا کند .
معادلات گینزبورگ-لاندو
معادلات گینزبورگ-لاندو عبارتند از:
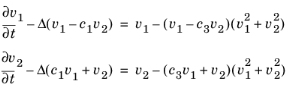
دو متغیر v 1 و v 2 به ترتیب فعال کننده و بازدارنده هستند. ثابت های c 1 و c 3 پارامترهایی هستند که خواص ماده را منعکس می کنند. این ثابت ها وجود و ماهیت راه حل های پایدار را نیز تعیین می کنند.
مانند مدل قبلی، شرایط مرزی عایق نگه داشته می شوند. شرایط اولیه، که یک گام انتقال صاف نزدیک z = 0 می دهد ، به شرح زیر است:
نکاتی درباره پیاده سازی COMSOL
ایجاد هندسه ساده شده با استفاده از ابزارهای ترسیم در COMSOL Multiphysics کاملاً ساده است. معادلات FitzHugh-Nagumo و Ginzburg-Landau نیز به راحتی در یکی از رابط های PDE وارد می شوند .
ذکر این نکته ضروری است که این معادلات به شدت غیرخطی هستند. بنابراین لازم است (مخصوصاً در مدلهای سه بعدی کامل مانند اینها) از شبکه بسیار ظریفتری استفاده شود یا از ترتیب عناصر بالاتر نسبت به این مثال استفاده شود تا نتایج با درجهای از قابلیت اطمینان برای فواصل زمانی مورد علاقه به دست آید. این امر به ویژه در حل معادلات گینزبورگ-لاندو، که پدیده های ذاتاً آشفته را توصیف می کند، مهم است. آنها به اختلالات در مقدار اولیه و به طور مشابه به خطاهای عددی در طول حل وابسته به زمان بسیار حساس هستند. ما استفاده از عنصر Hermite مرتبه چهارم را برای معادله Ginzburg-Landau توصیه می کنیم.
به دلایل بالا، نتایج ارائه شده در اینجا فقط به عنوان اولین تخمین تقریبی از رفتار کیفی در نظر گرفته شده است که می توانید انتظار داشته باشید که سیستم تحت یک محرک مشخص نشان دهد. در نتیجه، عناصر مرتبه بالاتر، مش بندی دقیق تر، و تلورانس های وابسته به زمان نسبی و مطلق کوچکتر به وضوح نتایج شبیه سازی کمی درست تری ارائه می دهند. اجرای این پیشرفت ها منجر به زمان محاسباتی طولانی تری نسبت به مدل تقریبی که در اینجا توضیح داده شده است، می شود که محاسبه آن بر روی یک کامپیوتر استاندارد چند دقیقه طول می کشد. هنگام تلاش برای این نوع مدلهای بزرگ، استفاده از پلتفرمهای 64 بیتی را قویاً توصیه میکنیم.
برای جلوگیری از هشدار در مورد واحدهای ناسازگار، پشتیبانی واحد را خاموش کنید.
نتایج و بحث
معادلات فیتز هیو-ناگومو
نمودارهای شکل 2 زیر پتانسیل عمل u 1 را نشان می دهند . برای تجسم محلول در داخل، یک چهارم پوسته بیرونی قلب و یکی از سطوح محفظه در طرح سرکوب می شود.
پارامترهای مورد استفاده در مدل همراه با پالس اولیه منجر به یک موج بازگشتی می شود که بدون میرایی در یک الگوی مارپیچی مشخص در اطراف بافت حرکت می کند.
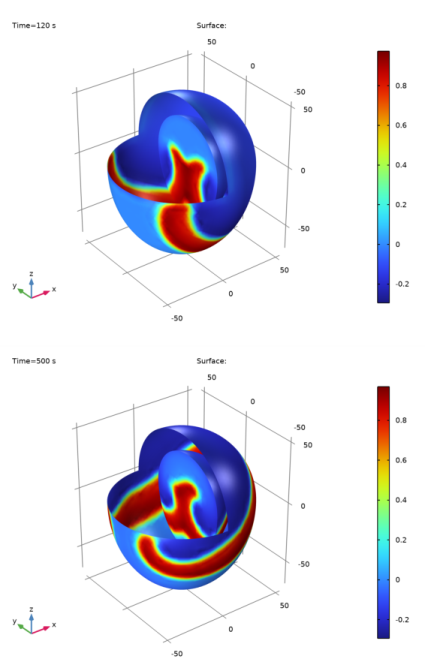
شکل 2: حل معادلات FitzHugh-Nagumo در زمان های t = 120 s (بالا) و t = 500 s (پایین).
معادلات گینزبورگ-لاندو
شکل 3 زیر گونه v 1 را در زمان های مختلف نشان می دهد.
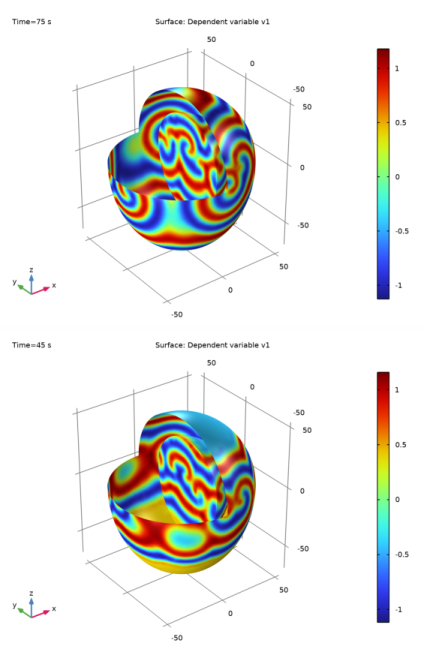
شکل 3: حل معادلات گینزبورگ-لانداو در زمان های t = 75 s (بالا) و t = 45 s (پایین).
پارامترهای معادله و شرایط اولیه مورد استفاده در اینجا باعث میشود گونههای در حال انتشار ( v 1 ) الگوهای مارپیچی مشخصی را با پیچیدگی فزاینده در طول زمان نمایش دهند.
منابع
1. FH Fenton، EM Cherry، HM Hastings، و SJ Evans، «شبیهسازیهای رایانهای بیدرنگ رسانههای تحریکپذیر: JAVA بهعنوان یک زبان علمی و بهعنوان بستهبندی برای برنامههای C و FORTRAN»، BioSystems، جلد . 64، صفحات 73-96، 2002.
2. Y. Kuramoto، نوسانات شیمیایی، امواج و آشفتگی ، انتشارات دوور، 2003.
3. جی کینر و جی اسنید، فیزیولوژی ریاضی ، اسپرینگر، 1998.
مسیر کتابخانه برنامه: COMSOL_Multiphysics/Equation_Based/heart_electrical
دستورالعمل مدلسازی
از منوی File ، New را انتخاب کنید .
جدید
در پنجره جدید ، روی  Model Wizard کلیک کنید .
Model Wizard کلیک کنید .
مدل جادوگر
1 | در پنجره Model Wizard ، روی |
2 | در درخت انتخاب فیزیک ، ریاضیات> رابط های PDE> فرم عمومی PDE (g) را انتخاب کنید . |
3 | روی افزودن کلیک کنید . |
4 | در قسمت متنی Number of varpendable variables ، 2 را تایپ کنید . |
5 |
6 | در درخت انتخاب مطالعه ، General Studies>Time Dependent را انتخاب کنید . |
7 |
ریشه
1 | در پنجره Model Builder ، روی گره ریشه کلیک کنید. |
2 | در پنجره تنظیمات گره ریشه ، بخش Unit System را پیدا کنید . |
3 | از لیست سیستم واحد ، هیچکدام را انتخاب کنید . |
معادلات در این مدل به صورت بدون بعد آورده شده است. خاموش کردن پشتیبانی واحد از هشدارهای مربوط به استفاده ناسازگار از واحدها جلوگیری می کند.
هندسه 1
دستورالعمل های زیر را برای ایجاد مجدد هندسه نشان داده شده در شکل 1 دنبال کنید .
کره 1 (sph1)
1 | در نوار ابزار Geometry ، روی |
2 | در پنجره تنظیمات برای Sphere ، بخش Size را پیدا کنید . |
3 | در قسمت متن Radius ، 54 را تایپ کنید . |
4 |
بیضی 1 (elp1)
1 | در نوار ابزار Geometry ، روی |
2 | در پنجره تنظیمات برای Ellipsoid ، بخش Size and Shape را پیدا کنید . |
3 | در قسمت متن a-semiaxis ، 54 را تایپ کنید . |
4 | در قسمت متن b-semiaxis ، 54 را تایپ کنید . |
5 | در قسمت متنی c-semiaxis 70 را تایپ کنید . |
6 |
سپس با ادغام نیمه بالایی کره با نیمه پایینی بیضی، جامد تخم مرغی شکل را ایجاد کنید. از بلوک ها برای حذف نیمه پایین کره و نیمه بالایی بیضی استفاده کنید.
بلوک 1 (blk1)
1 | در نوار ابزار Geometry ، روی |
2 | در پنجره تنظیمات برای Block ، قسمت Size and Shape را پیدا کنید . |
3 | در قسمت متن Width عدد 110 را تایپ کنید . |
4 | در قسمت Depth text عدد 110 را تایپ کنید . |
5 | در قسمت متن ارتفاع ، 110 را تایپ کنید . |
6 | قسمت Position را پیدا کنید . از لیست پایه ، مرکز را انتخاب کنید . |
7 | در قسمت متن z ، 55 را تایپ کنید . |
8 |
تفاوت 1 (dif1)
1 | در نوار ابزار Geometry ، روی |
2 | فقط شی elp1 را انتخاب کنید. |
3 | در پنجره تنظیمات برای تفاوت ، بخش تفاوت را پیدا کنید . |
4 | زیربخش اشیاء را برای تفریق پیدا کنید . برای انتخاب دکمه ضامن |
5 | فقط شی blk1 را انتخاب کنید. |
6 |
بلوک 2 (blk2)
1 | در نوار ابزار Geometry ، روی |
2 | در پنجره تنظیمات برای Block ، قسمت Size and Shape را پیدا کنید . |
3 | در قسمت متن Width عدد 110 را تایپ کنید . |
4 | در قسمت Depth text عدد 110 را تایپ کنید . |
5 | در قسمت متن ارتفاع ، 110 را تایپ کنید . |
6 | قسمت Position را پیدا کنید . از لیست پایه ، مرکز را انتخاب کنید . |
7 | در قسمت متن z ، -55 را تایپ کنید . |
8 |
تفاوت 2 (dif2)
1 | در نوار ابزار Geometry ، روی |
2 | فقط شیء sph1 را انتخاب کنید. |
3 | در پنجره تنظیمات برای تفاوت ، بخش تفاوت را پیدا کنید . |
4 | زیربخش اشیاء را برای تفریق پیدا کنید . برای انتخاب دکمه ضامن |
5 | فقط شی blk2 را انتخاب کنید. |
6 |
اتحادیه 1 (uni1)
1 | در نوار ابزار Geometry ، روی |
2 | در پنجره Graphics کلیک کنید و سپس Ctrl+A را فشار دهید تا هر دو شی انتخاب شوند. |
3 | در پنجره تنظیمات برای Union ، روی |
حالا حفره داخل قلب ایجاد کنید.
مقیاس 1 (sca1)
1 | در نوار ابزار Geometry ، روی |
2 | در پنجره تنظیمات برای مقیاس ، بخش ورودی را پیدا کنید . |
3 | چک باکس Keep input objects را انتخاب کنید . |
4 | فقط شی uni1 را انتخاب کنید. |
5 | بخش Scale Factor را پیدا کنید . در قسمت Factor text 2/3 را تایپ کنید . |
6 |
7 |
تفاوت 3 (dif3)
1 | در نوار ابزار Geometry ، روی |
2 | فقط شی uni1 را انتخاب کنید. |
3 | در پنجره تنظیمات برای تفاوت ، بخش تفاوت را پیدا کنید . |
4 | زیربخش اشیاء را برای تفریق پیدا کنید . برای انتخاب دکمه ضامن |
5 | فقط شیء sca1 را انتخاب کنید. |
6 |
مرحله بعدی ایجاد دیوار جداکننده دو اتاق است.
سیلندر 1 (cyl1)
1 | در نوار ابزار Geometry ، روی |
2 | در پنجره تنظیمات سیلندر ، بخش اندازه و شکل را پیدا کنید . |
3 | در قسمت متن Radius عدد 45 را تایپ کنید . |
4 | در قسمت متن ارتفاع ، 10 را تایپ کنید . |
5 | قسمت Position را پیدا کنید . در قسمت متن x ، -5 را تایپ کنید . |
6 | در قسمت متن z ، -5 را تایپ کنید . |
7 | قسمت Axis را پیدا کنید . از لیست نوع محور ، دکارتی را انتخاب کنید . |
8 | در قسمت متن x ، 1 را تایپ کنید . |
9 | در قسمت متن z ، 0 را تایپ کنید . |
10 |
اتحادیه 2 (uni2)
1 | در نوار ابزار Geometry ، روی |
2 | در پنجره Graphics کلیک کنید و سپس Ctrl+A را فشار دهید تا هر دو شی انتخاب شوند. |
3 | در پنجره تنظیمات برای Union ، بخش Union را پیدا کنید . |
4 | کادر تیک Keep interior borders را پاک کنید . |
5 |
این هندسه را کامل می کند.
تعاریف جهانی
پارامترهای 1
1 | در پنجره Model Builder ، در قسمت Global Definitions روی Parameters 1 کلیک کنید . |
2 | در پنجره تنظیمات برای پارامترها ، بخش پارامترها را پیدا کنید . |
3 | در جدول تنظیمات زیر را وارد کنید: |
نام | اصطلاح | ارزش | شرح |
آلفا | 0.1 | 0.1 | آستانه تحریک |
اپسیلون | 0.01 | 0.01 | تحریک پذیری |
بتا | 0.5 | 0.5 | پارامتر سیستم |
گاما | 1 | 1 | پارامتر سیستم |
دلتا | 0 | 0 | پارامتر سیستم |
V0 | 1 | 1 | ارزش بالقوه بالا |
اکنون 0 | 0.3 | 0.3 | افزایش ارزش بازدارنده |
د | 1e-5 | 1E-5 | فاصله شیفت خارج از محور |
از شرط مرزی پیش فرض نویمان در تمام مرزها استفاده کنید.
فرم عمومی PDE (G)
فرم عمومی PDE 1
1 | در پنجره Model Builder ، در قسمت Component 1 (comp1)>General Form PDE (g) روی General Form PDE 1 کلیک کنید . |
2 | در پنجره تنظیمات برای فرم عمومی PDE ، بخش Conservative Flux را پیدا کنید . |
3 | بردار Γ دوم را به عنوان مشخص کنید |
0 | ایکس |
0 | y |
0 | z |
4 | قسمت Source Term را پیدا کنید . در آرایه فیلد متنی f ، (alpha-u1)*(u1-1)*u1-u2 را در ردیف اول تایپ کنید. |
5 | در آرایه f text-field، epsilon*(beta*u1-gamma*u2-delta) را در ردیف دوم تایپ کنید. |
مقادیر اولیه 1
1 | در پنجره Model Builder ، روی مقادیر اولیه 1 کلیک کنید . |
2 | در پنجره تنظیمات برای مقادیر اولیه ، قسمت مقادیر اولیه را پیدا کنید . |
3 | در قسمت متنی u 1 ، V0*((x+d)>0)*((z+d)>0) را تایپ کنید . |
4 | در قسمت u 2 ، nu0*((-x+d)>0)*((z+d)>0) را تایپ کنید . |
مش 1
1 | در پنجره Model Builder ، در قسمت Component 1 (comp1) روی Mesh 1 کلیک کنید . |
2 | در پنجره تنظیمات مش ، قسمت Physics-Controlled Mesh را پیدا کنید . |
3 | از لیست اندازه عنصر ، Fine را انتخاب کنید . |
4 |  |
مطالعه 1
مرحله 1: وابسته به زمان
1 | در پنجره Model Builder ، در بخش مطالعه 1 ، روی Step 1: Time Dependent کلیک کنید . |
2 | در پنجره تنظیمات مربوط به زمان وابسته ، قسمت تنظیمات مطالعه را پیدا کنید . |
3 | در قسمت متنی زمان خروجی ، range(0,5,500) را تایپ کنید . |
4 | در نوار ابزار صفحه اصلی ، |
نتایج
گروه طرح سه بعدی 1
نمودار پیش فرض یک نمودار برش از متغیر وابسته را نشان می دهد. برای ایجاد نمودارهای ارائه شده در شکل 2 ، باید برخی از مرزها را سرکوب کنید.
مطالعه 1/راه حل 1 (sol1)
در پنجره Model Builder ، گره Results>Datasets را گسترش دهید ، سپس روی Study 1/Solution 1 (sol1) کلیک کنید .
انتخاب
1 | در نوار ابزار نتایج ، روی |
2 | در پنجره تنظیمات برای انتخاب ، قسمت انتخاب موجودیت هندسی را پیدا کنید . |
3 | از لیست سطح نهاد هندسی ، Boundary را انتخاب کنید . |
4 |
5 | در کادر محاوره ای Paste Selection ، 1 3 10-18 را در قسمت متن انتخاب تایپ کنید . |
6 | روی OK کلیک کنید . |
7 | در پنجره تنظیمات برای انتخاب ، قسمت انتخاب موجودیت هندسی را پیدا کنید . |
8 |
9 | در کادر گفتگوی Create Selection ، روی OK کلیک کنید . |
گروه طرح سه بعدی 2
1 | در نوار ابزار نتایج ، روی |
2 | در پنجره Settings for 3D Plot Group ، قسمت Plot Settings را پیدا کنید . |
3 | کادر بررسی لبه های مجموعه داده Plot را پاک کنید . |
سطح 1
1 | روی 3D Plot Group 2 کلیک راست کرده و Surface را انتخاب کنید . |
2 | در نوار ابزار 3D Plot Group 2 ، روی |
3 |
گروه طرح سه بعدی 2
1 | در پنجره Model Builder ، روی 3D Plot Group 2 کلیک کنید . |
2 | در پنجره Settings for 3D Plot Group ، بخش Data را پیدا کنید . |
3 | از لیست زمان (ها) ، 120 را انتخاب کنید . |
4 | در نوار ابزار 3D Plot Group 2 ، روی |
این مدل سازی معادلات فیتز هیو-ناگومو را کامل می کند. برای مدل سازی معادلات پیچیده لاندو-گینزبورگ از مجموعه دستورالعمل های زیر استفاده کنید.
فیزیک را اضافه کنید
1 | در نوار ابزار Home ، روی |
2 | به پنجره Add Physics بروید . |
3 | در درخت، Mathematics>PDE Interfaces>General Form PDE (g) را انتخاب کنید . |
4 | برای گسترش بخش Dependent Variables کلیک کنید . در قسمت متن نام فیلد ، v را تایپ کنید . |
5 | در قسمت متنی Number of varpendable variables ، 2 را تایپ کنید . |
6 | در جدول متغیرهای وابسته ، تنظیمات زیر را وارد کنید: |
v1 |
7 | رابط های فیزیک را در زیربخش مطالعه بیابید . در جدول، کادر حل را برای مطالعه 1 پاک کنید . |
8 | روی Add to Component 1 در نوار ابزار پنجره کلیک کنید . |
9 | در نوار ابزار Home ، روی |
اضافه کردن مطالعه
1 | در نوار ابزار Home ، روی |
2 | به پنجره Add Study بروید . |
3 | رابط های فیزیک را در زیربخش مطالعه بیابید . در جدول، کادر حل را برای فرم عمومی PDE (g) پاک کنید . |
4 | زیربخش مطالعات را پیدا کنید . در درخت انتخاب مطالعه ، General Studies>Time Dependent را انتخاب کنید . |
5 | روی Add Study در نوار ابزار پنجره کلیک کنید . |
6 | در نوار ابزار Home ، روی |
تعاریف جهانی
پارامترهای 1
1 | در پنجره Model Builder ، در قسمت Global Definitions روی Parameters 1 کلیک کنید . |
2 | در پنجره تنظیمات برای پارامترها ، بخش پارامترها را پیدا کنید . |
3 | در جدول تنظیمات زیر را وارد کنید: |
نام | اصطلاح | ارزش | شرح |
c1 | 2 | 2 | پارامتر PDE |
ج3 | -0.2 | -0.2 | پارامتر PDE |
فرم عمومی PDE 2 (G2)
دقت محلول را می توان با استفاده از عناصر مکعبی هرمیت به جای عناصر درجه دوم لاگرانژ بهبود بخشید.
1 | در پنجره Model Builder ، در قسمت Component 1 (comp1) روی General Form PDE 2 (g2) کلیک کنید . |
2 | در پنجره تنظیمات برای فرم عمومی PDE ، برای گسترش بخش Discretization کلیک کنید . |
3 | از لیست نوع تابع شکل ، Hermite را انتخاب کنید . |
فرم عمومی PDE 1
در این مورد نیز از شرط مرزی پیشفرض نویمان در تمام مرزها استفاده کنید.
1 | در پنجره Model Builder ، در قسمت Component 1 (comp1)>General Form PDE 2 (g2) روی General Form PDE 1 کلیک کنید . |
2 | در پنجره تنظیمات برای فرم عمومی PDE ، بخش Conservative Flux را پیدا کنید . |
3 | اولین بردار Γ را به صورت مشخص کنید |
-v1x+c1*v2x | ایکس |
-v1y+c1*v2y | y |
-v1z+c1*v2z | z |
4 | بردار Γ دوم را به عنوان مشخص کنید |
-c1*v1x-v2x | ایکس |
-c1*v1y-v2y | y |
-c1*v1z-v2z | z |
5 | قسمت Source Term را پیدا کنید . در آرایه f text-field، v1-(v1-c3*v2)*(v1^2+v2^2) را در ردیف اول تایپ کنید. |
6 | در آرایه f text-field، v2-(c3*v1+v2)*(v1^2+v2^2) را در ردیف دوم تایپ کنید. |
مقادیر اولیه 1
1 | در پنجره Model Builder ، روی مقادیر اولیه 1 کلیک کنید . |
2 | در پنجره تنظیمات برای مقادیر اولیه ، قسمت مقادیر اولیه را پیدا کنید . |
3 | در قسمت متن v 1 ، tanh(z[1/m]) را تایپ کنید . |
4 | در قسمت متن v 2 ، -tanh(z[1/m]) را تایپ کنید . |
تلرانس های نسبی و مطلق را با ضریب 10 تشدید کنید.
مطالعه 2
مرحله 1: وابسته به زمان
1 | در پنجره Model Builder ، در زیر مطالعه 2 ، روی Step 1: Time Dependent کلیک کنید . |
2 | در پنجره تنظیمات مربوط به زمان وابسته ، قسمت تنظیمات مطالعه را پیدا کنید . |
3 | در قسمت متن زمان خروجی ، range(0,5,75) را تایپ کنید . |
4 | از لیست Tolerance ، User controlled را انتخاب کنید . |
5 | در قسمت متنی Relative tolerance ، 0.001 را تایپ کنید . |
راه حل 2 (sol2)
1 | در نوار ابزار مطالعه ، روی |
2 | در پنجره Model Builder ، گره Solution 2 (sol2) را گسترش دهید ، سپس روی Time-Dependent Solver 1 کلیک کنید . |
3 | در پنجره تنظیمات برای حل وابسته به زمان ، برای گسترش بخش تحمل مطلق کلیک کنید . |
4 | از لیست روش تحمل ، دستی را انتخاب کنید . |
5 | در قسمت متنی Absolute tolerance ، 0.0001 را تایپ کنید . |
6 | در نوار ابزار مطالعه ، |
نتایج
دستورالعمل ها را برای ایجاد نمودارهای داده شده در شکل 3 دنبال کنید .
مطالعه 2/راه حل 2 (sol2)
در پنجره Model Builder ، در بخش Results>Datasets روی Study 2/Solution 2 (sol2) کلیک کنید .
انتخاب
1 | در نوار ابزار نتایج ، روی |
2 | در پنجره تنظیمات برای انتخاب ، قسمت انتخاب موجودیت هندسی را پیدا کنید . |
3 | از لیست سطح نهاد هندسی ، Boundary را انتخاب کنید . |
4 | از لیست Selection ، Explicit 1 را انتخاب کنید . |
گروه طرح سه بعدی 4
1 | در نوار ابزار نتایج ، روی |
2 | در پنجره Settings for 3D Plot Group ، بخش Data را پیدا کنید . |
3 | از لیست مجموعه داده ، مطالعه 2/راه حل 2 (sol2) را انتخاب کنید . |
4 | قسمت Plot Settings را پیدا کنید . کادر بررسی لبه های مجموعه داده Plot را پاک کنید . |
سطح 1
1 | روی 3D Plot Group 4 کلیک راست کرده و Surface را انتخاب کنید . |
2 | در پنجره تنظیمات برای Surface ، روی Replace Expression در گوشه سمت راست بالای بخش Expression کلیک کنید . از منو، Component 1 (comp1)>General Form PDE 2>v1 – Dependent variable v1 را انتخاب کنید . |
3 | در نوار ابزار 3D Plot Group 4 ، روی |
گروه طرح سه بعدی 4
1 | در پنجره Model Builder ، روی 3D Plot Group 4 کلیک کنید . |
2 | در پنجره Settings for 3D Plot Group ، بخش Data را پیدا کنید . |
3 | از لیست زمان (ها) ، 45 را انتخاب کنید . |
4 | در نوار ابزار 3D Plot Group 4 ، روی |
1
توجه داشته باشید که با استفاده از قابلیتهای واردات CAD، میتوان هندسههای واقعیتر قلب انسان/حیوان، با ناهمسانگردیها و ناهمگنیها و همچنین ابعاد مناسبتر را به COMSOL Multiphysics وارد کرد.
2
با تکمیل این مرحله، جایگزینی معادلات نسبتاً ساده با یک مدل ریاضی فیزیولوژیکی واقعی تر نیز ساده خواهد بود.




