 |
دومین نسل هارمونیک پرتو گاوسی
معرفی
سیستم های لیزری یک حوزه کاربردی مهم در الکترونیک مدرن هستند. راه‌های مختلفی برای تولید پرتو لیزر وجود دارد، اما همه آنها یک چیز مشترک دارند: طول موج توسط انتشار تحریک شده تعیین می‌شود که به پارامترهای ماده بستگی دارد. به ویژه یافتن لیزرهایی که طول موج های کوتاه تولید می کنند (مثلاً نور ماوراء بنفش) دشوار است. با مواد غیر خطی می توان هارمونیک هایی با فرکانس هایی که مضرب فرکانس نور لیزر هستند تولید کرد. نور منسجم با نصف طول موج پرتو اصلی با مواد غیرخطی درجه دوم تولید می شود. این مدل نحوه تنظیم نسل دوم هارمونیک را به عنوان شبیه سازی موج گذرا با استفاده از خواص غیرخطی مواد نشان می دهد. A Nd:YAG ( λ = 1.06 μم) پرتو لیزر بر روی یک کریستال غیر خطی متمرکز شده است، به طوری که کمر پرتو در داخل کریستال قرار می گیرد.
تعریف مدل
برای ساده کردن مشکل و صرفه جویی در زمان محاسبه، این مدل یک شبیه سازی سه بعدی کامل نیست، بلکه یک مدل دو بعدی است. این مدل از سیستم مختصات دوبعدی استاندارد COMSOL Multiphysics استفاده می‌کند، با فرض اینکه پرتو در جهت x منتشر می‌شود، وابستگی به شدت گاوسی عرضی در جهت y دارد و میدان الکتریکی در جهت خارج از صفحه z قطبی شده است .
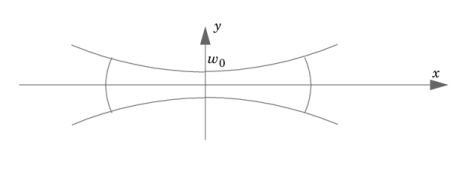
هنگامی که یک پرتو لیزر منتشر می شود، به صورت یک موج مسطح تقریبی با شدت مقطع گاوسی حرکت می کند. در نقطه کانونی، پرتو لیزر دارای حداقل عرض، w 0 است . برای یک پرتو گاوسی با حداقل شعاع نقطه ای که در مقایسه با طول موج خیلی کوچک نیست ( w 0 > λ )، حل معادلات ماکسول هماهنگ با زمان برای یک هندسه دو بعدی 1 را می توان با حل تحلیلی زیر تقریب زد. معادله موج 2 :
جایی که
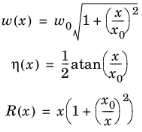
در این عبارات، w 0 حداقل کمر، ω فرکانس زاویه ای، y مختصات عرضی درون صفحه و k عدد موج است. جبهه موج پرتو دقیقاً مسطح نیست. مانند یک موج کروی با شعاع R ( x ) منتشر می شود . با این حال، نزدیک به نقطه کانونی، موج تقریباً صاف است.
پرتو لیزر نیز به عنوان یک پالس در زمان، با استفاده از تابع پوشش گاوسی مدل‌سازی می‌شود. این یک بسته موج با طیف فرکانس گاوسی تولید می کند.
این عبارات به عنوان شرایط مرزی ورودی استفاده می شود.
خواص غیر خطی برای تولید هارمونیک دوم در یک ماده را می توان با ماتریس زیر تعریف کرد:
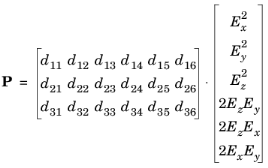
جایی که P قطبش است. مدل فقط از پارامتر d 33 برای سادگی استفاده می کند. برای کوچک نگه داشتن اندازه مسئله، پارامتر غیرخطی با چند مرتبه بزرگ‌نمایی می‌شود. کریستال در اینجا دارای مقدار 10-17 F /V است ، زمانی که مقادیر بیشتر مواد معمولاً در محدوده 10-22 F/ V هستند . بدون این بزرگ‌نمایی، برای به دست آوردن یک هارمونیک دوم قابل تشخیص نیاز به فاصله انتشار بسیار طولانی‌تری دارد که منجر به یک مشکل محاسباتی بزرگ می‌شود.
اندازه مش برای حل نه تنها طول موج اصلی، بلکه برای طول موج دوم هارمونیک تعریف شده است. با توجه به اندازه مش، مرحله زمانی به صورت محاسبه می شود
،که در آن CFL به اصطلاح عدد CFL است – به نام کورانت، فریدریش و لوی – h max حداکثر اندازه عنصر مش است و c 0 سرعت نور است. در این مدل از عدد CFL 0.15 استفاده شده است. به طور کلی باید در محدوده 0.1 تا 0.2 باشد. برای اطلاعات بیشتر در مورد نحوه تعریف گام زمانی برای حلگر وابسته به زمان، رجوع کنید به Ref. 2 .
نتایج و بحث
هدف اصلی این شبیه سازی محاسبه دومین نسل هارمونیک زمانی است که پالس در امتداد هندسه 20 میکرومتر حرکت می کند . بنابراین باید مدت زمانی را که طول می کشد تا پالس وارد شود، عبور کند و از ولوم ناپدید شود را حل کنید. پالس دارای زمان مشخصه 10 fs است و در زیر می توانید پالس را پس از 61 fs طی کنید.
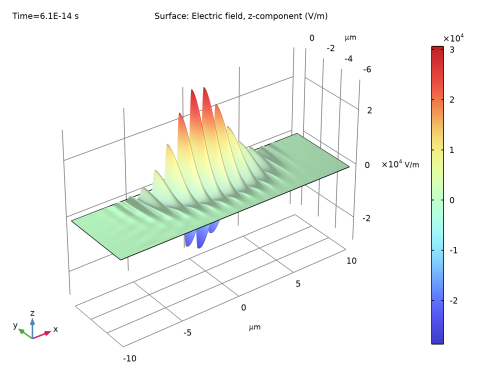
شکل 1: نبض پس از 61 fs.
پس از 90 fs، پالس به مرز خروجی رسیده است ( شکل 2 را ببینید ). شبیه سازی باید 30 fs دیگر ادامه یابد تا زمانی که پالس به طور کامل ناپدید شود.
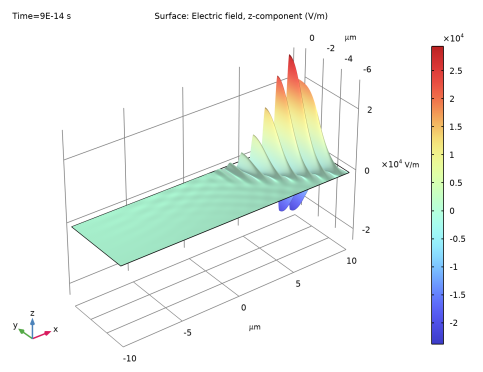
شکل 2: نبض پس از 90 fs. اکنون به مرز خروجی رسیده است.
شبیه سازی زمان های بین 60 fs و 120 fs را ذخیره می کند، یعنی زمانی که پالس از مرز خروجی عبور می کند. میدان الکتریکی در این مرز دارای یک جزء هارمونیک دوم است که می تواند با استفاده از تحلیل فرکانس استخراج شود. نتیجه در شکل 3 نشان داده شده است . قله کوچک در سمت راست قله بزرگ دومین نسل هارمونیک است. در سمت چپ قله بزرگ نیز یک قله کوچکتر وجود دارد که به دلیل تولید فرکانس اختلاف است. این اثر تصحیح نوری نیز یک فرآیند نوری غیرخطی مرتبه دوم است.
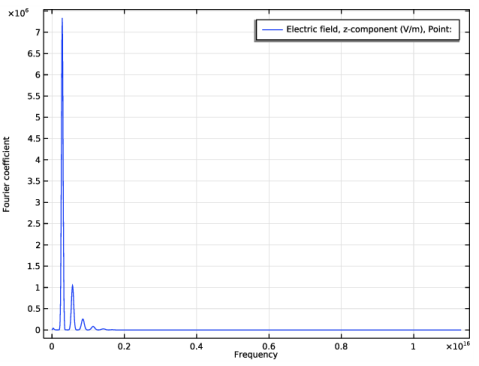
شکل 3: طیف فرکانس پرتو در مرز خروجی. قله سمت راست قله بزرگ نسل دوم هارمونیک است. همچنین پیک های کوچکتری برای هارمونیک های بالاتر پیدا می کنید. همچنین یک پیک کوچک نزدیک به فرکانس صفر وجود دارد که به دلیل تولید فرکانس اختلاف است.
ارجاع
1. A. Yariv, Quantum Electronics , 3rd Edition, John Wiley & Sons, 1988.
2. COMSOL Knowledge Base 1118, “Resolving Time-dependent Waves,” https://www.comsol.com/support/knowledgebase/1118/ .
مسیر کتابخانه برنامه: RF_Module/Tutorials /second_harmonic_generation
دستورالعمل های مدل سازی
از منوی File ، New را انتخاب کنید .
جدید
در پنجره جدید ، روی 
Model Wizard کلیک کنید .
Model Wizard کلیک کنید .مدل جادوگر
1 | در پنجره Model Wizard روی  2D کلیک کنید . |
2 | در درخت انتخاب فیزیک ، فرکانس رادیویی > امواج الکترومغناطیسی، گذرا (temw) را انتخاب کنید . |
3 | روی افزودن کلیک کنید . |
4 |  روی مطالعه کلیک کنید . |
5 | در درخت انتخاب مطالعه ، General Studies>Time Dependent را انتخاب کنید . |
6 |  روی Done کلیک کنید . |
هندسه 1
1 | در پنجره Model Builder ، در قسمت Component 1 (comp1) روی Geometry 1 کلیک کنید . |
2 | در پنجره تنظیمات هندسه ، بخش Units را پیدا کنید . |
3 | از لیست واحد طول ، میکرومتر را انتخاب کنید . |
تعاریف جهانی
پارامترهای 1
1 | در پنجره Model Builder ، در قسمت Global Definitions روی Parameters 1 کلیک کنید . |
2 | در پنجره تنظیمات برای پارامترها ، بخش پارامترها را پیدا کنید . |
3 | در جدول تنظیمات زیر را وارد کنید: |
نام | اصطلاح | ارزش | شرح |
w0 | 2 [یک] | 2E-6 متر | حداقل شعاع نقطه ای پرتو لیزر |
lda0 | 1.06 [یک] | 1.06E-6 متر | طول موج پرتو لیزر ورودی |
E0 | 30 [کیلو ولت بر متر] | 30000 ولت بر متر | اوج میدان الکتریکی |
x0 | pi*w0^2/lda0 | 1.1855E-5 متر | محدوده ریلی |
k0 | 2*pi/lda0 | 5.9275E6 1/m | ثابت انتشار |
امگا 0 | k0*c_const | 1.777E15 1/s | فرکانس زاویه ای |
t0 | 25[fs] | 2.5E-14s | تاخیر زمانی نبض |
dt | 10[fs] | 1E-14 p | عرض پالس |
d33 | 1e-17[F/V] | 1E-17 s 7 A³/(kg² m 4 ) | عنصر ماتریس برای نسل دوم هارمونیک |
lda2 | lda0/2 | 5.3E-7 متر | طول موج برای هارمونیک دوم |
hmax | lda2/6 | 8.8333E-8 متر | حداکثر اندازه عنصر مش |
CFL | 0.15 | 0.15 | شماره CFL |
tstep | CFL*hmax/c_const | 4.4197E-17 s | مرحله زمانی |
چهار پارامتر آخر برای تعریف حداکثر اندازه عنصر مش و برای تعریف مرحله زمانی برای حل کننده وابسته به زمان استفاده می شود.
تحلیلی 1 (an1)
1 | در نوار ابزار Home ، روی  Functions کلیک کنید و Global>Analytic را انتخاب کنید . |
2 | در پنجره تنظیمات برای تحلیل ، w را در قسمت متن نام تابع تایپ کنید . |
3 | قسمت Definition را پیدا کنید . در قسمت متن Expression ، w0*sqrt(1+(x/x0)^2) را تایپ کنید . |
4 | قسمت Units را پیدا کنید . در جدول تنظیمات زیر را وارد کنید: |
بحث و جدل | واحد |
ایکس | متر |
5 | در قسمت متن تابع ، m را تایپ کنید . |
تحلیلی 2 (an2)
1 | در نوار ابزار Home ، روی  Functions کلیک کنید و Global>Analytic را انتخاب کنید . |
2 | در پنجره تنظیمات برای تحلیل ، eta را در قسمت متن نام تابع تایپ کنید . |
3 | قسمت Definition را پیدا کنید . در قسمت متن Expression ، atan2(x,x0)/2 را تایپ کنید . |
4 | قسمت Units را پیدا کنید . در جدول تنظیمات زیر را وارد کنید: |
بحث و جدل | واحد |
ایکس | متر |
5 | در قسمت Function text، rad را تایپ کنید . |
تحلیلی 3 (an3)
1 | در نوار ابزار Home ، روی  Functions کلیک کنید و Global>Analytic را انتخاب کنید . |
2 | در پنجره تنظیمات برای تحلیل ، R را در قسمت متن نام تابع تایپ کنید . |
3 | قسمت Definition را پیدا کنید . در قسمت متن Expression ، x*(1+(x0/x)^2) را تایپ کنید . |
4 | قسمت Units را پیدا کنید . در جدول تنظیمات زیر را وارد کنید: |
بحث و جدل | واحد |
ایکس | متر |
5 | در قسمت متن تابع ، m را تایپ کنید . |
هندسه 1
یک دامنه محاسبه مستطیلی ایجاد کنید، جایی که y = 0 صفحه تقارن پرتو لیزر است.
مستطیل 1 (r1)
1 | در نوار ابزار Geometry ، روی  Rectangle کلیک کنید . |
2 | در پنجره تنظیمات برای Rectangle ، بخش Size and Shape را پیدا کنید . |
3 | در قسمت متن Width عدد 20 را تایپ کنید . |
4 | در قسمت متن ارتفاع ، 6 را تایپ کنید . |
5 | قسمت Position را پیدا کنید . در قسمت متن x ، -10 را تایپ کنید . |
6 | در قسمت متن y ، -6 را تایپ کنید . |
7 |  روی Build All Objects کلیک کنید . |
8 |  روی دکمه Zoom Extents در نوار ابزار Graphics کلیک کنید . |
مواد
فرض کنید که پرتو لیزر از طریق یک ماده مصنوعی با خواص هوا به جز یک غیرخطی نوری درجه دوم اضافی منتشر می شود. بعداً هنگام تنظیم معادله موج، غیرخطی بودن را مشخص خواهید کرد.
مواد را اضافه کنید
1 | در نوار ابزار Home ، روی  Add Material کلیک کنید تا پنجره Add Material باز شود . |
2 | به پنجره Add Material بروید . |
3 | در درخت، Built-in>Air را انتخاب کنید . |
4 | روی Add to Component در نوار ابزار پنجره کلیک کنید . |
5 | در نوار ابزار Home ، روی  Add Material کلیک کنید تا پنجره Add Material بسته شود . |
امواج الکترومغناطیسی، گذرا (TEMW)
فقط برای جزء خارج از صفحه حل کنید.
1 | در پنجره Model Builder ، در قسمت Component 1 (comp1) روی امواج الکترومغناطیسی ، گذرا (temw) کلیک کنید . |
2 | در پنجره تنظیمات برای امواج الکترومغناطیسی ، گذرا ، قسمت Components را پیدا کنید . |
3 | از اجزای میدان الکتریکی حل شده برای لیست، بردار خارج از صفحه را انتخاب کنید . |
رسانای مغناطیسی کامل 1
1 | در نوار ابزار Physics ، روی  Boundaries کلیک کنید و Perfect Magnetic Conductor را انتخاب کنید . |
2 | فقط مرز 3 را انتخاب کنید. |
شرایط مرزی پراکندگی 1
1 | در نوار ابزار Physics ، روی  Boundaries کلیک کنید و Scattering Boundary Condition را انتخاب کنید . |
2 | فقط مرز 1 را انتخاب کنید. |
3 | در پنجره تنظیمات برای شرایط مرزی پراکندگی ، بخش شرایط مرزی پراکندگی را پیدا کنید . |
4 | از لیست فیلد حادثه ، موج داده شده توسط فیلد E را انتخاب کنید . |
5 | بردار E 0 را به صورت مشخص کنید |
0 | ایکس |
0 | y |
E0*sqrt(w0/w(x))*exp(-y^2/w(x)^2)*cos(omega0*t-k0*x+eta(x)-k0*y^2/(2 *R(x))*exp(-(t-t0)^2/dt^2) | z |
شرایط مرزی پراکندگی 2
1 | در نوار ابزار Physics ، روی  Boundaries کلیک کنید و Scattering Boundary Condition را انتخاب کنید . |
2 | فقط مرز 4 را انتخاب کنید. |
معادله موج، الکتریک 1
1 | در پنجره Model Builder ، روی Wave Equation, Electric 1 کلیک کنید . |
2 | در پنجره تنظیمات برای معادله موج ، Electric ، بخش Electric Displacement Field را پیدا کنید . |
3 | از لیست مدل میدان جابجایی الکتریکی ، جابجایی الکتریکی باقیمانده را انتخاب کنید . |
4 | بردار D r را به صورت مشخص کنید |
0 | ایکس |
0 | y |
d33*temw.Ez^2 | z |
مش 1
نقشه برداری 1
در نوار ابزار Mesh ، روی Mapped کلیک کنید .
Mapped کلیک کنید .توزیع 1
1 | روی Mapped 1 کلیک راست کرده و Distribution را انتخاب کنید . |
2 | فقط مرزهای 1 و 4 را انتخاب کنید. |
3 | در پنجره تنظیمات برای توزیع ، بخش توزیع را پیدا کنید . |
4 | از لیست نوع توزیع ، Explicit را انتخاب کنید . |
5 | در قسمت نسبی قرارگیری رئوس در امتداد فیلد متن لبه ، sin(range(0,0.025*pi,0.5*pi)) را تایپ کنید . این باعث ایجاد یک شبکه متراکم تر به مرز بالایی می شود. |
اندازه
1 | در پنجره Model Builder ، در قسمت Component 1 (comp1)>Mesh 1 روی Size کلیک کنید . |
2 | در پنجره تنظیمات برای اندازه ، قسمت اندازه عنصر را پیدا کنید . |
3 | روی دکمه Custom کلیک کنید . |
4 | قسمت پارامترهای اندازه عنصر را پیدا کنید . در قسمت حداکثر اندازه عنصر ، hmax را تایپ کنید . |
5 |  روی ساخت همه کلیک کنید . |
6 |  روی دکمه Zoom Extents در نوار ابزار Graphics کلیک کنید . |
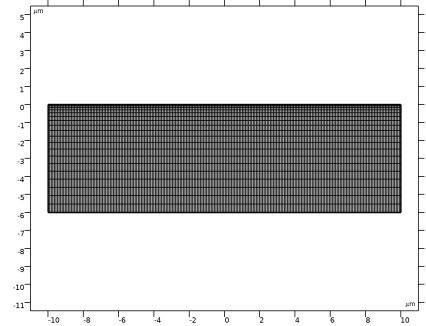تعاریف
برای انجام یک تحلیل FFT، تعداد مراحل زمانی که باید ذخیره شوند بسیار زیاد است. برای ذخیره تمام راه حل های فیلد A در یک فایل مدل بزرگ نتیجه می شود. با این حال، برای FFT، فقط نگاه کردن به میدان در مرز خروجی جالب است. شما می‌توانید با تعریف یک Domain Point Probe که میدان الکتریکی روی محور را در مرز خروجی ذخیره و نمایش می‌دهد از این واقعیت استفاده کنید، در حالی که میدان A فقط در زمان‌های تعریف‌شده در مطالعه ذخیره می‌شود.
Domain Point Probe 1
1 | در نوار ابزار تعاریف ، روی  Probes کلیک کنید و Domain Point Probe را انتخاب کنید . |
2 | در پنجره تنظیمات برای Domain Point Probe ، قسمت Point Selection را پیدا کنید . |
3 | در ردیف مختصات ، x را روی 10 تنظیم کنید . |
عبارت Point Probe 1 (ppb1)
1 | در پنجره Model Builder ، گره Domain Point Probe 1 را گسترش دهید ، سپس روی Point Probe Expression 1 (ppb1) کلیک کنید . |
2 | در پنجره تنظیمات برای Point Probe Expression ، Eout را در قسمت متن نام متغیر تایپ کنید . |
3 | روی Replace Expression در گوشه سمت راست بالای بخش Expression کلیک کنید . از منو، Component 1 (comp1)>Electromagnetic Waves، Transient>Electric>Electric field – V/m>temw.Ez – Electric field، z-component را انتخاب کنید . |
مطالعه 1
مرحله 1: وابسته به زمان
اکنون زمان هایی را برای ذخیره راه حل های کامل فیلد مشخص کنید.
1 | در پنجره Model Builder ، در بخش مطالعه 1 ، روی Step 1: Time Dependent کلیک کنید . |
2 | در پنجره تنظیمات مربوط به زمان وابسته ، قسمت تنظیمات مطالعه را پیدا کنید . |
3 | در قسمت متنی بار خروجی ، 0 61[fs] 90[fs] 120[fs] را تایپ کنید . |
4 | برای گسترش بخش Results while Solving کلیک کنید . کادر Plot را انتخاب کنید . |
راه حل 1 (sol1)
1 | در نوار ابزار مطالعه ، روی  Show Default Solver کلیک کنید . |
حل کننده را تنظیم کنید تا فیلد خروجی را هر 0.2 fs محاسبه کند.
2 | در پنجره Model Builder ، گره Solution 1 (sol1) را گسترش دهید ، سپس روی Time-Dependent Solver 1 کلیک کنید . |
3 | در پنجره تنظیمات برای حل وابسته به زمان ، برای گسترش بخش Time Steping کلیک کنید . |
4 | از لیست مراحل انجام شده توسط حل کننده ، دستی را انتخاب کنید . |
5 | در قسمت متنی Time step ، tstep را تایپ کنید . |
6 | در نوار ابزار مطالعه ،  روی محاسبه کلیک کنید . |
نتایج
گروه طرح دو بعدی 1
اکنون نمودارهای سطح را همانطور که در شکل 1 و شکل 2 نشان داده شده است، تعریف کنید .
سطح 1
1 | در پنجره Model Builder ، گره 2D Plot Group 1 را گسترش دهید ، سپس روی Surface 1 کلیک کنید . |
2 | در پنجره تنظیمات برای Surface ، روی Replace Expression در گوشه سمت راست بالای بخش Expression کلیک کنید . از منو، temw.Ez – میدان الکتریکی ، z-component – V/m را انتخاب کنید . |
بیان قد 1
روی Surface 1 کلیک راست کرده و Height Expression را انتخاب کنید .
گروه طرح دو بعدی 1
1 | در پنجره Settings for 2D Plot Group ، بخش Data را پیدا کنید . |
2 | از لیست زمان (ها) ، 6.1E-14 را انتخاب کنید . |
3 | در نوار ابزار 2D Plot Group 1 ، روی  Plot کلیک کنید . اکنون باید طرح را در شکل 1 ببینید . |
4 | از لیست زمان (ها) ، 9E-14 را انتخاب کنید . |
5 | در نوار ابزار 2D Plot Group 1 ، روی  Plot کلیک کنید . اکنون باید طرح را در شکل 2 ببینید . |
نمودار جدول پروب 1
در نهایت، یک تحلیل طیفی از میدان الکتریکی روی محور در مرز خروجی انجام دهید.
1 | در پنجره Model Builder ، گره Results>Probe Plot Group 2 را گسترش دهید ، سپس روی Probe Table Graph 1 کلیک کنید . |
2 | در پنجره تنظیمات برای نمودار جدول ، بخش داده را پیدا کنید . |
3 | از لیست Transformation ، تبدیل فوریه گسسته را انتخاب کنید . |
4 | از فهرست نمایش ، طیف فرکانس را انتخاب کنید . |
5 | کادر بررسی محدوده فرکانس را انتخاب کنید . |
6 | در نوار ابزار Probe Plot Group 2 ، روی  Plot کلیک کنید . |
Probe Plot Group 2
اکنون باید نموداری مشابه تصویر 3 داشته باشید .
1
توجه کنید که میدان الکتریکی برای یک پرتو گاوسی دو بعدی تعریف شده است. در 2 بعدی، دامنه به عنوان ریشه دوم نسبت شعاع نقطه و تغییر فاز Gouy η ( x ) با ضریب 1/2 تعریف می شود. در سه بعدی دامنه فقط با استفاده از نسبت شعاع نقطه ای تعریف می شود و هیچ ضریب 1/2 برای تغییر فاز Gouy وجود ندارد.
2
در معادله موج پاراکسیال مشتق دوم با توجه به مختصات در جهت انتشار نادیده گرفته شده است. این تقریب از معادله هلمهولتز برای یک پرتو به شدت واگرا، مانند پرتویی که به شعاع نقطه ای بسیار کوچک متمرکز شده است ( w 0 < λ ) قابل استفاده نیست.
