تصمیمگیری در مورد نحوه مدلسازی انتقال بار در الکترولیت معمولاً نقطه شروع هنگام تنظیم یک مدل الکتروشیمیایی است زیرا تعیین میکند از چه رابط فیزیک هنگام شروع ساخت مدل خود استفاده کنید. توضیحات نظری متفاوتی از چگالی جریان الکترولیت در COMSOL Multiphysics گنجانده شده است. همانطور که در این بخش توضیح داده شد، آنها در شرایط مختلف قابل اجرا هستند.
میدان جابجایی الکتریکی در یک محیط با چگالی بار محلی مطابق با قانون گاوس، یکی از معادلات ماکسول، مرتبط است:
در الکترولیتها، معمولاً میتوان فرض کرد که گذردهی الکتریکی ثابت و برابر با مقدار توده است:
از این رو
در یک الکترولیت با حامل های بار یونی، چگالی بار را می توان به صورت زیر نوشت:
از این رو
این معادله پواسون است که پتانسیل الکترولیت را به توزیع حامل های بار درون الکترولیت مرتبط می کند. در اشتقاق آن فرض کردیم که تنها حامل های بار یون ها هستند و یون های حل شده و میدان الکتریکی گذردهی محیط را تغییر نمی دهند.
انتقال جرم حامل های بار در سیستم های آبی معمولاً توسط معادلات نرنست-پلانک به دست می آید . این معادلات از فعل و انفعالات یون-یون غفلت می کنند و بنابراین آنها فقط برای محلول های بی نهایت رقیق دقیق هستند:
توجه داشته باشید که سیستمهای الکترولیت متمرکز، مانند سیستمهای موجود در بسیاری از باتریها، از تعریف شار گونهای متمرکز بر اساس مجموعه معادلات ماکسول-استفان استفاده میکنند. این منجر به مجموعه متفاوتی از معادلات برای حل خواهد شد، اما اصول کلی و نتیجه گیری در این بخش یکسان خواهد بود.
با جایگزینی رابطه نرنست-اینشتین به جای تحرک الکتریکی یک یون، دریافت می کنیم:
عبارات بالا برای n گونه i ، همراه با معادله پواسون، مجموعه ای از n +1 معادله را در n +1 مجهول به دست می دهند. این معادلات نرنست-پلانک-پواسون هستند . آنها را می توان در COMSOL Multiphysics با جفت کردن حمل و نقل گونه های رقیق شده با الکترواستاتیک ، یا با استفاده از توزیع جریان سوم، رابط Nernst-Planck با مدل نگهداری شارژ تعریف کرد: پواسون ، اما آنها بسیار غیرخطی هستند و به سختی همگرا می شوند. اغلب، تقریب های بیشتر می تواند مشکل را بدون به خطر انداختن دقت ساده کند.
|
یک کمیت بعدی مهم که در معادله پواسون وجود دارد عبارت است از:
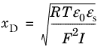
این طولی است که میدان های الکتریکی در سراسر آن غربال می شوند. به آن طول Debye می گویند . این طول در محلول های الکترولیت بسیار کوتاه است: برای یک قدرت یونی معمولی، این طول در حد 1 نانومتر است. الکتریسیته در فواصل بسیار بزرگتر از 1 نانومتر از سطح باردار وجود دارد:
محدودیت خنثی الکتریکی را می توان به عنوان شرط تعیین پتانسیل الکتریکی در معادلات نرنست-پلانک، به جای معادله کامل پواسون استفاده کرد. معادلات Nernst-Planck با الکتروخنثی برای توصیف جریان جریان در توزیع جریان سوم، رابط Nernst-Planck استفاده می شود.
توزیع جریان سوم، رابط Nernst-Planck |
خود جریان جریان به وسیله:
از جایگزینی عبارات نرنست-پلانک برای Ni ، قوانین بقای جرم و بار ترکیب می شوند تا به طور خودکار بقای جریان را برآورده کنند .
ما می توانیم با در نظر گرفتن عبارت ایجاد شده برای i l با جزئیات بیشتر، سیستم را ساده تر کنیم :
واضح است که سمت راست ترین عبارت صفر است: یعنی جابجایی یک محلول الکتروخنثی باعث جریان جریان نمی شود. اگر شیب گونه های حامل بار صفر باشد، اصطلاح سمت چپ (جریان انتشار) نیز به دلیل خنثی بودن الکتریکی ناپدید می شود.
با این حال، حتی اگر اینطور نباشد، این اصطلاح اغلب بسیار کوچکتر از عبارت مرکزی (جریان مهاجرت) است، تا زمانی که غلظت یون های حامل جریان به طور قابل توجهی در محلول تغییر نکند. در شرایطی که ترکیب الکترولیت را می توان تقریباً ثابت در نظر گرفت و یون های حامل جریان به طور قابل توجهی تخلیه نمی شوند، می توان فرض کرد که جریان انتشار به میزان ناچیزی کمک می کند.
از این رو چنین نتیجه می شود که:
این عبارت برای چگالی جریان در رابط توزیع جریان ثانویه و همچنین رابط توزیع جریان اولیه استفاده می شود . تفاوت بین این رابط ها در درمان رابط های الکترود-الکترولیت است (به سینتیک واکنش های الکتروشیمیایی زیر مراجعه کنید). با توجه به موارد فوق، رسانایی الکترولیت σl به صورت زیر بدست می آید:
تا زمانی که این مقدار به طور قابل توجهی در محلول تغییر نکند، تقریب جریان انتشار صفر خوب است. اگر بتوان میزان انتشار و غلظت را ثابت در نظر گرفت، میتوانیم آن را تقریب کنیم:
مزیت بیان اهمی برای چگالی جریان این است که یک رابطه خطی از چگالی جریان به پتانسیل الکترولیت است. فقط در صورتی غیرخطی ضعیف است که σl مجاز باشد به غلظت حل شده در رابط حمل و نقل گونه بستگی داشته باشد . در مقایسه، معادلات نرنست-پلانک با خنثی الکتریکی میتواند بسیار غیرخطی باشد.
با این حال، تقریبهای مورد استفاده برای استخراج بیان توزیع جریان ثانویه، محدودیتهای سختتری را بر پیکربندیهای مجاز سیستم اعمال میکنند. قدرت یونی محلول باید تقریباً ثابت بماند تا تقریب رسانایی ثابت معتبر باشد. معمولاً این مورد فقط برای راه حل های رسانایی نسبتاً بالا است.
وقتی رسانایی نسبت به جریان کشیده شده زیاد باشد، میدان الکتریکی در محلول ناچیز می شود. برای میدانهای الکتریکی ناچیز، میتوان از تقریب فقط انتشار استفاده کرد که در آن E = 0 است . این معادلات نرنست-پلانک را به قوانین فیک تبدیل میکند و در صورت لزوم عبارتی برای انتقال همرفتی دارد. قوانین فیک با شرایط مرزی همرفت و الکتروشیمیایی در رابط الکتروآنالیز حل شده است .
حتی اگر فکر میکنید که مشکلی معادلات کامل نرنست-پلانک را شامل میشود، بهتر است ابتدا مدل را در توزیع جریان ثانویه تنظیم کنید تا ضمن استفاده از یک مدل الکتروشیمیایی سادهتر، هرگونه عارضه احتمالی دیگر در سیستم را شناسایی کنید. |
نظریه برای رابط های توزیع فعلی |




