گره Poroacoustics چندین مدل سیال را برای مدلسازی انتشار امواج صوتی در مواد متخلخل معرفی میکند. پس از چند نکته کلی در مورد مدل های سیال و تقریب های رژیم صلب و سست، این مدل ها در این بخش مورد بحث قرار می گیرند:
• | مدل های سیال متخلخل |
• | دلانی-بازلی-میکی |
• | هزینه های Zwikker |
• | آتنبورو |
• | ویلسون |
• | جانسون شامپو آلارد (JCA) |
• | جانسون شامپو آلارد لافارژ (JCAL) |
• | جانسون-شامپو-الارد-پراید-لافارژ (JCAPL) |
• | ویلیامز EDFM (مدل سیال چگالی معادل) |
• | چوب (مدل تعلیق مایع) |
مدل های سیال متخلخل
مدلهای سیال متخلخل، مدلهای سیال معادلی هستند که رفتارهای یک مدل مواد Poroelastic کامل را تقلید میکنند که توسط نظریه Biot تعریف شده است. یک مدل سیال متخلخل مبتنی بر توصیف چگالی سیال موثر وابسته به فرکانس ρ ( ω ) و مدول فله سیال موثر K ( ω ) سیستم معادل ترکیبی سیال-جامد (سیال اشباع و ماتریس متخلخل) است. شرح این مدل ها شامل تلفات مربوط به انتشار امواج صوتی در مواد متخلخل است. یک مدل سیال معادلاز نظر محاسباتی نسبت به مدل متخلخل کامل تقاضای کمتری دارد. با این حال، فقط از نظر فیزیکی برای انتخاب های خاصی از پارامترهای مواد صحیح است. بیشتر مدلهای متخلخل فقط در تقریبهای ماتریس متخلخل صلب یا سست معتبر هستند.
مدل های ماتریس متخلخل لیم و صلب
در حد ماتریس متخلخل صلب ، ماتریس آنقدر سفت فرض میشود که حرکت نمیکند (گاهی اوقات به عنوان مدل اسکلت بدون حرکت نامیده میشود ). در این مورد فرض می شود که در نظریه بیوت u = 0 ، که معادله موجی با چگالی مختلط و مدول حجمی را به دست می دهد. در یک ماده متخلخل صلب، ضریب Biot-Willis برابر با تخلخل α B = ε P است . همه مدلهای سیال متخلخل بر اساس تعریف دکل ρ چگالی مؤثر صلب هستند (رجوع کنید به شماره 9 ).
حد ماتریس متخلخل شل برعکس فرض صلب است. از آن برای مدلسازی موادی استفاده میشود که سفتی فازهای جامد (ماتریس متخلخل) آنقدر ضعیف است که نمیتواند از انتشار موج آزاد و ساختاری (نه طولی و نه عرضی) پشتیبانی کند. یعنی سفتی (در سختی توده ای در خلاء) در مقایسه با هوا بسیار کم است به طوری که حرکت فاز جامد از نظر صوتی قابل توجه می شود. اگر به اندازه کافی سبک باشد، فاز جامد همچنان حرکت می کند، زیرا توسط حرکت سیال “کشیده می شود”. یک مدل مواد متخلخل لنگی نیز یک مدل سیال معادل است زیرا فقط یک نوع موج طولی دارد. به طور معمول، فرض لنگی را می توان برای مواد فیبری با وزن بسیار سبک (کمتر از 10 کیلوگرم بر متر مکعب) اعمال کرد .) اگر با تزریق مواد چسبنده سفت نشدند. در حالت لنگی، فرض بر این است که تانسور تنش ناپدید میشود و در نظریه Biot، ضریب Biot-Willis α B = 1 است .
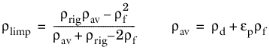
که ρ f چگالی سیال است، ρd چگالی ماتریس متخلخل تخلیه شده، ρ av میانگین چگالی موثر و ρ limp چگالی لنگی موثر حاصل است.
پارامترهای سیال
تعریف چگالی معادل و مدول حجمی منجر به سرعت معمول با مقادیر پیچیده صوت و چگالی (پارامترهای انتشار) می شود:
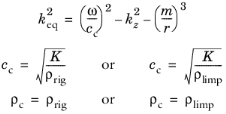
گزینه های گاز ایده آل و سیالات عمومی
ما در زیر نشان میدهیم که تمام مدلهای پیادهسازیشده آکوستیک متخلخل برای همه سیالات (گازها و مایعات) به جز مدل کاملاً تجربی دلانی-بازلی-میکی که از دادههای برازش تا اندازهگیری بهدست آمده است، اعمال میشود.
کاربرد مدلهای متخلخل آکوستیک برای سیالات عمومی در ادبیات توصیف نشده است، اما مستقیماً از تکرار مشتقات منتشر شده بدون فرض سیال اشباعکننده به عنوان یک گاز ایدهآل است. تنها تفاوت این است که باید از عبارت کلی زیر برای نسبت گرمای ویژه γ (بیان γ بر حسب سایر پارامترهای ماده) استفاده کرد که برای هر سیالی معتبر است (برای گازها γ معمولاً یک پارامتر شناخته شده است)
(2-43)  ،
،
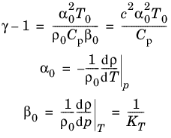 ،
،جایی که α 0 ضریب انبساط حرارتی ایزوباریک، T 0 دمای ساکن پس زمینه، ρ 0 چگالی ساکن پس زمینه، Cp گرمای ویژه در فشار ثابت، β 0 تراکم پذیری همدما (مدول توده ای همدما معکوس KT ) است . و c سرعت صوت است. این نتیجه از ترمودینامیک حاصل می شود.
برای نشان دادن کاربرد کلی مدلهای متخلخل، ما در اینجا مدول حجمی معادل را برای سادهترین حالت مدل Zwikker-Kosten برای یک سیال عمومی بازیابی میکنیم. تمام مدلهای پیادهسازیشده دیگر (دوباره به جز مدل دلانی-بازلی-میکی) پسوند این نتیجه هستند (نگاه کنید به رفر .
(2-44)
برای هر یک از این مدل ها، که در آن پاسخ فرکانسی Ψ ( ω ) برای هر مدل خاص است. در نتیجه، اشتقاق زیر برای نشان دادن نتیجه کلی کافی است.
استخراج مدول حجمی معادل برای هر سیال در نظریه Zwikker-Kosten
به طور کلی، مدول حجیم (ایسنتروپیک) توسط
(2-45)  .
.
یک رابطه بین فشار p و چگالی ρ برای تعریف مدول توده موثر مورد نیاز است و معادله حالت چنین رابطه ای را فراهم می کند. به جای تکیه بر معادله گاز ایده آل، در اینجا از معادله کلی حالت زیر استفاده می کنیم
(2-46)
که صرفاً تصریح می کند که چگالی ρ تابعی از فشار p و دمای T است . وابستگی به دما غیر قابل چشم پوشی است زیرا ما با منافذ کوچک سروکار داریم و آکوستیک در مواد متخلخل به آکوستیک ترموویسکوز تعلق دارد (به رابط های صوتی ترموویسکوز مراجعه کنید ). با فرض اینکه میدانهای صوتی، اغتشاشات هارمونیک کوچکی هستند (که با زیرنویس 1 مشخص میشوند) در مورد یک حالت مرجع ساکن (که با زیرنویس 0 مشخص میشود)
(2-47)
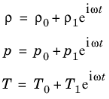
و تیلور با گسترش معادله عمومی حالت معادله 2-46 به مرتبه اول، متوجه می شویم
(2-48)
که β T تراکم پذیری همدما است.
به منظور محاسبه مدول توده موثر از معادله 2-45 با استفاده از معادله حالت معادله 2-48 ، یک رابطه بین T 1 و p 1 از معادله انرژی خطی گرفته شده است (به پیشینه تئوری برای شاخه آکوستیک ترموویسکوز مراجعه کنید ).
(2-49)
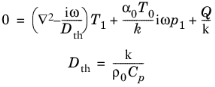
که در آن D th انتشار حرارتی، k هدایت حرارتی، و Q یک منبع حرارتی حجمی است. برای ادامه حل این معادله، به طور کلی فرض می شود که ( i ) منفذ را می توان به عنوان یک استوانه توخالی مدل کرد، ( ii ) سهم تغییرات شعاعی بر تغییرات محوری غالب است، بنابراین برای حل مسئله شعاعی کافی است در حالی که فرض نمی کنیم تغییرات محوری Ref. 9 ، و ( iii ) شعاع منافذ بسیار کوچکتر از طول موج است، به طوری که فشار در سراسر شعاع تغییر محسوسی نمی کند. با این مفروضات فشار p 1 را می توان به عنوان یک ثابت در در نظر گرفتمعادله 2-49 و معادله فقط تغییرات شعاعی دارد:
میانگین محلول مقطعی تحت این مفروضات، و با شرایط مرزی دمای آکوستیک صفر T 1 بر روی دیواره های منافذ در r = R، است .
(2-50)  .
.
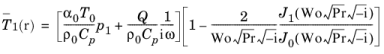 .
.اینجا
(2-51)
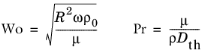
که در آن Wo عدد وومرسلی است (به یادداشت زیر مراجعه کنید)، و Pr عدد پراندتل است، که عرض نسبی ضخامت لایه مرزی چسبناک را به ضخامت لایه مرزی حرارتی اندازه میگیرد.
با حل معادله 2-50 ، فشار را می توان به عنوان تابعی از چگالی با استفاده از معادله مرتبه اول حالت معادله 2-48 بیان کرد :
(2-52)
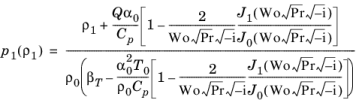
از این عبارت عبارت زیر را برای مدول حجمی معادل به دست می آوریم (به معادله 2-45 مراجعه کنید )
(2-53)
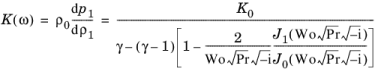
که در آن نسبت گرمای ویژه γ در معادله 2-43 برای یک سیال عمومی تعریف شده است و K 0 مدول حجمی ایزنتروپیک سیال است. این فرمول معادله 2-53 از نظر ریاضی معادل با فرمول معمولی Zwikker-Kosten برای مدول حجمی معادل است (نگاه کنید به مرجع 15 )، اما برای یک سیال عمومی و نه فقط یک گاز ایده آل مشتق شده است .
ما تأکید می کنیم که از این نتیجه برای یک سیال عمومی از فرمول کلی معادله 2-44 پیروی می کند ، در این مورد خاص با
(2-54)
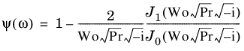
با عدد وومرسلی Wo حاوی وابستگی فرکانس.
عدد Womersley تاثیر اثرات چسبناک را نسبت به فرکانس نوسان ω اندازه گیری می کند . برای |
دلانی-بازلی-میکی
مدل Delany-Bazley-Miki یک مدل سیال معادل است که تلفات عمده در مواد متخلخل/فیبری خاص را تقلید می کند. مدل یک محیط متخلخل با ثابت های انتشار پیچیده زیر را نشان می دهد:
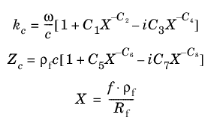
که ρ f چگالی سیال، f فرکانس و Rf مقاومت جریان است. چندین مجموعه از پیش تعریف شده از ضرایب C i وجود دارد. آنها مدل کلاسیک Delany-Bazley، مدل Miki (نگاه کنید به مرجع 9 ، بخش 2.5 و مرجع 22 )، Qunli، چندین گونه از مدل Mechel برای پیکربندی های مختلف، مدل Komatsu، و به اصطلاح Champoux اصلاح شده هستند. و مدل Allard (نگاه کنید به مرجع 23 ). اینها همگی مدلهای تجربی هستند که بر اساس برازش دو تابع پیچیده با دادههای اندازهگیری شده برای عدد موج مختلط kc و امپدانس صوتی خاص پیچیده Zc هستند.. همه مدل ها برای موادی با تخلخل ε p نزدیک به 1 قابل استفاده هستند. کاربرد پارامترهای مدل مختلف در جدول 2-10 و همچنین Ref. 23 برای جزئیات بیشتر
نام مدل | قابلیت کاربرد |
دلانی-بازلی | پشم شیشه و سنگ با: 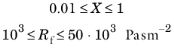 |
میکی | پشم شیشه و سنگ با: 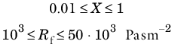 اعتبار مدل با استفاده از پارامترهای Miki برای X < 0.01 به خوبی تثبیت نشده است ، اما این مدل با استفاده از پارامترهای Miki به جای پارامترهای Delany-Bazley از نظر ریاضی در زیر این حد کمی بهتر رفتار می کند . 22 . |
کونلی | پلاستیک متخلخل و فوم های باز: 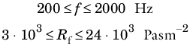 |
Mechel، الیاف شیشه، کم X | الیاف شیشه: |
Mechel، الیاف شیشه، X بالا | الیاف شیشه: |
Mechel، فیبر سنگ، کم X | الیاف سنگ: |
Mechel، فیبر سنگ، X بالا | الیاف سنگ: |
کوماتسو | پشم شیشه و سنگ: |
Champoux و Allard اصلاح شده |
هزینه های ZWIKKER
Zwikker-Kosten یکی از اولین مدل های سیال معادل برای مواد متخلخل است ( مراجعه 15 ). این یک مدل قاب صلب است که با چگالی پیچیده (صلب) تعریف می شود
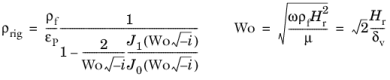
که در آن H r شعاع هیدرولیکی منافذ است (برای منافذ استوانه ای مستقیم H r = a = شعاع) و Wo عدد وومرزلی است (به معادله 2-51 و یادداشت زیر مراجعه کنید). Wo مربوط به نسبت بین عمق نفوذ ویسکوز δv و شعاع هیدرولیکی است. δ v مقیاس ضخامت لایه مرزی چسبناک را نشان می دهد ( برای جزئیات به پیشینه تئوری برای شاخه آکوستیک ترموویسکوز مراجعه کنید ). مدول حجمی توسط
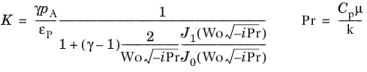
که در آن p A فشار محیط، ρf چگالی سیال، γ نسبت گرمای ویژه، Pr عدد پراندتل، μ ویسکوزیته دینامیکی، Cp ظرفیت گرمایی در فشار ثابت، و k ضریب هدایت حرارتی را نشان میدهد . J 0 و J 1 توابع بسل از نوع اول هستند. فاکتور γ p A مدول توده همسانتروپیک است ( K 0 = γ p A ). پارامترهای آزاد منافذ تخلخل ε P است و شعاع هیدرولیک Hr .
آتنبورو
مدل Attenborough نیز بر اساس فرض منافذ استوانهای شکل است. این یک مدل به اصطلاح نیمه تجربی چهار پارامتری است. این مدل توسعه ای از مدل Zwikker-Kosten است و دو پارامتر ورودی دیگر را اضافه می کند. پیچ خوردگی (محدودیت فرکانس بالا) τ∞ را به حساب می آورد که به جهت منافذ نسبت به جهت انتشار مربوط می شود. قطر هیدرولیکی منافذ با عبارتی جایگزین میشود که شامل مقاومت جریان Rf و پارامتر برازش b است (این پارامتر مربوط به ناهمسانگردی منافذ است). رجوع کنید به رفر. 9 و رفر. 16 . چگالی معادل و مدول حجمی به صورت تعریف شده است
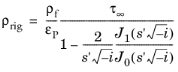
و
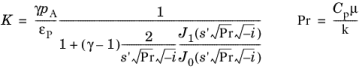
که در آن p A فشار محیط، ρf چگالی سیال، γ نسبت گرمای ویژه، Pr عدد پراندتل، μ ویسکوزیته دینامیکی، Cp ظرفیت گرمایی در فشار ثابت، و k ضریب هدایت حرارتی را نشان میدهد . J 0 و J 1 توابع بسل از نوع اول هستند. متغیر s (عامل ناهمسانگردی) از سایر پارامترهای ماده مشتق شده و به عدد وومرسلی مربوط می شود (به معادله 2-51 مراجعه کنید ) :
در اینجا ω فرکانس زاویه ای را نشان می دهد. چهار پارامتر مورد نیاز (زمانی که سیال در دمای اتاق هوا باشد) عبارتند از تخلخل εP ، پیچ خوردگی τ∞ ، مقاومت جریان Rf ، و پارامتر اتصال b ( بدون ابعاد، نزدیک به 1). پارامتر برازش b برای برخی از مقاطع عرضی منفذی به خوبی تعریف شده در جدول 2-11 ارائه شده است .
شکل مقطع | ب |
دایره | 1 |
مربع | 1.07 |
مثلث متساوی الاضلاع | 1.11 |
شکاف مستطیلی | 0.81 |
به این ترتیب، شعاع هیدرولیکی مدل Attenborough از نظر خواص ذاتی قابل اندازه گیری مواد متخلخل فرموله می شود که نیاز به دانستن شعاع منافذ را کاهش می دهد.
طول مشخصه چسبناک مدل L v را نیز می توان با تعریف کرد
با δ v عمق نفوذ چسبناک. این طول مربوط به شعاع مقطع دایره ای منافذ R (برای یک استوانه) و ضخامت لایه مرزی چسبناک است. پارامتر b = 1/ s که s پارامتر طول مشخصه ویسکوز است. مدل های زیر را ببینید:
• | جانسون شامپو آلارد (JCA) |
• | جانسون شامپو آلارد لافارژ (JCAL) |
• | جانسون-شامپو-الارد-پراید-لافارژ (JCAPL) ). |
توجه داشته باشید که پیچ خوردگی به زاویه θ بین منافذ استوانه ای و جهت انتشار موج مربوط می شود.
ویلسون
مدل ویلسون تعمیم مدل های تحلیلی برای مواد متخلخل با سطح مقطع ثابت و منافذ موازی است. این مدل برای مطابقت با رفتار فرکانس میانی یک ماده متخلخل در نظر گرفته شده است (رجوع کنید به مرجع 9 ، مرجع 17 ، و مرجع 18 ). برای ω که به 0 یا بی نهایت تمایل دارد، مدل خوبی نیست . چگالی معادل و مدول حجمی با استفاده از
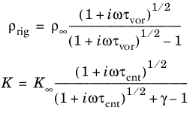
که در آن τ vor زمان آرامش حالت گردابی را نشان میدهد، τ زمان آرامش حالت آنتروپی، ρ∞ حد بینهایت فرکانس برای چگالی، K∞ حد بینهایت فرکانس برای مدول حجمی، و γ نسبت خاص است . گرم می کند. این چهار پارامتر رایگان هستند. با انتخاب های مناسب برای پارامترهای آرامش، مدل ویلسون را می توان برای تقلید از همه مدل های شرح داده شده در اینجا نصب کرد. به عنوان مثال، تنظیم τ vor = 2.54 / R f و τ ent = 3.75 / R f، معادلات از مدل دلانی-بازلی تقلید می کنند (به Cox and D’Antonio Sec. 5.4.4، Ref. 18 مراجعه کنید ).
عبارات تقریبی بر اساس پارامترهای غیر آکوستیک (خواص ماتریس متخلخل) نیز برای زمان های آرامش وجود دارد:
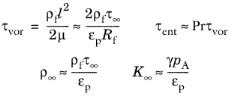
در اینجا τ ∞ نشاندهنده پیچخوردگی (محدودیت فرکانس بالا) است (که در مقاله ویلسون به آن q 2 گفته میشود ) ، ε p تخلخل ، ρf چگالی سیال ، l یک بعد منافذ مشخصه، و Pr عدد پراندتل است. .
جانسون شامپو آلارد (JCA)
مدل ماتریس متخلخل جانسون-شامپوکس-آلارد (JCA) با چگالی صلب معادل ρ rig ( ω ) و مدول توده معادل K ( ω ) تعریف میشود:
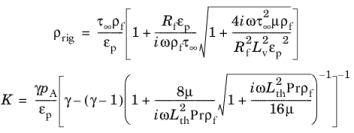
در اینجا τ ∞ ضریب پیچ خوردگی (حد فرکانس بالا)، ρ f چگالی سیال، ε p تخلخل، R f مقاومت جریان، μ ویسکوزیته دینامیکی، p A فشار ساکن، γ است. نسبت گرمای ویژه، Lv طول مشخصه چسبناک، L th طول مشخصه حرارتی، و Pr عدد پراندتل است . طول مشخصه ویسکوز با پارامتر طول مشخصه چسبناک s در ارتباط است
در اینجا s یک فاکتور وابسته به هندسه منافذ بین 0.3 و 3.0 است (به عنوان مثال 1 برای منافذ دایره ای، 0.78 برای شکاف ها)
عبارت داده شده برای عامل منافذ وابسته به هندسه s فقط برای مقادیر s نزدیک به 1 معتبر است. اگر اینطور نیست، طول مشخصه چسبناک Lv را مستقیماً در مدل وارد کنید (انتخاب پیش فرض). |
طول مشخصه چسبناک Lv و L th حرارتی نیز گاهی اوقات به ترتیب با Λ و Λ ‘ نشان داده می شود . |
جاذب متخلخل : مسیر کتابخانه کاربردی Acoustics_Module/Building_and_Room_Acoustics/porous_absorber |
جانسون شامپو آلارد لافارژ (JCAL)
مدل Johnson-Champoux-Allard-Lafarge (JCAL) اصلاحاتی را در رفتار حرارتی مدول حجیم در فرکانسهای پایین ارائه میکند که توسط مدل JCA ثبت نشده است (رجوع کنید به شماره 13 ). چگالی معادل مانند مدل JCA است. تصحیح به مدول حجیم است و توسط داده می شود
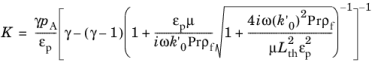
با معرفی پارامتر جدید، k’ 0 ، که نفوذپذیری حرارتی استاتیکی است (واحد SI: m 2 ). برای اندازه گیری ها و جزئیات این پارامتر رجوع کنید . 11 و رفر. 12 برای مثال
جانسون-شامپو-الارد-پراید-لافارژ (JCAPL)
مدل Johnson-Champoux-Allard-Pride-Lafarge ( JCAPL) مدلهای JCAL را با معرفی ت 0 ویسکوز استاتیک و پیچخوردگی τ’0 حرارتی ، که هر دو اصلاحات فرکانس پایین را به مدلهای JCAL و JCA ارائه میکنند، بیشتر گسترش میدهد. رجوع کنید به رفر. 14 و ر. 9 .
این مدل دارای چگالی صلب پیچیده است که توسط:
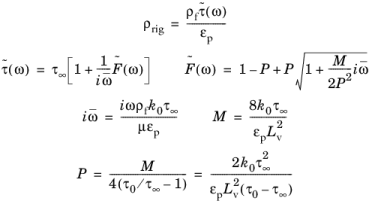
که در آن پارامتر جدید پیچش چسبناک استاتیک τ 0 (بدون بعد) است. نفوذپذیری چسبناک به صورت k 0 = μ/ R f (واحد SI: m2 ) تعریف می شود.
در Ref. 9 (معادله 5.32)، P را b ، k 0 را q 0 و Pr را B 2 می نامند . |
مدول حجمی مختلط K توسط:
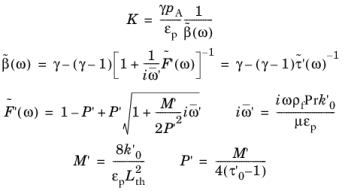
که در آن پارامتر جدید پیچش حرارتی استاتیک τ ‘ 0 (بدون بعد) است.
در Ref. 9 (معادله 5.35)، α ‘ ( ω |
مدل JCA با تنظیم M ‘ = P = P ‘ = 1 و JCAL با تنظیم P = P ‘ = 1 بازیابی می شود . |
ویلیامز EDFM (مدل سیال چگالی معادل)
مدل ویلیامز EDFM یک مدل سیال با چگالی معادل است. این مدل با این فرض به دست میآید که مدولهای حجیم و برشی قاب مواد متخلخل ناچیز هستند، رجوع کنید به Ref. 24 برای جزئیات بیشتر به همین دلیل است که مدل مربوط به رسوبات است. مدول حجیم مؤثر K eff و چگالی مؤثر ρ eff که مدل من را تعریف میکند توسط داده میشود
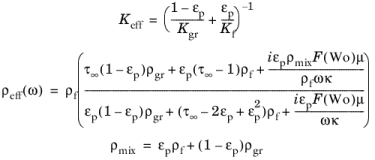
که در آن زیرنویس “gr” مربوط به دانه ها و علامت “f” به مایع اشباع کننده مربوط می شود. تخلخل ε p ، چگالی مخلوط مشاهده شده ρ مخلوط ، پیچ خوردگی  ، ویسکوزیته دینامیکی μ ، فرکانس زاویه ای ω ، و نفوذپذیری رسوبات κ نشان داده می شود . تابع F تابعی از عدد Womersley است که به صورت تعریف شده است
، ویسکوزیته دینامیکی μ ، فرکانس زاویه ای ω ، و نفوذپذیری رسوبات κ نشان داده می شود . تابع F تابعی از عدد Womersley است که به صورت تعریف شده است
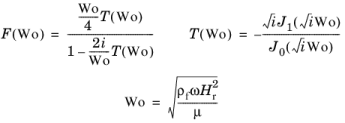
که در آن J n ( x ) تابع بسل از نوع اول مرتبه n و H r شعاع هیدرولیکی است. بر این اساس سرعت پیچیده موثر صوت و چگالی به صورت داده شده است
چوب (مدل تعلیق مایع)
در یک مخلوط سیال یا یک سوسپانسیون سیال (قطعات جامد کاملاً توسط سیال احاطه شده است) می توان از فرمول Wood برای تعیین سرعت موثر صدا برای مخلوط استفاده کرد. با محاسبه مدول حجیم موثر تعلیق و چگالی متوسط حجمی تعیین می شود. به عنوان EDFM ویلیامز، این مدل مقادیر موثری را برای مخلوط ارائه می دهد. این نتیجه برای فرکانس های پایین دقیق است (زمانی که طول موج بسیار بزرگتر از اندازه اجزاء باشد) زیرا مدول توده موثر در حد شبه استاتیک است. مدل Wood تعریف می کند
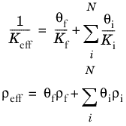
که در آن θf ، Kf ، و ρf ، به ترتیب کسر حجمی، مدول حجمی آدیاباتیک و چگالی سیال هستند . و θi ، Ki ، و ρi ، به ترتیب کسرهای حجمی، مدولهای حجیم آدیاباتیک و چگالی هستند . و دوباره سرعت پیچیده صوت و چگالی به صورت تعریف شده است




