مدلهای سیال آکوستیک منطقه باریک برای تقلید تلفات حرارتی و چسبناکی که در لولههای باریک وجود دارد، استفاده میشود که در آن مقیاس طول مقطع لوله با ضخامت لایه مرزی حرارتی و چسبناک (جذب لایه مرزی) قابل مقایسه است. برای به دست آوردن نتایج صحیح، گنجاندن این ضررها ضروری است.
این مدلها معمولاً در موقعیتهایی استفاده میشوند که حل یک مدل آکوستیک ترموویسکوز با جزئیات کامل از نظر محاسباتی پرهزینه است. به عنوان مثال هنگام تجزیه و تحلیل مجاری/لوله های باریک بلند با سطح مقطع ثابت. در اینجا می توان تلفات مربوط به لایه مرزی را به قسمت عمده سیال اضافه کرد یا آغشته کرد: یک مدل سیال معادل. برای بسیاری از هندسه ها، عبارات تحلیلی برای تلفات مرتبط با لایه های مرزی آکوستیک وجود دارد. مدل ها را می توان تحت مفروضات مختلف اعمال کرد. مدل ها و مفروضات در این بخش مورد بحث قرار می گیرند.
در هندسههای پیچیدهتر که تلفات حرارتی و ویسکوزیته مهم هستند، به Thermoviscous Acoustics، Frequency Domain Interface مراجعه کنید ، که اساسیتر و دقیقتر است. |
آکوستیک منطقه باریک |
چندین مدل مایع وجود دارد:
• | تقریب مجرای عریض را می توان برای هر مقطع مجرای در محدوده ای که عرض مجرا به طور قابل توجهی بزرگتر از ضخامت لایه مرزی صوتی باشد، استفاده کرد. کانال های عریض را ببینید . |
• | مجرای دایره ای بسیار باریک (همدما) را فقط زمانی می توان استفاده کرد که عرض مجرا آنقدر کم باشد که شرایط همدما اعمال شود. این زمانی است که عرض کانال بسیار کوچکتر از ضخامت لایه مرزی حرارتی صوتی است. مجاری دایره ای بسیار باریک (همدما) را ببینید . |
• | مدلهای شکاف ، مجرای دایرهای ، مجرای مستطیلی و مجرای مثلثی متساوی الاضلاع مبتنی بر حل تحلیلی معادلات صوتی ترموویسکوز در حدی هستند که در آن طول موج صوتی بسیار بزرگتر از سطح مقطع مجرا (زیر فرکانس قطع) و مرز است . ضخامت لایه. این مورد در بیشتر کاربردهای مهندسی است. به شکاف ها، مجراهای دایره ای، مجرای مستطیلی و مجاری مثلثی متساوی الاضلاع مراجعه کنید . |
• | در نهایت، انتخاب گزینه تعریف شده توسط کاربر شما را قادر می سازد تا عباراتی را برای عدد موج مختلط و امپدانس صوتی پیچیده وارد کنید. اینها ممکن است عبارات تحلیلی، مقادیر درون یابی، یا مقادیر استخراج شده از تجزیه و تحلیل حالت مرزی دقیق با استفاده از فرمول کامل Thermoviscous Acoustics، Boundary Mode Interface باشند . |
کانال های عریض
برای یک مجرای نسبتاً گسترده، تلفات وارد شده در لایه مرزی آکوستیک ممکن است با افزودن آنها به عنوان یک نیروی برشی موثر دیوار مورد مطالعه قرار گیرد. این رویکرد در Blackstock استفاده می شود ( مرجع 6 ) و منجر به معادل موج مختلط سیال عدد k c تعریف شده توسط
(2-55)
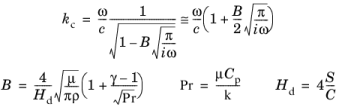
که در آن Hd قطر هیدرولیکی مجرا، S سطح مقطع مجرا، C محیط مجرا، μ ویسکوزیته دینامیکی، ρ چگالی سیال، γ نسبت گرمای ویژه، C p است. گرمای ویژه در فشار ثابت، k هدایت حرارتی سیال و Pr عدد پراندتل است. برای یک مجرای استوانه ای، Hd = 2a که در آن a شعاع است.
تقریب در معادله 2-55 فقط برای سیستم هایی معتبر است که شعاع موثر Hd /2 بزرگتر از لایه مرزی است، اما نه آنقدر کوچک که تلفات حرارتی و چسبناک جریان اصلی مهم باشد. بنابراین نیاز است
جایی که δ v ضخامت مشخصه لایه مرزی چسبناک (عمق نفوذ چسبناک)، c سرعت صوت و ω فرکانس زاویه ای است. عدد موج مختلط با چگالی و سرعت مختلط صوت توسط معادله (با فرض یک مدول حجمی واقعی) مرتبط است.
مجاری دایره ای بسیار باریک (همدما)
در حد دیگر که در آن قطر مجرا به اندازه کافی کوچک یا فرکانس به اندازه کافی کم است، ضخامت لایه مرزی حرارتی بسیار بزرگتر از سطح مقطع کانال a می شود . این مورد زمانی است که
که در آن δ th ضخامت مشخصه لایه مرزی حرارتی (عمق نفوذ حرارتی)، ρ چگالی، Cp ظرفیت گرمایی در فشار ثابت، و k هدایت حرارتی سیال است. در این مورد پیرس ( مراجعه 5 ) را ببینید. سیستم ممکن است به صورت همدما دیده شود و تغییرات دمای صوتی در همه جای مجرا صفر است T = 0. سپس موج مختلط سیال عدد kc با تعریف می شود.
(2-56)
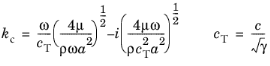
که در آن c T سرعت همدما صوت، a شعاع مجرا، μ ویسکوزیته دینامیکی و ω فرکانس زاویه ای است. این تئوری برای کانال های مقطع دایره ای مشتق شده است – بنابراین این مدل فقط برای سیستم هایی با تغییرات کوچک دور از مقطع دایره ای قابل استفاده است. عدد موج مختلط به چگالی و سرعت مختلط صوت توسط معادله مربوط می شود (در اینجا مدول حجمی در حد همدما تعریف می شود)
شکاف ها، مجرای دایره ای، مجرای مستطیلی و مجاری مثلثی متساوی الاضلاع
مدل های شکاف، مجرای دایره ای، مجرای مستطیلی و مجرای مثلثی متساوی الاضلاع بر اساس مدل به اصطلاح فرکانس کاهش یافته کم (LRF) هستند که انتشار امواج صوتی را در موجبرهای کوچک (مجرای و شکاف ها) از جمله تلفات حرارتی و چسبناک توصیف می کند. جزئیات این مدل ها در Ref. 19 ، ر. 20 و رفر. 21 . مدلها محدودهای از شرایط کاملاً همدما (فرکانسهای بسیار کم یا لولههای بسیار باریک) تا کانالهای بزرگ را پوشش میدهند که در آن لایه مرزی تنها کسری از اندازه مجرا را نشان میدهد. این مدلها تا زمانی اعمال میشوند که سطح مقطع مجرا بسیار کوچکتر از طول موج صوتی باشد (مدل زیر فرکانس قطع است) و زمانی که سطح مقطع ثابت است یا بسیار آهسته تغییر میکند.
در یک موجبر باریک، عدد موج مختلط، kc ، و امپدانس صوتی خاص پیچیده، Zc ، با
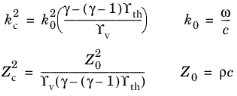
که Υ v و Υ th به ترتیب مقدار میانگین (میانگین مقطع) توابع ویسکوز اسکالر و میدان حرارتی هستند. توابع هندسه و توابع وابسته به مواد هستند (در زیر مشخص شده است) و γ نسبت گرمای ویژه است. چگالی سیال ρ ، سرعت صوت c است و فرکانس زاویه ای ω عدد موج فضای آزاد k 0 و امپدانس صوتی خاص Z 0 را مشخص می کند . زیرنویس های ” v ” و “th”به ترتیب مخفف میدان چسبناک و گرمایی (گرمایی) است. هنگامی که اینها شناخته شدند، سرعت مختلط صوت و چگالی مختلط بر اساس داده می شود
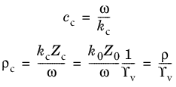
مقادیر توابع Υj را می توان با حل مجموعه کامل معادلات خطی شده ناویر-استوکس (معادلات حل شده توسط رابط های صوتی ترموویسکوس، به پیشینه تئوری برای شاخه آکوستیک ترموویسکوز مراجعه کنید ) با تقسیم این معادلات به یک ایزنتروپیک (آدیاباتیک) به دست آورد. یک بخش چسبناک و یک بخش حرارتی. انجام این کار اعداد ویسکوز و موج حرارتی را برای سیستم معرفی می کند
معادلات را می توان به صورت تحلیلی تحت مفروضات زیر که برای مدل های LRF استفاده می شود حل کرد:
• | اعداد موج چسبناک و حرارتی باید بسیار بزرگتر از عدد موج صوتی باشد (طول موج صوتی باید بسیار بزرگتر از ضخامت لایه مرزی باشد): |
• | سطح مقطع موجبر باید بسیار کوچکتر از طول موج صوتی باشد (مدل زیر فرکانس قطع است). |
• | سطح مقطع موجبر باید ثابت باشد یا حداکثر در جهت انتشار به آرامی تغییر کند. |
• | طول موجبر در جهت انتشار باید بزرگتر از ضخامت لایه مرزی باشد. |
عبارات تحلیلی حاصل، برای توابع Υ چسبناک و حرارتی ، برای هندسه داده شده هستند (این نتایج در کد 19 بررسی شده است ):
• | شکاف ارتفاع h |
• | مجرای دایره ای به شعاع a |
• | مجرای مستطیلی با طول ضلع W و H |
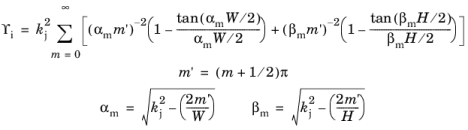
• | مجرای مثلثی متساوی الاضلاع به طول ضلع d |
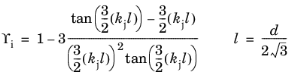
تعریف شده توسط کاربر
گزینه تعریف شده توسط کاربر در ویژگی دامنه آکوستیک منطقه باریک می تواند برای تعریف یک مدل LRF برای یک موجبر از یک مقطع دلخواه استفاده شود. مقادیر موج مختلط عدد kc و امپدانس مختلط مشخصه Z c را وارد کنید . این می تواند یک عبارت تحلیلی تعریف شده توسط کاربر یا مقادیری باشد که از یک مطالعه تحلیل حالت به دست آمده است.
برای تعیین ثابت های انتشار پیچیده برای یک موجبر، با مقطع دلخواه، از Thermoviscous Acoustics، Boundary Mode Interface استفاده کنید . آن را روی هندسه مقطع موجبر اعمال کنید. رابط حالت های انتشار را حل می کند و تمام تلفات را با جزئیات در بر می گیرد. سپس عدد موج مختلط kc توسط حالت موج صفحه حل شده برای آن داده می شود . این متغیر tabm.kn است . متغیر از پیش تعریف شده tabm.Zc امپدانس مشخصه پیچیده (مجموعه) Z c را می دهد . نزدیکترین حالت به حالت موج هواپیما (بدون ضرر) را جستجو کنید. |




