درباره حل کننده وابسته به زمان

اطلاعات پیش‌زمینه زیر در مورد حل‌کننده وابسته به زمان این موضوعات را مورد بحث قرار می‌دهد: الگوریتم‌های حل وابسته به زمان ضمنی و BDF در مقابل روش‌های عام آلفا و صریح . همچنین به انتخاب یک حل کننده ثابت، وابسته به زمان یا مقدار ویژه مراجعه کنید .


	زمان در کتابچه راهنمای مرجع برنامه نویسی مولتیفیزیک COMSOL .

الگوریتم های حل کننده ضمنی وابسته به زمان

گسسته سازی المان محدود مسئله PDE وابسته به زمان است

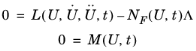
که اغلب از آن به عنوان روش خطوط یاد می شود . قبل از حل این سیستم، الگوریتم ضریب لاگرانژ Λ را حذف می کند . اگر قیود 0 = M خطی و مستقل از زمان باشند و اگر نیروی محدودیت Jacobian N F ثابت باشد، الگوریتم محدودیت‌ها را نیز از سیستم حذف می‌کند. در غیر این صورت، محدودیت ها را حفظ می کند و منجر به یک سیستم تفاضلی-جبری می شود.

در COMSOL Multiphysics، حل کننده های IDA و generalized-a برای حل سیستم ODE یا DAE فوق در دسترس هستند:

•

IDA در آزمایشگاه ملی لارنس لیورمور ( مرجع 4 ) ایجاد شد و یک پیاده‌سازی مدرن از حل‌کننده DAE DASPK ( مرجع 5 ) است که از فرمول‌های تمایز به عقب اندازه متغیر مرتبه متغیر (BDF) استفاده می‌کند. به صورت اختیاری، یک کنترل‌کننده غیرخطی می‌تواند کنترل دقیق‌تری از گام‌های زمانی ارائه دهد، که می‌تواند ضربات گام‌های زمانی را کاهش دهد که به عنوان مثال، تعداد مراحل زمانی را افزایش می‌دهد و عملکرد را برای مسائل بسیار غیرخطی در CFD کاهش می‌دهد. رجوع کنید به رفر. 7 برای اطلاعات بیشتر در مورد کنترل کننده غیر خطی (کنترل کننده STAB).

•

تعمیم یافته- α یک روش دقیق ضمنی و مرتبه دوم با پارامتر α یا ρ∞ ( 0 ≤ ρ ∞ ≤ 1 ) برای کنترل میرایی فرکانس های بالا است . با ρ ∞ = 1 ، روش میرایی عددی ندارد. برای مسائل خطی، این با قانون نقطه میانی مطابقت دارد. ρ ∞ = 0 حداکثر میرایی عددی را نشان می دهد. برای مسائل خطی بالاترین فرکانس در یک مرحله از بین می رود. این روش ابتدا برای معادلات مرتبه دوم در مکانیک سازه توسعه یافت ( مرجع 10 ) و بعداً به سیستم های مرتبه اول گسترش یافت. مرجع. 11 ).

برای طرح های گام زمانی ضمنی، یک حل کننده غیرخطی برای به روز رسانی متغیرها در هر مرحله زمانی استفاده می شود. حل‌کننده غیرخطی مورد استفاده توسط زیرگره‌های حل‌کننده کاملاً جفت‌شده و جداشده کنترل می‌شود . این زیرگره‌ها کنترل زیادی بر فرآیند حل غیرخطی ارائه می‌کنند: می‌توان تلورانس غیرخطی، ضریب میرایی، تعداد دفعات به‌روزرسانی ژاکوبین و تنظیمات دیگری را انتخاب کرد که الگوریتم سیستم غیرخطی را کارآمدتر حل کند.

برای حل کننده BDF (IDAS) جایگزین دیگری وجود دارد و آن استفاده از حل کننده غیرخطی داخلی IDAS است. این حل کننده زمانی استفاده می شود که تمام گره های و غیر فعال باشند. حل کننده خطی در این حالت توسط زیرگره حل کننده خطی فعال کنترل می شود.

خطی سازی سیستم فوق که در تکرار نیوتن استفاده شده است

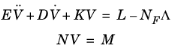
که در آن K = −∂ L /∂ U ماتریس سختی است،

ماتریس میرایی است و

ماتریس جرم است. هنگامی که E = 0 ، D اغلب ماتریس جرم نامیده می شود.

هنگام استفاده از IDA برای مسائل مربوط به مشتقات زمانی مرتبه دوم ( E ≠ 0 )، متغیرهای اضافی به صورت داخلی معرفی می شوند به طوری که امکان تشکیل یک سیستم مشتق زمانی مرتبه اول وجود دارد (این اتفاق در هنگام استفاده از α تعمیم داده نمی شود ، زیرا می تواند ادغام معادلات مرتبه دوم). بردار متغیرهای اضافی، در اینجا U v ، با معادله اضافی می آید

که در آن U بردار متغیرهای اصلی را نشان می دهد. این روش سیستم ODE یا DAE اصلی را گسترش می‌دهد تا اندازه اصلی خود را دو برابر کند، اما سیستم خطی شده با ماتریس E + σ D + σ 2 K به اندازه اصلی کاهش می‌یابد، که σ یک اسکالر به طور معکوس متناسب با گام زمانی است. با معادله اضافه شده، متغیر اصلی U همیشه یک متغیر دیفرانسیل است (شاخص-0). آزمون خطا متغیر U v را مستثنی می کند مگر اینکه مقداردهی اولیه ثابت روشن باشد، در این صورت متغیرهای دیفرانسیل U v در آزمون خطا گنجانده می شوند و استراتژی تخمین خطا برای جبری اعمال می شود.U v -متغیرها.

تنظیمات تحمل مطلق برای حل کننده وابسته به زمان

برای حل وابسته به زمان در بخش ، تحمل مطلق و نسبی خطا را در هر مرحله ادغام کنترل می کنند. به طور خاص، اجازه دهید U بردار حل مربوط به راه حل در یک مرحله زمانی خاص باشد، و اجازه دهید E تخمین حل کننده از خطای مطلق (محلی) در U باشد که در طول این مرحله زمانی انجام شده است. برای روش ، مرحله پذیرفته می شود اگر

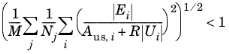
که در آن A us ,i تلورانس مطلق بدون مقیاس برای DOF i، R تلورانس نسبی، M تعداد فیلدها و N j تعداد درجات آزادی در میدان j است . اعداد A us ,i از تبدیل مقدار ورودی A k برای متغیر وابسته مربوطه k محاسبه می شوند . برای درجات آزادی برای توابع شکل لاگرانژ یا برای ODE ها، این مقادیر همان مقدار وارد شده است (یعنی A us ,i = A k)، اما برای عناصر برداری یک عامل تبدیل میدان به DOF وجود دارد.

برای روش و هنگامی که انتخاب می کنید ، مرحله پذیرفته می شود اگر

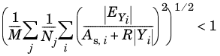
که در آن E Y تخمین حل کننده از خطای مطلق (محلی) در Y است ، A s، i تلورانس مطلق مقیاس شده برای DOF i است ، M تعداد فیلدها، R تحمل نسبی، N j تعداد درجه است. آزادی در میدان j و Y i بردار حل مقیاس شده است. برای متغیرهای وابسته که از روش مقیاس بندی استفاده می کنند ، اعداد A s ,i از مقادیر ورودی A k طبق فرمول محاسبه می شوند.

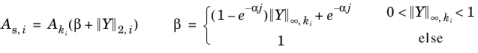
که در آن α = 1/5 ، j عدد تکرار مرحله زمانی j = 0،1،…، و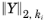

، به ترتیب

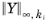هنجار 2 و حداکثر هنجار متغیر وابسته k i است . در اینجا

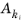مقدار ورودی تبدیل شده A k برای فیلد k و DOF i است. برای متغیرهای وابسته که از روش مقیاس‌بندی دیگری استفاده می‌کنند یا وقتی کادر تأیید پاک می‌شود، سپس

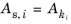توجه داشته باشید که با تنظیم روی ، تلورانس مطلق به عنوان ضریب تلورانس نسبی مشخص می شود. اگر به جای آن از یک تلورانس مطلق خاص استفاده کنید، آن مقدار می تواند اثر کاهش بیشتر تحمل نسبی را کاهش دهد (به طوری که وقتی،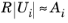

اثر کاهش بیشتر تحمل نسبی کاهش می یابد).


	اگر محلول کوچکتر از تلورانس مطلق باشد، اصلا دقتی وجود ندارد.


	برای DAE ها (معادلات دیفرانسیل-جبری)، می توانید معادلات جبری را از تخمین خطا حذف کنید تا خطا فقط بر اساس معادلات دیفرانسیل باشد. برای اطلاعات در مورد حذف معادلات جبری از تخمین خطا، به Advanced مراجعه کنید .

BDF در مقابل روش‌های عام آلفا و صریح

حل کننده BDF از فرمول های تمایز به عقب با ترتیب دقت متفاوت از یک (یعنی اویلر عقب مانده) تا پنج استفاده می کند. روش های BDF برای مدت طولانی مورد استفاده قرار گرفته اند و به دلیل پایداری شناخته شده اند. با این حال، آنها می توانند اثرات میرایی شدید، به ویژه روش های درجه پایین تر داشته باشند. اویلر عقب مانده به شدت فرکانس های بالا را میرا می کند. حتی اگر انتظار راه حلی با گرادیان های تیز را دارید، ممکن است به دلیل میرایی در روش اویلر معکوس، راه حلی بسیار صاف به دست آورید.

حل‌کننده α تعمیم‌یافته (آلفا) خواصی مشابه با حل‌کننده BDF مرتبه دوم دارد، اما فناوری زیربنایی متفاوت است. این شامل پارامتری است که در ادبیات α نامیده می شود تا درجه میرایی فرکانس های بالا را کنترل کند. در مقایسه با BDF (با حداکثر مرتبه دو)، α تعمیم‌یافته باعث میرایی بسیار کمتری می‌شود و در نتیجه دقیق‌تر است. به همین دلیل پایداری کمتری نیز دارد.

اجرای روش α تعمیم یافته در COMSOL Multiphysics تشخیص می دهد که کدام متغیرها از نظر زمانی مرتبه اول و کدام متغیرها از نظر زمانی مرتبه دوم هستند و فرمول های صحیح را برای متغیرها اعمال می کند.

در بسیاری از موارد، α تعمیم‌یافته یک روش دقیق با ویژگی‌های پایداری کافی است، اما روش BDF در مدیریت تغییرات در مرحله زمانی قوی‌تر و بهتر است. روش α تعمیم‌یافته برای شبیه‌سازی ترجیح داده می‌شود که گام زمانی تقریباً ثابت باشد و زمانی که میرایی کوچک یا حداقلی مورد نیاز است، مانند مشکلات ارتعاش خالص. به همین دلیل، برخی از رابط های فیزیک در COMSOL Multiphysics – برای مثال برای مکانیک ساختاری و امواج الکترومغناطیسی – از α تعمیم یافته به عنوان حل کننده گذرا پیش فرض استفاده می کنند. با این حال، برخی از مشکلات پیچیده نیاز به استحکام اضافی ارائه شده توسط روش BDF دارند.

همچنین برخی از انواع مشکل مانند سیستم‌های ODE وجود دارد که می‌توانند از دقت بالاتری که روش‌های BDF درجه بالاتر ارائه می‌کنند بهره ببرند. برای چنین سیستم‌های ODE، روش‌های صریح از خانواده روش‌های Runge-Kutta برای ODEs – RK34، Cash-Karp 5، و Dormand-Prince 5 – یا روش Adams-Bashforth می‌توانند کارآمدترین باشند. برای روش گالرکین ناپیوسته گرهی، استفاده از روش گام به گام صریح طبیعی و کارآمدتر است. موقعیت‌های دیگری که می‌تواند سودمند باشد، زمانی است که فقط از ردیابی ذرات یا مشکلات موج همراه با توده‌ای جرم استفاده می‌کنیم.

درباره رابط PDE فرم موج

بخش About Auxiliary Equation-Based Nodes برای گام‌های زمانی صریح طراحی شده است. روش بدون ربع و همچنین بدون ماتریس است. فقط ماتریس های محلی عنصر تشکیل می شوند. با تعیین متغیر wahw.wtc می توان یک گام زمانی پایدار مناسب را به طور خودکار تعیین کرد، که باید تخمینی از حداکثر سرعت موج برای معادلات در رابط باشد. سپس الگوریتم زمان صریح این سرعت را به مقیاس زمانی سلول محلی ترجمه می کند. برای یک روش راهپیمایی زمانی جهانی مانند Runge-Kutta یا Adams-Bashforth 3، گام زمانی مستقیماً با کوچکترین مقیاس زمانی سلول مرتبط است. هنگامی که تفاوت زیادی در مقیاس های زمانی سلول وجود دارد، یک روش راهپیمایی زمانی جهانی چندان کارآمد نیست. به همین دلیل، یک روش راهپیمایی زمانی محلی نیز وجود دارد، Adams–Bashforth 3 (محلی)، که سلول‌ها را بر اساس مقیاس زمانی سلولی به گروه‌هایی تقسیم می‌کند. سپس گروه‌ها با اندازه‌های گام-زمانی مختلف، به روشی کارآمدتر تبدیل می‌شوند.

روش‌های Runge–Kutta و Adams–Bashforth می‌توانند کوپلینگ‌های واسط PDE شکل موج (یا هر رابطی که از عناصر لاگرانژ ناپیوسته گره‌ای استفاده می‌کند) را با هر رابط دیگر کنترل کند. دو محدودیت وجود دارد:

•

مسئله PDE وابسته به زمان باید مرتبه اول در زمان با یک وابستگی خطی نسبت به زمان باشد

( درباره حل وابسته به زمان برای نماد مراجعه کنید).

•

اگر گسسته سازی المان محدود منجر به DAE شود، شاخص آن باید 1 باشد (به واژه نامه مراجعه کنید ). معادلات جبری با استفاده از حلگر حل می شوند . فرکانس حل این معادلات جبری را می توان با کنترل کرد که کاهش زمان محاسباتی را ممکن می سازد. به عنوان مثال، این تنظیم برای کاهش هزینه حل مشکل موج (گسسته شده با استفاده از روش گالرکین ناپیوسته گرهی) همراه با PDE بیضوی مفید است (به واژه نامه مراجعه کنید ) .

درباره حل کننده وابسته به زمان

شما چه احساسی دارید

اشتراک گذاری این مقاله :