در کتابچه راهنمای مرجع برنامه نویسی مولتیفیزیک COMSOL پیشرفته |
کدام مسائل متقارن هستند؟
هنگام استفاده از یک گره ویژگی پیشرفته ، گزینه ای برای انتخاب تقارن ماتریس دارید. اما چگونه می توان فهمید که کدام مشکلات متقارن هستند؟ هنگامی که گسسته سازی یک مسئله PDE منجر به یک ماتریس متقارن ژاکوبین (سفتی) (و یک ماتریس جرم متقارن برای مسائل وابسته به زمان یا مقادیر ویژه می شود)، اغلب می توانید الگوریتم های سریعتر و کم مصرف تری را برای حل سیستم های خطی حاصل اعمال کنید. PDE ها با گسسته سازی متقارن معمولاً در مدل هایی شامل آکوستیک، انتشار، الکترومغناطیسی، انتقال حرارت از طریق هدایت و مکانیک ساختاری رخ می دهند. در مقابل، مشکلات در مکانیک سیالات، همرفت- انتشار، و همرفت-رسانایی معمولاً شامل ماتریس های ژاکوبین نامتقارن هستند.
اگر مدل شامل اعداد مختلط باشد، می توانید بین ماتریس های متقارن و هرمیتی تمایز قائل شوید. یک ماتریس هرمیتی A را برآورده می کند
که در آن T نشان دهنده جابجایی و نوار نشان دهنده مزدوج پیچیده است.
COMSOL Multiphysics تقارن را برای ماتریس های متقارن و هرمیتی تشخیص می دهد. برای استفاده از صرفهجویی محاسباتی برای مدلهای با ماتریسهای متقارن، استفاده از حلکنندهای است که از تقارن استفاده میکند. حل کننده های سیستم خطی و پیش شرطی کننده های زیر از ماتریس های متقارن استفاده نمی کنند:
• | پیش شرط Vanka |
• | پیش شرط LU ناقص |
• | حل کننده/پیش شرطی کننده چندشبکه جبری |
انتخاب متقارن برای مسئلهای که منجر به ماتریسهای متقارن نمیشود منجر به حل نادرست میشود. |
مدیریت محدودیت حذف
مدیریت محدودیت، برای سادگی، برای یک مشکل ثابت نشان داده شده است. مدیریت برای مسائل پارامتریک، ارزش ویژه و وابسته به زمان مشابه است. سیستم جبری خطی (مقیاس شده) را در نظر بگیرید
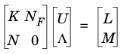
بردار ضریب لاگرانژ Λ معمولاً نامشخص است و COMSOL Multiphysics آن را حل نمی کند. به طور مشابه، محدودیت NU = M اغلب چندین بار شامل یک معادله است. برای رسیدگی به این مشکل، نرم افزار COMSOL به یک روش مدیریت محدودیت روی می آورد که از حذف استفاده می کند. حل کننده یک راه حل U d را برای محدودیت NU = M و همچنین یک ماتریس Null را محاسبه می کند که ستون های آن مبنایی برای فضای تهی N هستند . برای محدودیت های یک جهته ( N F ≠ N T ) یک ماتریس Nullfهمچنین محاسبه می شود که ستون های آن مبنایی برای فضای تهی N F T را تشکیل می دهند . سپس راه حل را به صورت U = Null U n + U d به دست می آورد . در اینجا U n حل K c U n = L c است ، که در آن
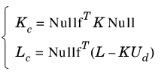
در اینجا Kc ماتریس سختی حذف شده است .
برای مسائل ارزش ویژه و وابسته به زمان، ماتریس های D و E حذف شده مربوطه هستند




