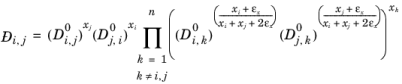این بخش شامل تعاریف مدل های موجود برای هدایت حرارتی، ویسکوزیته و انتشار است:
• | رسانایی گرمایی |
• | ویسکوزیته |
• | انتشار |
رسانایی گرمایی
بخار
ایده آل
همبستگی هدایت حرارتی بر اساس موارد زیر است:
(10-133)
تصحیح فشار Δλ v,P از روش Stiel و Thodos محاسبه می شود، رجوع کنید به Ref. 30 ، که برای ρr < 3 قابل استفاده است، اما برای H2 ، گازهای قطبی قوی، و گازهایی با درجه بالایی از پیوند هیدروژنی، مانند H 2 O و NH 3 دقت کمتری دارد.
(10-134)
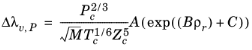
(10-135)
(10-136)
قوانین اختلاط همانطور که توسط Yorizane پیشنهاد شده است، رجوع کنید به Ref. 31 :
(10-137)
(10-138)
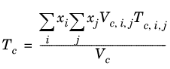
(10-139)
(10-140)
(10-141)
(10-142)
جایی که ثابت های باینری هستند
(10-143)
(10-144)
ضرایب استیل و تودوس هستند
آ | ب | سی | |
ρ r < 0.5 | A 1 = 2.702E8 | B 1 = 0.535 | C 1 = -1 |
0.5 ≤ ρ r < 2.0 | A 2 = 2.528E8 | B 2 = 0.670 | C 2 = -1.069 |
ρ r ≥ 2.0 | A 3 = 0.574E8 | B 3 = 1.155 | C 3 = 2.016 |
با این حال، برای اطمینان از تداوم مرتبه صفر در ρr = 0.5 و ρ r = 2.0، ضرایب زیر برای 0.5 ≤ ρ r < 2.0 مجدداً از
(10-145)
(10-146)
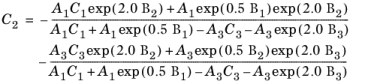
همبستگی هدایت حرارتی بخار باید برای همه گونه ها در دسترس باشد. همچنین حجم های بحرانی، Vc , i ، دماهای بحرانی، Tc ,i ، وزن های مولکولی Mi و عوامل غیرمرکز ωi باید برای همه گونه ها مشخص شوند.
نظریه جنبشی
لیندسی و بروملی (رجوع کنید به شماره 32 ) معادله ای را برای پارامترهای برهمکنش روش Wassiljewa (نگاه کنید به شماره 33 ) بر اساس نظریه جنبشی ارائه کردند تا رسانایی حرارتی مخلوط را از مقادیر گونه های خالص ارائه کنند.
(10-147)
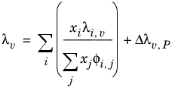
(10-148)
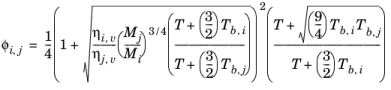
که در آن تصحیح فشار Δλ v,P از معادله 10-134 محاسبه می شود . همبستگی هدایت حرارتی بخار λi ,v و همبستگی ویسکوزیته بخار ηi ,v باید برای همه گونه ها در دسترس باشد. علاوه بر این، تمام نقاط جوش معمولی Ti ,b , وزنهای مولکولی Mi , حجمهای بحرانی Vc ,i , دماهای بحرانی Tc ,i و عوامل غیرمرکز ωi باید مشخص شوند.
آب (IAPWS)
انجمن بین المللی خواص آب و بخار معادله Ref. 34 که در محدوده زیر معتبر است:
(10-149)
(10-150)
(10-151)
مایع
مدل های مخلوط زیر برای هدایت حرارتی مایع موجود است
ایده آل
برای محاسبه رسانایی حرارتی مایع مخلوط، λl ,m ، مقادیر همبستگی های هدایت حرارتی مایع خالص به طور ایده آل مخلوط می شوند.
(10-152)
وابستگی فشار بر اساس کار Missenard ( مراجعه 51 ) است که در آن
(10-153)
که در آن Q به عنوان همبسته است
(10-154)
و از قوانین اختلاط زیر استفاده می شود
(10-155)
(10-156)
(10-157)
(10-158)
(10-159)
(10-160)
تمام همبستگی های هدایت حرارتی مایع باید مشخص شود. تمام مقادیر برای دماهای بحرانی، Tc ,i ، حجم های بحرانی، Pc ,i و فاکتورهای تراکم پذیری بحرانی، Zc ,i باید برای همه گونه های i مشخص شوند .
قانون قدرت
مقادیر همبستگی هدایت حرارتی بخار مایع خالص طبق قانون توان زیر مخلوط می شوند
(10-161)
تمام همبستگی های هدایت حرارتی مایع باید مشخص شود. این مدل برای مقادیر رسانایی حرارتی ترکیبی خالص که بیش از ضریب 2 از هم فاصله ندارند معتبر است ( مرجع 52 و مرجع 53 ). وابستگی فشار با استفاده از معادله 10-153 تا معادله 10-160 معرفی شده است . تمام مقادیر برای دماهای بحرانی، Tc ,i ، حجم های بحرانی، Pc ,i و فاکتورهای تراکم پذیری بحرانی، Zc ,i باید برای همه ادویه های i مشخص شوند .
ترکیب محلی
مدل ترکیب محلی توسط Rowley ( مراجعه 53 ) از سهم ایده آل و اضافی استفاده می کند
(10-162)
بخش ایده آل بر اساس کسرهای جرمی است
(10-163)
(10-164)
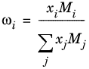
اصطلاح اضافی بر اساس غلظت های محلی NRTL است
(10-165)
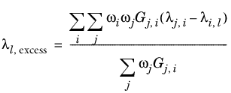
که در آن G j,i از معادله 10-58 تبعیت می کند . اصطلاحات تعامل باینری از آن پیروی می کنند
(10-166)
که متقارن است و روی مورب،
(10-167)
و
(10-168)
با ϖ i ترکیب در مخلوط دوتایی گونههای i و j است و ترکیب محلی هم مولر است.
(10-169)
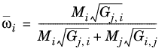
تمام همبستگی های هدایت حرارتی مایع باید مشخص شود. وابستگی فشار با استفاده از معادله 10-153 – معادله 10-160 معرفی شده است . تمام مقادیر دماهای بحرانی Tc ,i , حجم های بحرانی Pc ,i , ضرایب تراکم پذیری بحرانی Zc ,i و وزن های مولکولی M i باید برای همه ترکیبات i مشخص شوند . علاوه بر این، تمام پارامترهای تعامل باینری NRTL A i,j باید مشخص شوند. مقادیر نامشخص برای پارامترهای تعامل NRTL B i,j روی صفر تنظیم شده است. پارامترهای تصادفی α i,jدارای مقادیر صفر در مورب و ماتریس متقارن است. تمام مقادیر خارج از مورب باید مشخص شوند. مدل NRTL در معادله 10-54 تا معادله 10-65 ارائه شده است .
ترکیب محلی (اصلاح شده)
رولی ( مراجعه 52 ) مدل ترکیب محلی را با جایگزین کردن قاعده اختلاط در معادله 10-166 با موارد زیر تطبیق داد.
(10-170)
که او دریافت که در بیشتر مواردی که هم مدل ترکیب محلی و هم مدل قانون قدرت مشکل دارند، پیشبینیهای مدل بهتری تولید میکند. با این حال، مدل به طور کلی قابل اجرا نیست. به عنوان مثال، سیستم های حاوی H 2 O به دلیل وزن مولکولی پایین H 2 O به خوبی توسط این مدل توصیف نشده اند.
آب (IAPWS)
انجمن بین المللی خواص آب و بخار معادله Ref. 34 که در محدوده زیر معتبر است:
(10-171)
(10-172)
(10-173)
ویسکوزیته
بخار
ویلکه
ویلکه، رجوع کنید به رفر. 35 ، روش خود را برای ویسکوزیته مخلوط فاز بخار بر اساس نظریه جنبشی استوار کرد:
(10-174)
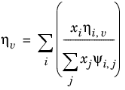
(10-175)
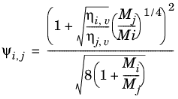
همبستگی ویسکوزیته بخار ηi ,v باید برای همه گونه ها موجود باشد. علاوه بر این، تمام وزن های مولکولی M i باید مشخص شوند.
بروکاو
Brokaw (نگاه کنید به مرجع 36 ) از همان معادله اولیه Wilke استفاده می کند ( معادله 10-174 ). با این حال، معادله 10-175 با
(10-176)
و پارامتر تعامل به صورت تعریف شده است
(10-177)
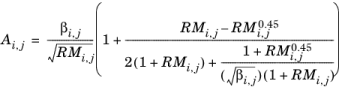
جایی که
(10-178)  ،
،
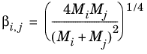 ،
،همبستگی ویسکوزیته بخار، ηi ,v باید برای همه گونههای i موجود باشد . علاوه بر این، تمام وزن های مولکولی M i باید مشخص شوند. اگر انرژی لنارد-جونز ε i (مراجعه کنید به شماره 37 ) پارامتر قطبی استوکمایر δs ,i ( مراجعه 38 و رفر. 39 ) برای هر دو گونه i و j مشخص شده است، پس
(10-179)
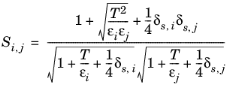
در غیر این صورت،
(10-180)
دیویدسون
روش دیویدسون، رجوع کنید به رفر. 40 ، به پارامترهای خاص ترکیب کمتری نسبت به Brokaw نیاز دارد، در حالی که دقت گزارش شده تقریباً به همان اندازه خوب است، و در مورد H 2 ، حتی از آن نیز فراتر می رود. مدل دیویدسون فقط به جرم مولی و ویسکوزیته گازهای خالص نیاز دارد. این مدل بر اساس سیالیت است که به عنوان ویسکوزیته متقابل تعریف می شود.
(10-181)
سپس سیالیت مخلوط به صورت زیر محاسبه می شود:
(10-182)
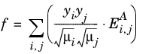
که در آن y i کسر تکانه گونه i است ، E i,j ضریب انتقال تکانه جفت گونه i، j ، و A یک پارامتر مستقل گونه تجربی است که روی 1/3 تنظیم شده است. کسر حرکت به صورت زیر بدست می آید:
(10-183)
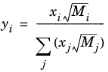
و ضریب انتقال حرکت به صورت زیر در نظر گرفته می شود:
(10-184)
اصلاح فشار بالا
برای در نظر گرفتن تأثیر فشار بر ویسکوزیته بخار، می توان از اصلاح فشار استفاده کرد. وابستگی فشار بر اساس تئوری گاز جنبشی است که عبارت زیر را به ویسکوزیته بخار اضافه می کند:
(10-185)
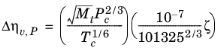
که در آن ξ از همبستگی Jossi ( مراجعه 41 ) محاسبه می شود که برای ρr < 3.0 قابل استفاده است. برای H2 ، گازهای قوی قطبی و گازهایی با درجه بالایی از پیوند هیدروژنی مانند H2O و NH3 دقت کمتری دارد .
ضریب تصحیح به دلیل استفاده از واحدهای فشار، اتمسفر و ویسکوزیته، cP، در همبستگی جوسی است. به صورت زیر بیان می شود:
(10-186)

(10-187)
(10-188)
قوانین مخلوط زیر استفاده می شود
(10-189 )  ،
،

(10-190)  ،
،
مقادیر برای حجم های بحرانی، Vc ,i ، دماهای بحرانی، Tc ,i ، عوامل تراکم پذیری بحرانی، Zc ،i و وزن های مولکولی، M i باید برای همه گونه های i مشخص شود .
اصلاح فشار بالا برای مدل های مخلوط Wilke، Brokaw و Davidson موجود است. ویسکوزیته بخار ناشی از
(10-191)
که در آن η v، Wilke از معادله 10-174 محاسبه می شود .
مدل ایالات متناظر پدرسن
مدل ویسکوزیته حالت های متناظر پدرسن ( مرجع 42 و رفرنس 43 ) برای هر دو فاز بخار و مایع مخلوط های هیدروکربنی اعمال می شود. گونه مرجع انتخاب شده CH 4 است .
ویسکوزیته CH 4 از Ref محاسبه می شود. 44 ، اصلاح شده توسط Pedersen و Fredenslund ( مراجعه 45 ) برای جلوگیری از مسائل زیر 91 K که در آن CH 4 جامد می شود
(10-192)
جایی که
(10-193)
(10-194)
(10-195)
(10-196)
در اینجا ρ CH 4 در g/cm 3 استفاده می شود . برای تبدیل جرم به مول ρ CH 4 ، از وزن مولکولی M CH 4 = 16.042568 گرم بر مول استفاده می شود.
قسمت گاز رقیق شده توسط
(10-197)
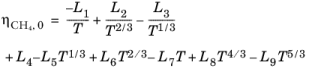
اولین تصحیح چگالی برای گاز با چگالی متوسط توسط
(10-198)
بقیه با همبستگی تجربی به دست می آید
(10-199)
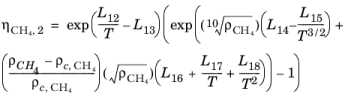
عبارت تصحیح برای CH 4 جامد
(10-200)
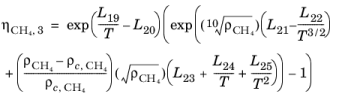
با مقادیر پارامترهای L 1 تا L 25 در جدول 10-5 در زیر آمده است :
L 1 | 2.090975·10 5 | L 10 | 1.696985927 | L 19 | 9.74602 |
L2 _ | 2.647269·10 5 | L 11 | 0.133372346 | L 20 | 44.6055 |
L 3 | 1.472818·10 5 | L 12 | 188.73011594 | L 21 | 18.0834 |
L 4 | 47167.40 | L 13 | 10.35060586 | L22 _ | 4126.66 |
L 5 | 9491.827 | L 14 | 17.571599671 | L23 _ | 0.976544 |
L 6 | 1219.979 | L 15 | 3019.3918656 | L24 _ | 81.8134 |
L7 _ | 96.27993 | L 16 | 0.042903609488 | L25 _ | 15649.9 |
L 8 | 4.274152 | L 17 | 145.29023444 | ||
L9 _ | 0.08141531 | L 18 | 6127.6818706 |
در اینجا ρ CH 4 در g/cm 3 استفاده می شود . چگالی بحرانی با ρc , CH 4 = 0.16284 g/cm 3 داده می شود . معادله زیر توسط مک کارتی ( مرجع 46 ) برای چگالی CH 4 حل شده است.
(10-201)
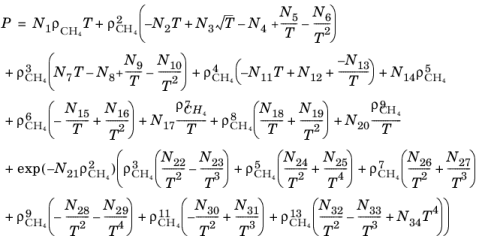
که در آن ρ CH 4 در mol/l استفاده می شود.
شماره 1 | 0.08205616 | شماره 13 | 2.8685285973 | N25 _ | 1.6428375992·10 6 |
N2 _ | 0.018439486666 | شماره 14 | 0.11906973942·10 -3 | N 26 | 0.21325387196 |
N3 _ | 1.0510162064 | شماره 15 | 0.0085315715699 | N27 _ | 37.791273422 |
N 4 | 16.057820303 | N 16 | 3.8365063841 | N 28 | 0.1185701681·10 -4 |
N5 _ | 848.44027562 | N17 _ | 0.24986828379·10 -4 | N29 _ | 31.630780767 |
N6 _ | 42738.409106 | شماره 18 | 0.57974531455·10 -5 | N30 _ | 0.4100678294·10 -5 |
N7 _ | 0.76565285254·10 -3 | N19 _ | 0.0071648329297 | N31 _ | 0.0014870043284 |
N8 _ | 0.48360724197 | شماره 20 | 0.12577853784·10 -3 | N32 _ | 3.151226153·10 -9 |
N9 _ | 85.195473835 | N 21 | 0.0096 | N33 _ | 0.2167077474·10 -5 |
N 10 | 16607.434721 | N22 _ | 22240.102466 | N34 _ | 0.2400055107·10 -4 |
N 11 | 0.37521074532·10 -4 | N23 _ | 1.4800512328·10 6 | ||
N 12 | 0.028616309259 | N24 _ | 50.498054887 |
با ویسکوزیته و چگالی CH 4 تعریف شده، ویسکوزیته هر مخلوط، ηm را می توان از اصل حالت های مربوطه محاسبه کرد.
(10-202)
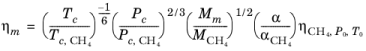
که در آن ویسکوزیته CH 4 ρ CH4 , P 0 , T 0 در دمای T 0 و فشار P 0 محاسبه می شود :
(10-203)
(10-204)
قوانین اختلاط زیر برای خواص بحرانی استفاده می شود، رجوع کنید به Ref. 47 :
(10-205)
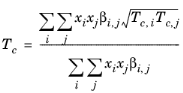
(10-206)
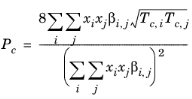
(10-207)
پارامتر α است
(10-208)
(10-209)
جایی که
(10-210)
(10-211)
با ρc ,CH 4 = 0.16284 g/ cm 3 . برای CH 4
(10-212)
که در آن از معادله 10-209 استفاده شده است. وزن مولکولی مخلوط تابعی از وزن مولکولی میانگین وزنی و وزن مولکولی میانگین عددی است.
(10-213)
(10-214)
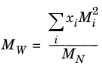
(10-215)
که در آن توان در معادله 10-213 با برازش داده های ویسکوزیته تجربی تعیین می شود.
توجه داشته باشید که همبستگی ویسکوزیته بخار گونه خالص ηi ,v مورد نیاز نیست. با این حال، برای هر گونه i ، وزن مولکولی Mi ، دمای بحرانی، Tc ,i ، و فشار بحرانی، Pc , i باید مشخص شود.
آب (IAPWS)
انجمن بین المللی خواص آب و بخار معادله Ref. 48 – ر. 49 برای کاربرد صنعتی که در محدوده زیر معتبر است:
(10-216)
(10-217)
(10-218)
(10-219)
(10-220)
که در آن T m دمای ذوب وابسته به فشار و p t فشار سه نقطه است. مطابق با توصیه های کاربردی صنعتی، اصلاح ناحیه بحرانی اعمال نمی شود.
مایع
مدل های مخلوط زیر برای ویسکوزیته مایع موجود است.
اختلاط لگاریتمی مولار
مقادیر ویسکوزیته مایع لگاریتم گونه های خالص، ln ηi ,l به طور ایده آل با استفاده از کسرهای مول x i مخلوط می شوند.
(10-221)
که در آن η m,l ویسکوزیته مخلوط مایعات است.
اختلاط لگاریتمی جرمی
مقادیر همبستگی ویسکوزیته مایع لاگ گونه های خالص به طور ایده آل با استفاده از کسر وزن ω i مخلوط می شوند.
(10-222)
مدل ایالات متناظر پدرسن
مدل ایالات متناظر پدرسن که در بالا برای ویسکوزیته فاز گاز توضیح داده شد، برای فاز مایع نیز اعمال می شود. همبستگی ویسکوزیته مایع گونه خالص مورد نیاز نیست. با این حال، برای هر گونه i ، وزن مولکولی Mi ، دمای بحرانی Tc ,i و فشار بحرانی Pc , i باید مشخص شود.
اختلاط مکعبی
ویسکوزیته مخلوط با استفاده از میانگین ریشه مکعبی بر حسب کسر مول x i تعریف می شود.
(10-223)
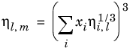
مدل در Ref. 50 برای ارائه نتایج معقول برای مخلوط هیدروکربنی از اجزای مشابه.
مدل مستلزم آن است که همبستگی ویسکوزیته مایع ورود به سیستم برای همه گونههای i موجود باشد .
مخلوط کردن توده مکعبی
معادل کسر جرمی مدل قبلی است
(10-224)
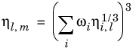
مدل مستلزم آن است که همبستگی ویسکوزیته مایع ورود به سیستم برای همه گونههای i موجود باشد .
آب (IAPWS)
انجمن بین المللی خواص آب و بخار معادله Ref. 48 – ر. 49 برای کاربرد صنعتی که در محدوده زیر معتبر است:
(10-225)
(10-226)
(10-227)
(10-228)
(10-229)
که در آن  دمای ذوب وابسته به فشار و
دمای ذوب وابسته به فشار و  فشار سه نقطه است. مطابق با توصیه های کاربردی صنعتی، اصلاح ناحیه بحرانی اعمال نمی شود.
فشار سه نقطه است. مطابق با توصیه های کاربردی صنعتی، اصلاح ناحیه بحرانی اعمال نمی شود.
انتشار
دو نوع ضریب انتشار پشتیبانی می شود. ضرایب انتشار در سیستم های بی نهایت رقیق، و ضرایب انتشار ماکسول-استفان.
برای سیستم های رقیق، ضریب انتشار باینری D 0 i , j نشان دهنده نفوذ گونه i در محیطی متشکل از گونه های خالص j است . این مربوط به ضریب انتشار فیکی است.
ضریب انتشار فاز گاز در رقت بی نهایت
مدل های زیر برای ضرایب انتشار در رقت بی نهایت در فاز بخار موجود است:
• | فولر-شتلر-گیدینگ |
• | ویلکه-لی |
خودکار
هنگامی که مدل ویژگی انتشار گاز روی خودکار تنظیم می شود، از مدل فولر-شتلر-گیدینگز استفاده می شود، مشروط بر اینکه حجم انتشار فولر برای هر دو گونه ( i و j) شناخته شده باشد ، در غیر این صورت مدل Wilke-Lee استفاده می شود.
فولر-شتلر-گیدینگ
فولر و دیگران ( مراجعه 58 ) رابطه Chapman-Enskog را برای همبستگی ضریب انتشار باینری برای گونه های i و j در فاز بخار مطابق با مدل فولر-شتلر-گیدینگ (FGS) اصلاح کردند:
(10-230)
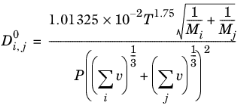
که در آن T دما (K)، M i وزن مولکولی گونه i (g/mol ) و P فشار (Pa) است. v i حجم های انتشار اتمی هستند (حجم انتشار کامل، سانتی متر 3 )، که با استفاده از مشارکت گروهی برای هر گونه تخمین زده می شود ( مراجعه 59 ):
گروه | مشارکت |
سی | 15.9 |
اچ | 2.31 |
O | 6.11 |
ن | 4.54 |
اف | 14.7 |
Cl | 21 |
برادر | 21.9 |
من | 29.8 |
اس | 22.9 |
انگشتر معطر | -18.3 |
حلقه هتروسیکلیک | -18.3 |
برای برخی از مولکول های ساده از مقادیر زیر که از رگرسیون تعیین می شود استفاده می شود:
گونه ها | حجم انتشار فولر |
او | 2.67 |
آره | 5.98 |
آر | 16.2 |
Kr | 24.5 |
ماشین | 32.7 |
H2 _ | 6.12 |
D2 _ | 6.84 |
N2 _ | 18.5 |
از 2 | 16.3 |
CO | 18 |
CO2 _ | 26.9 |
N 2 O | 35.9 |
NH3 _ | 20.7 |
H 2 O | 13.1 |
SF 6 | 71.3 |
Cl 2 | 38.4 |
Br2 _ | 69 |
SO2 _ | 41.8 |
هوا | 19.7 |
ویلکه-لی
Wilke و Lee ( مراجعه 60 ) همچنین رابطه Chapman-Enskog را برای همبستگی ضریب انتشار باینری در فاز بخار با توجه به:
(10-231)
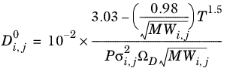
جایی که
(10-232)
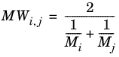
مقیاس طول  برای تعامل از پارامترهای قطر لنارد-جونز گونههای i و j گرفته شده است :
برای تعامل از پارامترهای قطر لنارد-جونز گونههای i و j گرفته شده است :
(10-233)
اگر  در پایگاه داده مشخص نشده باشد، در عوض از زیر تخمین زده می شود:
در پایگاه داده مشخص نشده باشد، در عوض از زیر تخمین زده می شود:
(10-234)
که در آن V i,l,b حجم مولی گونه ها در نقطه جوش نرمال است.
انتگرال برخورد Ω D از ( مراجعه 61 ) ارزیابی می شود :
(10-235)
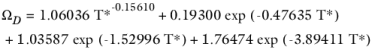
با
(10-236)
مقیاس انرژی εi , j برای برهمکنش از پارامترهای انرژی لنارد-جونز گونههای i و j گرفته شده است :
(10-237)
اگر  در پایگاه داده مشخص نشده باشد، در عوض از زیر تخمین زده می شود:
در پایگاه داده مشخص نشده باشد، در عوض از زیر تخمین زده می شود:
(10-238)
که در آن k ثابت بولتزمن و T i , l , b دمای نقطه جوش نرمال است.
فاز گاز ماکسول-استفان انتشار
برای انتشار فاز گاز، انتشار ماکسول-استفان از مدلهای انتشار فاز گاز در رقت بینهایت تعریف شده است.
(10-239)
همه مدلهای انتشار فاز گاز در رقت بینهایت متقارن هستند، میزان انتشار گونه i در گونه j برابر است با گونه j در گونه i . علاوه بر این، تحت فرض گاز ایده آل، ضریب انتشار ماکسول-استفان با ضریب انتشار فیک مطابقت دارد. این نشان می دهد که انتشار گاز ماکسول-استفان ارائه شده مستقل از ترکیب است.
ضرایب انتشار فاز مایع در رقت بی نهایت
مدل های زیر برای ضرایب انتشار در رقت بی نهایت در فاز مایع موجود است:
• | ویلکه-چانگ |
• | تین – کالوس |
• | هایدوک–مینهاس |
• | صدیقی – لوکاس |
• | ارکی-رودن-آکگرمن |
خودکار
هنگامی که مدل انتشار مایع در مدل ویژگی رقت نامتناهی روی خودکار تنظیم می شود، انتخابی برای هر املاح i در حلال j از مدل ها مطابق قوانین زیر انجام می شود. به جز در مورد همبستگی دما و مدل ارکی-رودن-آکگرمن ، همه این قوانین مستلزم این هستند که همبستگی لگ ویسکوزیته مایع، ln ηj در پایگاه داده برای گونه j موجود باشد و حجم مایع در نقطه جوش معمولی، V i ,l,b برای گونه i موجود است .
• | اگر همبستگی دما برای گونه های i و j موجود باشد ، از آن استفاده می شود. |
• | اگر حلال آب باشد، از همبستگی صدیقی-لوکاس (برای سیستم های آبی) استفاده می شود. |
• | اگر محلول و حلال هر دو پارافین معمولی باشند، از همبستگی هایدوک-مینهاس (برای پارافین های معمولی) استفاده می شود. |
• | اگر حلال یک پارافین معمولی باشد، و همبستگی چگالی مایع برای حلال در دسترس باشد، و املاح هیدروژن، کربن مونوکسید یا دی اکسید کربن باشد، از همبستگی ارکی-رودن-آکگرمن (برای پارافین های معمولی) استفاده می شود. |
• | اگر پاراکورهای P i و Pj هر دو در دسترس باشند و حجم مایع در نقطه جوش معمولی، V i ,l,b برای حلال موجود باشد، از همبستگی Tyn-Calus استفاده میشود. |
• | اگر پاراچورهای P i و P j هر دو در دسترس باشند، از همبستگی هایدوک-مینهاس استفاده می شود. |
• | اگر املاح و حلال هر دو مولکول آلی و حجم مایع در نقطه جوش معمولی باشند، V i ,l,b برای حلال موجود باشد، از روش صدیقی-لوکاس استفاده می شود. |
• | اگر وزن مولکولی Mj برای حلال موجود باشد، از همبستگی Wilke-Chang استفاده می شود. |
• | اگر حلال یک پارافین معمولی باشد، و همبستگی چگالی مایع برای حلال در دسترس باشد، و املاح یک پارافین معمولی باشد، از همبستگی Erkey–Rodden–Akgerman (برای پارافینهای معمولی) استفاده میشود. |
• | اگر حلال یک پارافین معمولی باشد، و همبستگی چگالی مایع برای حلال موجود باشد، و قطر لنارد-جونز برای املاح موجود باشد، از همبستگی ارکی-رودن -آکگرمن (برای پارافین های معمولی) استفاده می شود. |
برای روش صدیقی-لوکاس ، یک مولکول در صورتی آلی در نظر گرفته می شود که حداقل یک اتم C به هر چیزی غیر از اتم های O یا C متصل باشد. این با فرمول SMILES در صورت وجود تعیین می شود. اگر برای هر جفت گونه، داده های ورودی مورد نیاز برای هیچ یک از مدل های بالا در دسترس نباشد، ضریب انتشار مایع در رقت نامحدود در دسترس نیست.
ویلکه-چانگ
همبستگی Wilke و Chang ( مراجعه 62 ) برای ضرایب انتشار فاز مایع در رقت بی نهایت است:
(10-240)
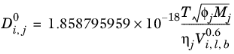
وزن مولکولی، Mj و log همبستگی ویسکوزیته مایع، برای گونه j و حجم مولی مایع در نقطه جوش نرمال برای گونه i ،، مورد نیاز است. پارامتر ارتباط Wilke-Chang ، اگر در دسترس نباشد، به صورت زیر تنظیم می شود:


حلال | پارامتر ارتباط |
اب | 2.26 ( مراجعه 63 ) |
متانول | 1.9 |
اتانول | 1.5 |
دیگران | 1 |
گونه ها با شماره CAS یا فرمول SMILES شناسایی می شوند. همبستگی Wilke-Chang برای انتشار آب مناسب نیست. اگر آب حل شونده باشد، تصحیح پیشنهاد شده توسط Kooijman ( مراجعه 64 ) در جایی اعمال می شود که حجم مولی مایع آب در نقطه جوش معمولی، V آب، l,b در 4.5 ضرب شود.
تین – کالوس
همبستگی تین و کالوس ( مراجعه 65 ) برای ضرایب انتشار مایع در رقت نامحدود می گوید:
(10-241)
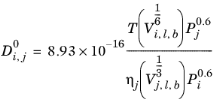
همبستگی لگاریتم گرانروی مایع ln ηj باید برای گونه های j در دسترس باشد ، حجم مایع در نقطه جوش معمولی، V i ،l،b و parachor، P i باید برای هر دو گونه i و j در دسترس باشد .
اگر حلال غیرقطبی باشد (ممان دوقطبی صفر است)، و حلال متانول، اتانول یا 1-بوتانول باشد یا اگر حلال یک الکل مونو هیدروکسی باشد، حجم مایع در نقطه جوش نرمال، Vj,l , b و parachor، P j با ضریب 8 × 10 3 η j تصحیح می شود .
اگر املاح آب باشد، هر دو حجم مایع در نقطه جوش نرمال، V i,l,b و parachor, Pi برای املاح با ضریب 2 تصحیح می شوند. این ضریب همچنین در صورتی اعمال می شود که از فرمول SMILE تشخیص داده شود که گونه یک اسید آلی است (یک گروه کربوکسیل یافت می شود)، به جز در مواردی که حلال آب، متانول یا n-بوتانول باشد.
هایدوک–مینهاس
Hayduk و Minhas ( مراجعه 66 ) سه همبستگی مختلف را برای ضرایب انتشار مایع در رقت بی نهایت پیشنهاد کردند.
محلول های آبی : در صورتی که حلال آب باشد (برگرفته از شماره CAS یا فرمول SMILES)، همبستگی به شرح زیر است:
(10-242)
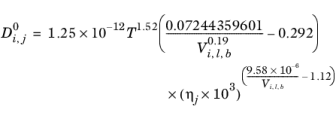
محلول های پارافین معمولی : در صورتی که هر دو محلول و حلال پارافین های معمولی باشند (مشتق شده از فرمول SMILES)، همبستگی به شرح زیر است:
(10-243)
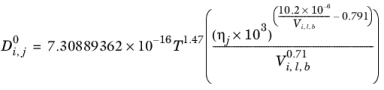
برای همه سیستم های دیگر، همبستگی این است:
(10-244)
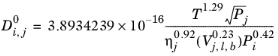
اگر حلال غیرقطبی باشد (ممان دوقطبی صفر است)، و حلال متانول، اتانول یا 1-بوتانول باشد یا اگر حلال یک الکل مونو هیدروکسی باشد، حجم مایع در نقطه جوش نرمال، Vj,l , b و parachor، P j با ضریب تصحیح می شوند  .
.
اگر املاح آب باشد ، حجم مایع در نقطه جوش نرمال، V i,l,b و parachor, Pi برای املاح با ضریب 2 تصحیح می شود. این عامل همچنین در صورتی اعمال می شود که از فرمول SMILES مشخص شود که گونه ها یک اسید آلی است (یک گروه کربوکسیل یافت می شود)، به جز در مواردی که حلال آب، متانول یا n-بوتانول باشد.
صدیقی – لوکاس
صدیقی و لوکاس ( مراجعه 67 ) همبستگی هایی را برای ضرایب انتشار مایع در رقت بی نهایت برای سیستم آبی (از جمله گازها) و برای محلول های آلی پیشنهاد کردند. برای سیستم های پارافین معمولی، آنها مدل Hayduk-Minhas را توصیه کردند .
برای محلول های آبی:
(10-245)
برای تمام سیستم های دیگر، معادله محلول آلی به صورت زیر استفاده می شود:
(10-246)
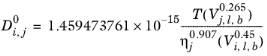
در جایی که T دما است، V i ,l,b حجم مایع در نقطه جوش معمولی و ηj ویسکوزیته حلال است.
ارکی-رودن-آکگرمن
همبستگی توسط Erkey و دیگران ( مراجعه 68 ) برای ضرایب انتشار مایع در رقت نامحدود در پارافین های معمولی است:
(10-247)
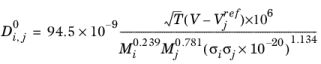
جایی که حجم مرجع است
(10-248)
N Av عدد آووگادرو است و انحراف از نزدیکترین حجم بسته بندی با داده می شود
(10-249)
این همبستگی به پارافین های معمولی، هیدروژن، مونوکسید کربن و دی اکسید کربن منتشر شده در پارافین های معمولی برازش داده می شود. وزن مولکولی M i باید هم برای املاح و هم برای حلال موجود باشد. قطر Lennard-Jones, σi از روش مشارکت گروه Bondi ( مراجعه 69 ) تخمین زده می شود، و برای برخی از گونه ها از Ref. 68 و رفر. 70 به عنوان:
گونه ها | |
H2 _ | 2.92 |
CO | 3.72 |
CO2 _ | 3.97 |
nC j H 2j + 2 | (21.82+32.44*j) 1/3 |
برای جلوگیری از منفی شدن ضرایب انتشار، حداقل اختلاف ( V – Vj ref ) 10-12 mol/m3 در نظر گرفته می شود .
فاز مایع ماکسول-استفان انتشار
ضرایب انتشار مایع ماکسول-استفان از ضرایب انتشار مایع در رقت بی نهایت محاسبه می شود. مقادیر مورب باید نادیده گرفته شوند و روی صفر تنظیم شوند. مدل Vignes ( مراجعه 71 ) برای انتشار در محلول های دوتایی را می توان به سیستم های چند جزئی گسترش داد ( مرجع 72 ):
(10-250)
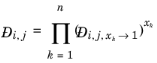
که  نشاندهنده ضریب انتشار مایع ماکسول-استفان برای گونههای i و j در محدود گونههای خالص k است . اگر k = j ، یک سیستم دوتایی از گونه های i و j را نشان می دهد که در آن i بی نهایت رقیق شده است. علاوه بر این، در رقت نامتناهی، ضریب ترمودینامیک (فعالیت) ( مراجعه 57 ) به وحدت تبدیل می شود و انتشار ماکسول-استفان برابر با انتشار فیک است:
نشاندهنده ضریب انتشار مایع ماکسول-استفان برای گونههای i و j در محدود گونههای خالص k است . اگر k = j ، یک سیستم دوتایی از گونه های i و j را نشان می دهد که در آن i بی نهایت رقیق شده است. علاوه بر این، در رقت نامتناهی، ضریب ترمودینامیک (فعالیت) ( مراجعه 57 ) به وحدت تبدیل می شود و انتشار ماکسول-استفان برابر با انتشار فیک است:
(10-251)
به همین ترتیب،
(10-252)
مدلهای برای  k ≠ i و k ≠ j باید به گونهای تعریف شوند که از تقارن اطمینان حاصل شود:
k ≠ i و k ≠ j باید به گونهای تعریف شوند که از تقارن اطمینان حاصل شود:
(10-253)
و برای اطمینان از تداوم اگر هر دو گونه i و j ناپدید شوند:
(10-254)
برای سیستم های باینری، معادله 10-250 به فرمول درون یابی ویگن کاهش می یابد.
وسلینگ – کریشنا
وسلینگ و کریشنا ( مراجعه 72 ) پیشنهاد کردند:
(10-255)
منجر به:
(10-256)
کویجمن–تیلور
Kooijman و Taylor ( مراجعه 73 ) در تعداد محدودی از سیستم ها دریافتند که نتایج بهتری ارائه می دهد:
(10-257)
منجر به:
(10-258)
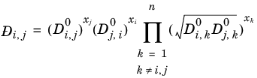
Wesselingh و Bollen ( مراجعه 74 ) اظهار داشتند که این یک برآورد معقول است.
کریشنا-وان باتن
کریشنا و ون باتن ( مراجعه 75 )، بر اساس دادههای بهدستآمده از شبیهسازیهای دینامیکی مولکولی، درونیابی مبتنی بر Vignes ( مراجعه 71 ) زیر را پیشنهاد کردند:
(10-259)
این مدل برای x i = x j به مدل Kooijman–Taylor کاهش می یابد . مقدار of در حد x i → 0 و x j → 0 تعریف نشده است . از نقطه نظر فیزیکی این بی اهمیت است زیرا مقدار در عبارات به دست آمده برای شارها با استفاده از معادلات ماکسول-استفان لغو می شود. با این وجود، برای به دست آوردن مقادیر و مشتقات ترکیبی کاملاً تعریف شده خود، معادله به شکل زیر اصلاح میشود:

(10-260)
که در آن ε x = 10-10 به عنوان یک ترکیب کوچک در نظر گرفته می شود. حالت محدود کننده برای هر دو x i → 0 و x j → 0 نیز به مدل Kooijman-Taylor کاهش می یابد . این معادله منجر به:
(10-261)