معادلات ارائه شده در اینجا معادلات جریان پتانسیل خطی شده هستند. این امر کاربردهای رابط فیزیک را به سیستم‌هایی محدود می‌کند که در آن جریان پس‌زمینه به‌خوبی توسط یک جریان پتانسیل تراکم‌پذیر توصیف می‌شود، یعنی جریانی که غیر لزج، باروتروپیک و غیر چرخشی است. منابع صوتی نیز باید خارج از جریان باشند یا حداقل باید با منابع ساده و به خوبی تعریف شده نشان داده شوند. حوزه‌های کاربردی معمولاً شامل مدل‌سازی نحوه تأثیر نویز موتور جت تحت تأثیر جریان متوسط است.
متغیر وابسته اساسی پتانسیل سرعت است که 
به طور مرسوم توسط رابطه تعریف می شود
به طور مرسوم توسط رابطه تعریف می شود
که در آن u = u ( r , t ) سرعت ذره مرتبط با حرکت موج صوتی است. سرعت کل ذرات با استفاده از
(5-9)
جایی که V نشان‌دهنده سرعت متوسط محلی برای حرکت سیال است (میانگین جریان در رابط‌های خطی شده اویلر و ناویر-استوکس با برچسب u 0 مشخص می‌شود). معادلات دینامیکی این میدان جریان متوسط در زیربخش بعدی توضیح داده شده است. در حال حاضر، فقط V را یک میدان سرعت پس زمینه چرخشی معین فرض کنید. از این رو، سرعت جریان متوسط را نیز می توان بر حسب میدان پتانسیل Φ ، با V = ∇Φ تعریف کرد .
معادله خطی شده برای پتانسیل سرعت ، حاکم بر امواج صوتی در جریان پس‌زمینه با میانگین سرعت زمینه V ، میانگین چگالی پس‌زمینه ρ 0 و میانگین سرعت پس‌زمینه صوت c 0 است.
، حاکم بر امواج صوتی در جریان پس‌زمینه با میانگین سرعت زمینه V ، میانگین چگالی پس‌زمینه ρ 0 و میانگین سرعت پس‌زمینه صوت c 0 است.(5-10)
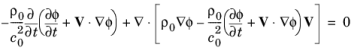
در استخراج این معادله، تمامی متغیرهای موجود در معادلات کامل غیرخطی سیالات دینامیک ابتدا به روش معادله 5-9 به بخش‌های مستقل از زمان و آکوستیک تقسیم شدند . سپس، خطی کردن معادلات حاصل در آشفتگی صوتی و حذف همه متغیرهای صوتی به جز پتانسیل سرعت، معادله 5-10 را به دست می‌دهد . بنابراین، چگالی ρ در این معادله، بخش مستقل از زمان است. قسمت آکوستیک مربوطه ρ ( r , t ) = p ( r , t )/ c02 است که در آن p فشار آکوستیک است که توسط
از این رو، هنگامی که معادله 5-10 برای پتانسیل سرعت حل شد، فشار آکوستیک به راحتی قابل محاسبه است.
هنگامی که به حوزه فرکانس تبدیل می شود، معادله موج 5-10 خوانده می شود
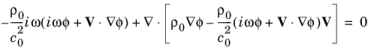
در حالی که فشار آکوستیک است
شرایط مرزی معمولی عبارتند از:
• | مرزها یا دیوارهای سخت صدا |
• | مرزهای صدا-نرم |
• | شرایط مرزی امپدانس |
• | شرایط مرزی تشعشع |
معادلات دامنه فرکانس
در حوزه فرکانس پتانسیل سرعت یک موج هارمونیک فرم فرض می شود
یک موج هارمونیک فرم فرض می شود
معادله حوزه فرکانس حاکم – یا معادله هارمونیک زمان – است
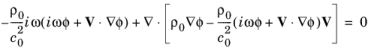
در دو بعدی، جایی که
هنگامی که عملگرهای ∇ بسط می یابند، عدد موج خارج از صفحه kz وارد معادلات می شود :
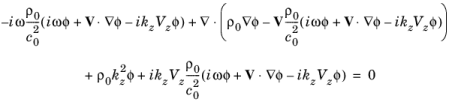
مقدار پیش فرض عدد موج خارج از صفحه 0 است ، یعنی هیچ انتشار موجی عمود بر صفحه دوبعدی وجود ندارد. در تحلیل مد معادلات برای kz حل می شوند .
برای اجزای متقارن محوری دو بعدی
عدد موج آزیموتال m به طور مشابه در معادله به عنوان یک پارامتر ظاهر می شود:
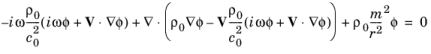
 | میدان سرعت پس‌زمینه V نمی‌تواند مولفه‌ای ازیموتال داشته باشد زیرا جریان غیر چرخشی است. |
معادله وابسته به زمان
در حوزه زمان، رابط فیزیک پتانسیل سرعت را با یک وابستگی گذرا دلخواه حل می کند. معادله زیر بر امواج صوتی در یک جریان پتانسیل متوسط حاکم است:
با یک وابستگی گذرا دلخواه حل می کند. معادله زیر بر امواج صوتی در یک جریان پتانسیل متوسط حاکم است:(5-11)
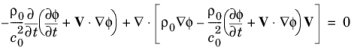
در اینجا ρ 0 (واحد SI: kg/m3 ) میانگین چگالی جریان پس‌زمینه است، V (واحد SI: m/s) نشان‌دهنده میانگین سرعت پس‌زمینه است، و c 0 (واحد SI: m/s) به سرعت صدا. نرم افزار معادله پتانسیل سرعت را با واحد SI m2 / s حل می کند. اعتبار این معادله بر این فرض استوار است که ρ 0 , V , و c 0 تقریباً در زمان ثابت هستند، در حالی که می توانند توابعی از مختصات مکانی باشند.
با واحد SI m2 / s حل می کند. اعتبار این معادله بر این فرض استوار است که ρ 0 , V , و c 0 تقریباً در زمان ثابت هستند، در حالی که می توانند توابعی از مختصات مکانی باشند. | میدان سرعت پس‌زمینه V نمی‌تواند مولفه‌ای ازیموتال داشته باشد زیرا جریان غیر چرخشی است. |
تجزیه و تحلیل حالت مرزی
نوع تحلیل حالت مرزی در سه بعدی از حل کننده مقدار ویژه برای حل معادله استفاده می کند
(5-12)
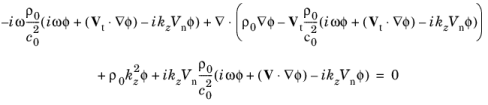
برای حالت‌های ویژه ، و مقادیر ویژه، λ = – ik z ، در یک دامنه دو بعدی محدود، Ω ، با توجه به شرایط لبه‌ای که به خوبی در ∂Ω قرار دارند . در این معادله، پتانسیل سرعت، ρ 0 میانگین چگالی جریان پس‌زمینه، c 0 سرعت صوت، ω فرکانس زاویه‌ای، و kz عدد موج خارج از صفحه یا ثابت انتشار است . علاوه بر این، V t نشان‌دهنده میانگین سرعت پس‌زمینه در صفحه مماسی است در حالی که Vn مولفه میانگین سرعت پس‌زمینه در جهت عادی است .
، و مقادیر ویژه، λ = – ik z ، در یک دامنه دو بعدی محدود، Ω ، با توجه به شرایط لبه‌ای که به خوبی در ∂Ω قرار دارند . در این معادله، 
پتانسیل سرعت، ρ 0 میانگین چگالی جریان پس‌زمینه، c 0 سرعت صوت، ω فرکانس زاویه‌ای، و kz عدد موج خارج از صفحه یا ثابت انتشار است . علاوه بر این، V t نشان‌دهنده میانگین سرعت پس‌زمینه در صفحه مماسی است در حالی که Vn مولفه میانگین سرعت پس‌زمینه در جهت عادی است . | اگرچه عدد موج خارج از صفحه kz نامیده می‌شود ، اما سطح دو بعدی که معادله 12-5 بر روی آن تعریف شده است، لزوماً برای هندسه‌های سه‌بعدی نباید نسبت به محور z نرمال باشد . |
