 |
جریان دو فازی در محیط متخلخل: مدل باکلی-لورت
معرفی
این مثال از رابط چند فازی چندفازی در رسانه متخلخل برای مدلسازی فرآیند جابجایی غیرقابل امتزاج در یک محیط متخلخل استفاده می‌کند. می توانید به جابجایی نفت توسط آب در یک مخزن فکر کنید. در یک محیط تک بعدی و تحت مفروضات معین، معادلات اشباع و فشار دو فاز به یک معادله حفاظتی برای اشباع یکی از فازها، معادله باکلی-لورت، کاهش می‌یابد. در تنظیم مدلی که در زیر توضیح داده شده است، این معادله امکان یک راه حل تحلیلی را فراهم می کند، و به این ترتیب، این مثال به عنوان یک مدل معیار نیز عمل می کند.
تعریف مدل
یک محیط متخلخل 1 بعدی با طول 1 متر در نظر گرفته می شود. فرض بر این است که هر دو فاز موجود تراکم ناپذیر هستند، هیچ منبع یا فرورفتگی وجود ندارد، و گرانش هیچ نقشی ندارد. علاوه بر این، فشار مویرگی صفر و نفوذپذیری (نسبی) و تخلخل مستقل از زمان و مکان در نظر گرفته شده است.
در ابتدا محیط متخلخل به طور کامل با فاز 1 پر می شود. در x = 0 فاز 2 با شار حجمی 0.001 m/s وارد محیط متخلخل می شود و فاز 1 را جابجا می کند که اجازه می دهد در x = 1 از حوزه متخلخل خارج شود. شار حجمی فاز 1 برابر با 0 در x = 0 است. فشار در x = 1 برابر با 0 Pa تنظیم شده است. جدول 1 خواص مواد مربوطه را جمع آوری می کند. این فرآیند در بازه زمانی 300 ثانیه شبیه سازی شده است.
از مفروضات و شرایط مرزی ذکر شده در بالا، نتیجه می شود که شار حجمی کل u = u 1 + u 2 در زمان و مکان ثابت است و معادلات جریان دو فازی که در رابط جریان چند فازی در محیط متخلخل برای اشباع و فشارها به یک معادله برای اشباع s 1 کاهش می یابد
(1)
که در آن ε p نشان دهنده تخلخل و λi =κ r i / μi است ، با κr i و μi به ترتیب نفوذپذیری نسبی و ویسکوزیته دینامیکی فاز i است. این معادله امکان حل تحلیلی را فراهم می کند ( برای ساختن حل تحلیلی این معادله باکلی-لورت به رفر. 1 مراجعه کنید). در بخش نتایج و بحث زیر، حل تحلیلی معادله باکلی-لورت با حل به دست آمده با جریان چند فازی در رابط رسانه متخلخل مقایسه شده است.
تعداد | ارزش | شرح |
ρ 1 = ρ 2 | 1000 کیلوگرم بر متر مکعب | چگالی هر دو فاز |
μ 1 = μ 2 | 0.001 کیلوگرم/(متر·ثانیه) | ویسکوزیته دینامیکی هر دو فاز |
ε ص | 0.5 | تخلخل |
ک | 10 -9 متر مربع _ | نفوذپذیری |
k r1 | s 1 2 | نفوذپذیری نسبی فاز 1 |
κ r2 | s 2 2 | نفوذپذیری نسبی فاز 2 |
نتایج و بحث
در شکل 1 پروفیل های اشباع s 2 برای نمونه های مختلف در زمان نشان داده شده است (فاصله های 20 ثانیه). فاز 1 توسط فاز 2 جابه جا می شود و محلول شوکی را نشان می دهد که از ناحیه متخلخل عبور می کند. حل معادلات جریان دو فازی (خطوط جامد) تطابق خوبی با حل تحلیلی معادله باکلی-لورت در معادله 1 (خطوط نقطه‌دار) نشان می‌دهد.
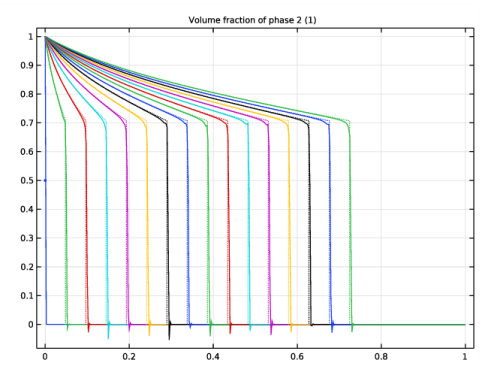
شکل 1: پروفایل های اشباع برای فاز 2 در فواصل 20 ثانیه نشان داده شده است، همانطور که با استفاده از جریان چند فازی در رابط رسانه متخلخل (خطوط جامد) محاسبه می شود، و به صورت تحلیلی به عنوان حل معادله باکلی-لورت به دست می آید.
ارجاع
1. R. Helmig، جریان چند فازی و فرآیندهای حمل و نقل در زیر سطح – سهمی در مدلسازی سیستم‌های آبی ، Springer-Verlag، 1997.
مسیر کتابخانه برنامه: Subsurface_Flow_Module /Verification_Examples/buckley_leverett_model
دستورالعمل مدلسازی
از منوی File ، New را انتخاب کنید .
جدید
در پنجره جدید ، روی 
Model Wizard کلیک کنید .
Model Wizard کلیک کنید .مدل جادوگر
1 | در پنجره Model Wizard ، روی  1D کلیک کنید . |
2 | در درخت انتخاب فیزیک ، جریان سیال > رسانه متخلخل و جریان زیرسطحی > جریان چند فاز در محیط متخلخل را انتخاب کنید . |
3 | روی افزودن کلیک کنید . |
4 |  روی مطالعه کلیک کنید . |
5 | در درخت انتخاب مطالعه ، General Studies>Time Dependent را انتخاب کنید . |
6 |  روی Done کلیک کنید . |
هندسه 1
فاصله 1 (i1)
در پنجره Model Builder ، در قسمت Component 1 (comp1) روی Geometry 1 کلیک راست کرده و Interval را انتخاب کنید .
برای تجسم حل تحلیلی معادله باکلی-لورت و مقایسه آن با حل محاسبه شده با استفاده از جریان چند فازی در رابط متخلخل، یک تابع تحلیلی تکه ای اضافه کنید.
تعاریف
تکه ای 1 (pw1)
1 | در نوار ابزار Home ، روی  Functions کلیک کنید و Local>Piecewise را انتخاب کنید . |
2 | در پنجره تنظیمات برای Piecewise ، قسمت Definition را پیدا کنید . |
3 | زیربخش فواصل را پیدا کنید . در جدول تنظیمات زیر را وارد کنید: |
شروع کنید | پایان | تابع |
0.7071 | 1 | d(x^2/(x^2+(1-x)^2)،x) |
انتقال فاز در محیط متخلخل (PHTR)
خواص انتقال فاز و متخلخل رسانه 1
1 | در پنجره Model Builder ، در قسمت Component 1 (comp1)>Phase Transport in Porous Media (phtr) روی Phase and Porous Media Transport Properties 1 کلیک کنید . |
2 | در پنجره تنظیمات برای ویژگی های انتقال رسانه فاز و متخلخل ، بخش خصوصیات فاز 1 را پیدا کنید . |
3 | از لیست ρ s1 ، User defined را انتخاب کنید . از لیست μ s1 ، User defined را انتخاب کنید . قسمت Phase 2 Properties را پیدا کنید . از لیست ρ s2 ، User defined را انتخاب کنید . از لیست μ s2 ، User defined را انتخاب کنید . این دانسیته و ویسکوزیته دینامیکی هر دو فاز را روی مقادیر پیش‌فرض ρ = 1000 kg/m3 و μ = 10-3 Pa ·s تنظیم می‌کند. |
کسری جلدی 1
1 | در نوار ابزار Physics ، روی  Boundaries کلیک کنید و Volume Fraction را انتخاب کنید . |
2 | فقط مرز 1 را انتخاب کنید. |
3 | در پنجره تنظیمات Volume Fraction ، بخش Volume Fraction را پیدا کنید . |
4 | کادر Phase s2 را انتخاب کنید . |
5 | در قسمت متنی s 0,s2 ، 1 را تایپ کنید . |
خروجی 1
1 | در نوار ابزار Physics ، روی  Boundaries کلیک کنید و Outflow را انتخاب کنید . |
2 | فقط مرز 2 را انتخاب کنید. |
قانون دارسی (DL)
ماتریس متخلخل 1
1 | در پنجره Model Builder ، در قسمت Component 1 (comp1)> Darcy’s Law (dl)> Porous Medium 1 روی Porous Matrix 1 کلیک کنید . |
2 | در پنجره تنظیمات برای ماتریس متخلخل ، بخش ویژگی های ماتریس را پیدا کنید . |
3 | از لیست ε p ، User defined را انتخاب کنید . در قسمت متن مرتبط، 0.5 را تایپ کنید . |
4 | از لیست κ ، User defined را انتخاب کنید . در قسمت متن مرتبط، 1e-9[m^2] را تایپ کنید . |
ورودی 1
1 | در نوار ابزار Physics ، روی  Boundaries کلیک کنید و Inlet را انتخاب کنید . |
2 | فقط مرز 1 را انتخاب کنید. |
3 | در پنجره تنظیمات برای ورودی ، بخش Velocity را پیدا کنید . |
4 | در قسمت متنی U 0 ، 0.001 را تایپ کنید . |
فشار 1
1 | در نوار ابزار Physics ، روی  Boundaries کلیک کنید و Pressure را انتخاب کنید . |
2 | فقط مرز 2 را انتخاب کنید. |
مش 1
لبه 1
در نوار ابزار Mesh ، روی Edge کلیک کنید .
Edge کلیک کنید .توزیع 1
1 | روی Edge 1 کلیک راست کرده و Distribution را انتخاب کنید . |
2 | در پنجره تنظیمات برای توزیع ، بخش توزیع را پیدا کنید . |
3 | در فیلد متنی Number of element ، 400 را تایپ کنید . |
مطالعه 1
مرحله 1: وابسته به زمان
1 | در پنجره Model Builder ، در بخش مطالعه 1 ، روی Step 1: Time Dependent کلیک کنید . |
2 | در پنجره تنظیمات مربوط به زمان وابسته ، قسمت تنظیمات مطالعه را پیدا کنید . |
3 | در قسمت متن زمان خروجی ، range(0,20,300) را تایپ کنید . |
راه حل 1 (sol1)
1 | در نوار ابزار مطالعه ، روی  Show Default Solver کلیک کنید . |
2 | در پنجره Model Builder ، گره Solution 1 (sol1) را گسترش دهید . |
3 | در پنجره Model Builder ، در قسمت Study 1>Solver Configurations>Solution 1 (sol1) روی Time-Dependent Solver 1 کلیک کنید . |
4 | در پنجره تنظیمات برای حل وابسته به زمان ، برای گسترش بخش Time Steping کلیک کنید . |
5 | از لیست مراحل انجام شده توسط حل کننده ، Strict را انتخاب کنید . |
6 | زیربخش تنظیمات متغیر جبری را پیدا کنید . از لیست تخمین خطا ، Exclude algebraic را انتخاب کنید . |
7 |  روی محاسبه کلیک کنید . |
نتایج
کسر حجمی (phtr)
دو نمودار پیش فرض به طور خودکار ایجاد می شود – یکی برای کسر حجمی و دیگری برای توزیع فشار. نموداری از محلول تحلیلی را به شکل زیر به نمودار کسر حجمی اضافه کنید.
1 | در پنجره تنظیمات برای گروه طرح 1 بعدی ، برای گسترش بخش عنوان کلیک کنید . |
2 | از لیست نوع عنوان ، دستی را انتخاب کنید . |
3 | در قسمت متن عنوان ، کسر حجمی فاز 2 (1) را تایپ کنید . |
نمودار خط 2
1 | روی Volume Fraction (phtr) کلیک راست کرده و Line Graph را انتخاب کنید . |
2 | فقط دامنه 1 را انتخاب کنید. |
3 | در پنجره تنظیمات برای نمودار خط ، بخش y-Axis Data را پیدا کنید . |
4 | در قسمت Expression text، x را تایپ کنید . |
5 | قسمت x-Axis Data را پیدا کنید . از لیست Parameter ، Expression را انتخاب کنید . |
6 | در قسمت متن Expression ، pw1(x)*(0.001*t)/0.5 را تایپ کنید . |
7 | برای گسترش بخش Coloring and Style کلیک کنید . زیربخش Line style را پیدا کنید . از لیست خط ، نقطه نقطه را انتخاب کنید . |
8 | از فهرست رنگ ، چرخه (بازنشانی) را انتخاب کنید . |
9 | در نوار ابزار Volume Fraction (phtr) ، روی  Plot کلیک کنید و با شکل 1 مقایسه کنید . |
