فرمول بندی شرایط مرزی به صورت کلی ( معادله 1-16 ) و شکل ضریب ( معادله 2-16 ) هر دو شرایط دیریکله و نویمان را همزمان تحمیل می کند:
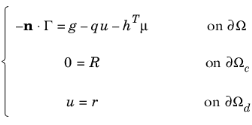
که در آن Γ بردار شار است ( Γ = – c ∇ u -α u + γ برای معادله شکل ضریب) و δΩc و δΩ d بخشهایی از مرز کلی هستند، δΩ ، که در آن محدودیتهای کلی و شرایط دیریکله مشخص شدهاند. ترکیب شرایط انواع مختلف در یک مرز ممکن است به دلیل یک متغیر وابسته جدید μ ، که فقط بر روی مرز تعریف شده است. این متغیر ناشناخته μ ضریب لاگرانژ نامیده می شود و معمولاً تفسیر فیزیکی دارد. به عنوان مثال، در مسائل مکانیک سازه، ضریب لاگرانژ برابر با نیروهای واکنش روی مرز است.
ضریب h T در شرایط مرزی نیومن نیروی محدودیت ژاکوبین است . این تصمیم میگیرد که ضربکنندههای لاگرانژ که محدودیت را اعمال میکنند چگونه مقیاسبندی و بر روی معادلات توزیع شوند. تنظیمات پیش فرض در گره محدودیت استفاده می شود
در حالی که یک گره شرط مرزی دیریکله به طور پیش فرض با h T = – 1 مطابقت دارد . مثلا:
|
•
|
شرط دیریکله u = r است و تنظیمات محدودیت پیشفرض به معنی h T = – 1 است . شرط نویمان به صورت زیر می شود:
|
ضریب لاگرانژ، μ ، طوری تنظیم می شود که شرایط دیریکله درخواستی را برآورده کند. تعیین یک غیرصفر g مقدار ضریب لاگرانژ را در همان مرز تغییر می دهد اما جواب واقعی u را تحت تأثیر قرار نمی دهد . بنابراین، این معادله را معمولاً می توان نادیده گرفت و به طور موثر یک شرط دیریکله خالص باقی گذاشت.
|
•
|
وقتی هیچ محدودیتی روی یک مرز اعمال نمی شود، مقدار R صفر است، یا معادل آن، شرط دیریکله 0 = 0 است . بنابراین h T صفر است و شرط نیومن:
|
این حالت تعمیم یافته نیومن بدون ضریب لاگرانژ است.
|
|
|
مثال: سیستم دو متغیر به شکل کلی
مثال زیر تعدادی از ترکیبهای شرایط مرزی ممکن را برای یک سیستم ثابت با دو متغیر وابسته u 1 و u 2 و دو قید نشان میدهد که شرایط واکنش به طور متقارن در تمام فیزیک اعمال میشود. این پیاده سازی پیش فرض و مفیدترین است. به شکل کلی نوشته شده است:
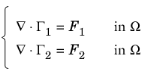
با شرایط مرزی پیش فرض نویمان
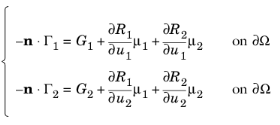
نوشتن کاربرد متقارن شرایط واکنش بر روی همه متغیرهای وابسته و شرایط مرزی دیریکله:
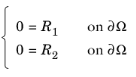
مجموعه یکسانی از شرایط مرزی در تمام رابط های PDE قابل دسترسی است. برای نشان دادن انعطاف پذیری شرط مرزی محدودیت R = 0 ، این موارد را در نظر بگیرید:
مورد 1:
اجازه دهید R 1 = R 2 = 0 . سپس شرایط مرزی دیریکله 0 = 0 را می دهد . علاوه بر این، اصطلاحات حاوی ضرب کننده های لاگرانژ از شرایط مرزی نویمان ناپدید می شوند. بنابراین شما فقط شرایط مرزی نویمان را دارید:
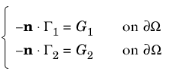
مورد 2:
فرض کنید R 1 = r 1 − u 1 و R 2 = r 2 − u 2 . سپس شرایط دیریکله همان u 1 = r 1 و u 2 = r 2 است . با استفاده از تنظیمات پیشفرض برای شرایط واکنش محدودیت،
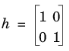
و شرایط مرزی نویمان تبدیل می شود:
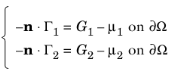
این معادلات آخر هیچ محدودیتی بر u 1 یا u 2 اعمال نمی کند ، زیرا ضرب کننده های لاگرانژ μ 1 و μ 2 همیشه طوری تنظیم می شوند که شرایط دیریکله را برآورده کنند. در این مورد، شرایط مرزی نویمان را نادیده بگیرید.
مورد 3:
فرض کنید R 1 = r 1 − u 1 و R 2 = 0 . سپس شرایط دیریکله است
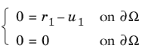
و شرایط پیش فرض نیومن از جمله شرایط واکنش عبارتند از:
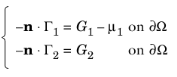
اولین شرط نویمان را می توان نادیده گرفت زیرا هیچ محدودیتی بر u 1 یا u 2 اعمال نمی کند . شما عملاً فقط شرط دیریکله در u 1 را همراه با شرط دوم نویمان دارید.
مورد 4:
مانند مورد 3 اما با دو PDE که با هم عوض شده اند ( Γ 1 و Γ 2 و همچنین F 1 و F 2 ). سپس PDE ها عبارتند از:
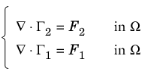
شرط دیریکله مشابه حالت 3 است: u 1 = r 1 . به طور پیش فرض، شرایط نویمان به صورت زیر در می آید:
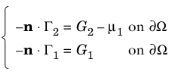
به طور موثر، شما فقط شرط نیومن را دارید – n · Γ 1 = G 1 . در مقایسه با مورد 3، شرایط PDE و دیریکله یکسان است، در حالی که شرایط نویمان متفاوت است. هر دو شرایط دیریکله و نویمان اکنون روی u 1 اعمال می شوند و هیچ چیزی برای u 2 مشخص نشده است .
|
|
این مثال نشان میدهد که هنگام اختلاط شرایط دیریکله و نویمان در PDEهای فرم ضریب و PDEهای فرم عمومی، ترتیب معادلات و متغیرهای وابسته مهم هستند. با این حال، ترتیب شرایط دیریکله اهمیتی ندارد زیرا ضریب های مختلف لاگرانژ برای همه اهداف عملی از یکدیگر قابل تشخیص نیستند.
|
مورد 5:
در نهایت، اجازه دهید R 1 = u 2 − u 1 و R 2 = 0 . همچنین فرض کنید که u 1 و u 2 در دو دامنه مجاور به جای یک دامنه وجود دارند. بردارهای نرمال همانطور که از دو طرف دیده می شوند n 1 = – n 2 = n هستند . سپس شرایط دیریکله عبارتند از:
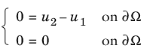
و شرایط نویمان با استفاده از شرایط واکنش متقارن پیش فرض عبارتند از:
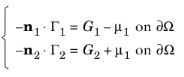
همان ضریب لاگرانژ اکنون در هر دو شرایط نویمان ظاهر می شود، که می تواند تعاریف متفاوتی از Γ و G داشته باشد . بنابراین، بر خلاف موارد 2 و 3، شرایط نویمان را نمی توان نادیده گرفت. در عوض، با افزودن این دو شرط، مشخص میشود که راهحل و شار روی مرز باید برآورده شوند:
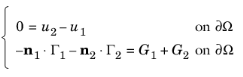
به طور خاص، اگر G 1 = G 2 = 0 ، آخرین شرط ساده می شود:
این بدان معنی است که هر دو متغیر u 1 و u 2 و شارهای مربوطه در مرز برابر هستند. اگر u 1 و u 2 یک مقدار را نشان دهند، این همان شرایط پیوستگی است که به طور ضمنی در هر مرز عنصر مش در مدل وجود دارد، جایی که هیچ چیز دیگری مشخص نشده است.
|
|
در همه این مثال ها، مقادیر ضرب کننده های لاگرانژ اهمیتی ندارند. با این حال، آنها اغلب دارای اهمیت فیزیکی هستند. در مکانیک سازه، اصطلاح h T μ در شرایط نیومن، نیروی واکنش لازم برای برآورده کردن محدودیتهای سینماتیکی توصیفشده توسط شرایط دیریکله است.
|




