 |
تشدید کننده هلمهولتز با حل کننده های دامنه فرکانس های مختلف تجزیه و تحلیل شد
معرفی
این مثال یک تشدیدگر سه بعدی متقارن محوری هلمهولتز را شبیه‌سازی می‌کند، یک مدل کلاسیک آکوستیک از مدار تشدید کننده با یک راه‌حل نظری شناخته شده. نسخه ایده آل در نظر گرفته شده در اینجا شامل یک لوله و یک حجم بسته به صورت سری است که در معرض فشار نوسانی هماهنگ هستند. پدیده‌های دنیای واقعی که توسط تشدیدکننده توضیح داده می‌شوند، از جمله، رزونانس ناشی از دمیدن در بالای بطری خالی و صدای تولید شده توسط درام‌های حفره‌ای بسته مانند djembe و ساب ووفرها هستند. این مدل استفاده از حل کننده های عددی مختلف را نشان می دهد. این مدل نشان می‌دهد که چگونه می‌توان این مشکل آکوستیک فشار را برای طیف وسیعی از فرکانس‌ها با استفاده از حل‌کننده‌های زیر حل کرد: (الف) دامنه فرکانس، با و بدون ارزیابی شکل موج مجانبی (AWE) برای حل سریع‌تر، و (ب) دامنه فرکانس – مدال،
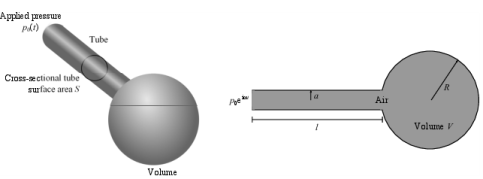
شکل 1: تصاویر تشدید کننده هلمهولتز.
تعریف مدل
این مدل شامل یک لوله و حجم است که به صورت سری به هم متصل شده اند که توسط فشار نوسانی هماهنگ p 0 ( t ) = p 0 e i ω t در ورودی لوله هدایت می شود. تشدید کننده هلمهولتز (به صورت شماتیک در شکل 1 نشان داده شده است ) یکی از ساده ترین مدارهای تشدید کننده است. این مدار معمولاً با استفاده از مدلسازی با پارامتر توده‌ای (مدار معادل) توصیف می‌شود (به عنوان مثال، رفرنس 1 را ببینید ) به عنوان یک جفت سریال از اینرسی صوتی L (معادل اندوکتانس در مدارهای الکتریکی و جرم در مکانیک نقطه جرم) ایجاد می‌شود. با شتاب مایع در لوله و انطباق صوتی C(معادل ظرفیت در مدارهای الکتریکی و فنر در مکانیک نقطه جرم) ناشی از فشرده سازی حجم. شکل 1 و شکل 3 را ببینید .
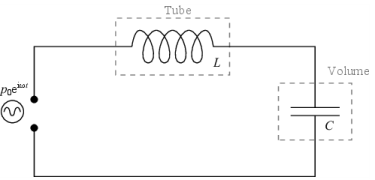
شکل 2: نمودار مدار الکتریکی معادل تشدید کننده هلمهولتز.
از آنجایی که فشرده‌سازی حجم سیال و شتاب سیال در لوله، رویدادهای آنی نیستند، بلکه در مقیاس‌های زمانی خاصی رخ می‌دهند (که هر کدام توسط هندسه همراه با ویژگی‌های سیال ارائه می‌شود)، پاسخ تشدیدگر به فرکانس بستگی دارد. و فرکانسی وجود دارد که پاسخ را به حداکثر می رساند – به عبارت دیگر، فرکانس تشدید ω R . البته با توجه به تشابه مستقیم مدارهای LC الکتریکی، این قابل انتظار است ، و با همان قیاس متوجه می شویم که فرکانس تشدید توسط
(1)
همانطور که در Ref. 1 ، المان های پارامتری انبوه آکوستیک توسط داده می شوند
(2)
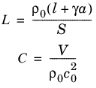
که ρ 0 چگالی خاموش پس زمینه سیال است، c 0 سرعت خاموش پس زمینه صوت، l طول لوله، a شعاع لوله، S سطح مقطع لوله عرضی به جهت جریان، γ ضریب تصحیح انتهایی (به تفصیل در زیر)، و V حجم بسته است. بنابراین، با استفاده از معادله 2 در معادله 1 ، متوجه می شویم که فرکانس تشدید ω R توسط
(3)
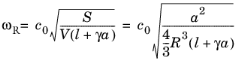
که در آخرین معادله فرض کرده ایم که حجم یک کره است 
و لوله استوانه ای است بنابراین S = π a 2 .
و لوله استوانه ای است بنابراین S = π a 2 .ضریب تصحیح پایان γ : منشا فیزیکی و مقدار عددی تقریبی
هنگامی که مایع از لوله خارج می شود و وارد حجم می شود، امواج صوتی پراکنده شده و فشار صوتی کاهش می یابد. با این حال، امواج در ابتدا در امتداد محور لوله زمانی که فقط آن را ترک می‌کنند ادامه می‌یابند و علاوه بر این، نمی‌توانند به منطقه اشغال شده توسط لوله حرکت کنند. در نتیجه، با خروج از لوله بلافاصله به طور کامل پراکنده نمی شوند و منطقه مستقیم پایین دست لوله همچنان توسط مایع درون لوله که بار صوتی را تحمیل می کند، احساس می شود. در مدل‌های ایده‌آل، این بار منجر به یک اینرسی صوتی اضافی می‌شود که مربوط به افزایش مؤثر طول لوله توسط γa است . به عبارت دیگر، طول کل اینرسی پارامتر یکپارچه L در معادله 2 بیشتر از طول لوله واقعی l است.
ضریب γ به هندسه خاص اتصال لوله-حجم بستگی دارد و از درجه وحدت است، Ref. 1 و 2 . ما باید یک فلنج بی نهایت را به عنوان مرجع در نظر بگیریم که ضریب تصحیح آن γ = 0.82 است ( مراجعه 2 ). این کاملاً صحیح نیست زیرا فشار صوتی کمتر در هندسه دایره ای پراکنده می شود که منجر به بار صوتی بزرگتر می شود.
توضیحات حل کننده
با استفاده از تنظیمات پیش‌فرض برای حل‌کننده دامنه فرکانس، مشکلی را که در معرض تحریک هارمونیک در مجموعه‌ای از فرکانس‌های تحریک مشخص شده است، حل می‌کند. در حالی که این می تواند برای جاروهای فرکانس بزرگتر زمان بر باشد، راه حل دقیق (از لحاظ عددی) به صراحت در هر فرکانس محاسبه می شود، و بنابراین همیشه می توان انتظار داشت که راه حل های این حل کننده صحیح باشند (با فرض همگرایی مدل و مش بندی مناسب برای حل تمام مقیاس های طولی فیزیک).
برای جابجایی های بزرگتر، این حل کننده همچنین دارای گزینه ای برای اعمال ارزیابی شکل موج مجانبی (AWE) است. این رویکرد به طور صریح جواب دقیق را در همه فرکانس ها محاسبه نمی کند، اما در عوض یک بسط تیلور از راه حل را در مورد چند راه حل دقیق انجام می دهد و در غیر این صورت از تقریب مرتبه پایین تر (پاده یا تیلور) برای تخمین راه حل در محدوده فرکانس مورد نیاز استفاده می کند.
در نهایت، حل کننده Frequency Domain Modal نیز می تواند برای انجام یک جابجایی فرکانس استفاده شود. برای این کار، ابتدا مجموعه‌ای از فرکانس‌های ویژه سیستم و حالت‌های ویژه مرتبط را محاسبه می‌کند (جستجو در محدوده تعریف‌شده توسط کاربر یا تعداد فرکانس‌های تعریف‌شده توسط کاربر). سپس راه‌حل کامل در جاروب فرکانس با یک ترکیب خطی از مجموعه پایه که توسط راه حل‌های ویژه تشکیل شده است، تقریب می‌یابد (نگاه کنید به یادداشت‌هایی درباره پیاده‌سازی COMSOL ).
اهداف تحلیل
این مشکل آکوستیک فشار در یک رژیم فرکانس مشخص با استفاده از حل‌کننده‌های مختلف، با هدف دوگانه نشان دادن قابلیت‌های حل‌کننده‌ها و همچنین برجسته کردن تنظیمات خاص حل‌کننده، حل می‌شود. حل‌کننده‌های از پیش تعیین‌شده زیر استفاده می‌شوند: (الف) دامنه فرکانس، با و بدون ارزیابی شکل موج مجانبی (AWE) برای حل سریع‌تر، و (ب) دامنه فرکانس مدال، که پاسخ فرکانسی را بر اساس فرکانس‌های ویژه در محدوده مشخص‌شده بازسازی می‌کند.
مقاومت در برابر تشعشعات صوتی
به عنوان نکته پایانی، لازم به ذکر است که نمودار مدار معادل در شکل 2 نادرست است. شرح مدار معادل کامل تشدید کننده همچنین باید شامل مقاومت تشعشع صوتی R ناشی از انرژی تلف شده از لوله در هنگام حرکت سیال در لوله به داخل حجم باشد، به شکل 3 مراجعه کنید . فرمول های ریاضی برای مقاومت در تعدادی از موقعیت ها را می توان در Ref. 1 . با این حال، مقدار مقاومت بر فرکانس رزونانس (تنها بازخوانی مورد استفاده در اینجا) تأثیر نمی‌گذارد، فقط بر سطح مطلق امپدانس سیستم تأثیر می‌گذارد، بنابراین ما به خوبی در نادیده گرفتن R .
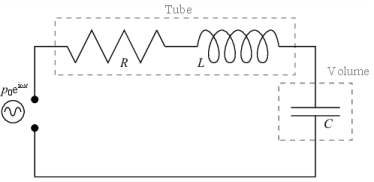
شکل 3: نمودار مدار الکتریکی معادل تشدید کننده هلمهولتز شامل مقاومت تابشی R.
نتایج و بحث
این مدل از فشار آکوستیک مطلق به‌طور میانگین بر روی حجم نهایی استفاده می‌کند
(4)
برای بررسی پاسخ ما متوجه می‌شویم که پایین‌ترین فرکانس ویژه در واقع با رزونانس پیش‌بینی‌شده توسط مدل پارامتر یکپارچه مطابقت دارد، و این پیش‌بینی نظری در واقع مطابقت خوبی با نتایج عددی دارد. با این حال، راه‌حل‌های کامل عددی COMSOL Multiphysics، بسیاری از حالت‌های بالاتر را نشان می‌دهند که در مدل ساده پارامترهای یکپارچه نادیده گرفته می‌شوند.
با مقایسه حل کننده های مختلف، اشاره می شود که همه آنها پاسخ یکسانی را برای جابجایی فرکانس ایجاد می کنند. شکل 4 و شکل 5 را به ترتیب در مقیاس های لگاریتمی و خطی ببینید . سطح فشار صوت در 1123.1 هرتز در شکل 6 نشان داده شده است . روش‌های جابجایی فرکانس مبتنی بر AWE و مدال برای سرعت بخشیدن به زمان‌های اجرای مدل‌های بزرگ با تعداد زیادی فرکانس درخواستی بسیار مفید هستند. به دلیل کم بودن درجه آزادی در این مدل، امکان اندازه گیری هیچ گونه افزایش سرعت در زمان CPU وجود ندارد. برای جزئیات بیشتر به بخش بعدی مراجعه کنید.
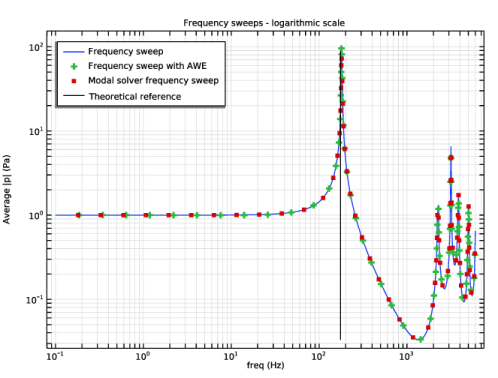
شکل 4: جابجایی فرکانس برای 
توافق تصویری بازخوانی بین همه حل‌کننده‌ها و نظریه برای اولین فرکانس ویژه و همچنین نشان دادن توافق بین همه حل‌کننده‌ها برای فرکانس‌های بالاتر.
توافق تصویری بازخوانی بین همه حل‌کننده‌ها و نظریه برای اولین فرکانس ویژه و همچنین نشان دادن توافق بین همه حل‌کننده‌ها برای فرکانس‌های بالاتر.
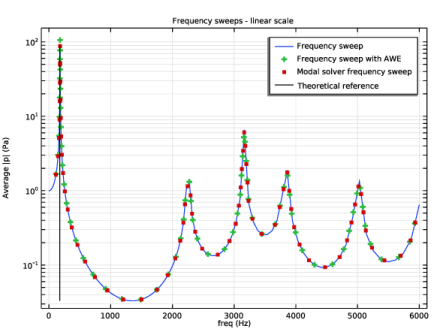
شکل 5: جابجایی فرکانس مشابه در شکل 4 که در اینجا در مقیاس فرکانس خطی نشان داده شده است تا بر فرکانس های بالاتر تأکید شود.
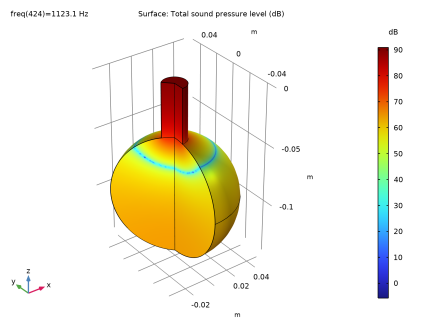
شکل 6: سطح فشار صدا که به عنوان خروجی پیش فرض از شبیه سازی ها محاسبه می شود، در اینجا برای f = 1123.1 هرتز نشان داده شده است.
نکاتی درباره پیاده سازی COMSOL
• | به عنوان یک قانون کلی، حداقل باید از پنج عنصر درجه دوم برای تفکیک هر طول موج استفاده شود. بنابراین، حداکثر اندازه عنصر مش روی 1/5 از کوتاه ترین طول موج های موجود، c_air / fmax تنظیم می شود . این اندازه مش به طور مصنوعی برای افزایش زمان اجرا تصفیه شده است. |
• | گزینه AWE به یک عبارت برای ارزیابی عملکرد حل کننده نیاز دارد (عبارت AWE). انتگرالی از فشار مطلق در کل سیستم استفاده می شود، اما سایر عملکردهای تعریف شده بر روی کل سیستم یا بخش هایی از آن نیز می توانند مورد استفاده قرار گیرند. |
• | هنگامی که چندین فرکانس رزونانس وجود دارد، پارامترهای پیش‌فرض برای گزینه AWE ممکن است از مقداری تنظیم استفاده کنند، برای مثال، با استفاده از یک مقدار تحمل مطلق کافی (به بخش >AWE Solver 1 مراجعه کنید ). در این مدل از مقدار پیش فرض 0.001 استفاده شده و نتایج معقولی (در مقایسه با روش های دیگر) به دست می دهد. کاهش مقدار به 0.0001 نتایج فرکانس بالا را اندکی بهبود می بخشد (نمودار مقیاس خطی را ببینید). سایر تنظیمات به طور کلی اهمیت کمتری دارند، مانند تغییر تعداد نقاط برای خطی کردن ( نقاط ارزیابی )، تغییر تعداد عبارت‌ها در بسط تیلور در مورد هر نقطه ( اندازه بسط )، یا تغییر از بسط Padé به بسط تیلور از راه حل تقریبی. ( نوع گسترش). در تنظیم فعلی، ما یک کران فرکانس بالایی نسبتاً بالا را انتخاب کردیم، بنابراین حدود 10 فرکانس رزونانس در جابجایی وجود دارد. اگر حد فرکانس بالایی کاهش یافته بود و تنها رزونانس اول گنجانده شده بود (به عنوان مثال، با تنظیم fmax = 100 هرتز)، آنگاه تحمل نسبی AWE پیش فرض کافی بود. توجه داشته باشید که اگر هر یک از انتهای محدوده فرکانس به یک رزونانس نزدیک باشد، حل کننده AWE می تواند غیرقابل اعتماد شود. |
• | عملگر linper به حل کننده اطلاع می دهد که عبارت در عبارت یک اغتشاش (یک عبارت منبع) است که باید در مسئله خطی شده گنجانده شود. حلگر مودال فقط از فشار زیر عملگر لاینپر به عنوان منبع استفاده می کند، در حالی که حل کننده های دیگر این عبارت اغتشاش را نادیده می گیرند. |
• | برای به دست آوردن نتایج خوب با حل‌کننده Modal تا fmax ، باید حد بالایی را در جستجوی فرکانس ویژه آن روی 1.5*fmax قرار دهیم تا حالت‌هایی را بگیریم که ممکن است بر بالاترین قسمت فرکانس مورد نظر تأثیر بگذارند. استفاده از fmax به عنوان حد بالایی منجر به تخمین ضعیف‌تر راه‌حل در فرکانس‌های بالاتر می‌شود. |
• | گزینه AWE و حل کننده Frequency Domain-Modal هر دو بر تقریب راه حل با استفاده از چند راه حل دقیق در محدوده sweep متکی هستند. بنابراین، این روش‌ها سرعت بیشتری را در زمان CPU ارائه می‌کنند، اگر تنها رزونانس‌های کمی در محدوده sweep قرار گیرند، یا اگر یافتن راه‌حل‌های ویژه نسبت به همه راه‌حل‌های کامل نسبتاً آسان‌تر باشد. بنابراین، این روش‌ها به‌ویژه برای مدل‌های بزرگ و جابجایی‌های فرکانس خوب در محدوده‌های وسیع مفید خواهند بود. حل جاروب فرکانس تقریباً 21 ثانیه طول می کشد، در حالی که حل کننده AWE به 12 ثانیه و جابجایی فرکانس مبتنی بر مودال فقط به 7 ثانیه نیاز دارد. افزایش سرعت به تعداد فرکانس های درخواستی و تعداد رزونانس های موجود در فرکانس مورد نظر بستگی دارد. |
• | در نهایت توجه داشته باشید که مدل را بر حسب پارامترهای هندسی ( a ، L و R ) تعریف می کنیم. این باعث می شود که به سرعت جابجایی های پارامتریک در هندسه گنجانده شود، که به عنوان مثال، می توان از آنها برای تنظیم پایین ترین فرکانس ویژه استفاده کرد. |
منابع
1. DT Blackstock, Fundamentals of Physical Acoustics , John Wiley & Sons, 2000.
2. AD Pierce، آکوستیک: مقدمه ای بر اصول و کاربردهای فیزیکی آن ، انجمن آکوستیکال آمریکا، 1989.
مسیر کتابخانه برنامه: ماژول_آکوستیک/آموزش_آکوستیک_فشار/حل‌کننده_رسوناتور_هلمهولتز
دستورالعمل مدلسازی
از منوی File ، New را انتخاب کنید .
جدید
در پنجره جدید ، روی 
Model Wizard کلیک کنید .
Model Wizard کلیک کنید .مدل جادوگر
1 | در پنجره Model Wizard ، روی  2D Axismetric کلیک کنید . |
2 | در درخت Select Physics ، Acoustics>Pressure Acoustics>Pressure Acoustics، Frequency Domain (acpr) را انتخاب کنید . |
3 | روی افزودن کلیک کنید . |
4 |  روی مطالعه کلیک کنید . |
5 | در درخت انتخاب مطالعه ، General Studies>Frequency Domain را انتخاب کنید . |
6 |  روی Done کلیک کنید . |
تعاریف جهانی
پارامترهای 1
بارگیری تمام پارامترهای مدل از یک فایل؛ اینها شامل پارامترهای هندسی و خصوصیات فیزیکی هوا است.
1 | در پنجره Model Builder ، در قسمت Global Definitions روی Parameters 1 کلیک کنید . |
2 | در پنجره تنظیمات برای پارامترها ، بخش پارامترها را پیدا کنید . |
3 |  روی Load from File کلیک کنید . |
4 | به پوشه Application Libraries مدل بروید و روی فایل helmholtz_resonator_solvers_parameters.txt دوبار کلیک کنید . |
هندسه 1
هندسه متقارن محور دوبعدی ساده تشدید کننده را از شکل 1 با استفاده از مستطیل ها و دایره ها بسازید.
مستطیل 1 (r1)
1 | در نوار ابزار Geometry ، روی  Rectangle کلیک کنید . |
شما با ساخت لوله شروع می کنید. طول L و شعاع a دارد .
2 | در پنجره تنظیمات برای Rectangle ، بخش Size and Shape را پیدا کنید . |
3 | در قسمت متن Width ، a را تایپ کنید . |
4 | در قسمت متن ارتفاع ، L را تایپ کنید . |
5 | قسمت Position را پیدا کنید . در قسمت متن z ، -L را تایپ کنید . |
دایره 1 (c1)
1 | در نوار ابزار Geometry ، روی  Circle کلیک کنید . |
ولوم را که شعاع Rv دارد و بعد از لوله قرار می گیرد را ادامه دهید. با دانستن اینکه لوله و حجم را در یک جسم (رزوناتور) ادغام خواهید کرد، از همپوشانی a/2 اطمینان حاصل می کنید. توجه داشته باشید که اشیاء یا قسمت‌هایی از اجسام که در سمت چپ خط تقارن ( r = 0) امتداد می‌یابند حذف خواهند شد، بنابراین نیازی نیست نیمه چپ دایره را به صورت دستی بردارید.
2 | در پنجره تنظیمات دایره ، بخش اندازه و شکل را پیدا کنید . |
3 | در قسمت متن Radius ، Rv را تایپ کنید . |
4 | قسمت Position را پیدا کنید . در قسمت متن z ، -(L+Rv-a/2) را تایپ کنید . |
اتحادیه 1 (uni1)
1 | در نوار ابزار Geometry ، روی  Booleans and Partitions کلیک کنید و Union را انتخاب کنید . |
قسمت های باقی مانده از هندسه را تمیز کنید.
2 | در پنجره Graphics کلیک کنید و سپس Ctrl+A را فشار دهید تا هر دو شی انتخاب شوند. |
حذف نهادهای 1 (del1)
1 | در پنجره Model Builder ، روی Geometry 1 کلیک راست کرده و Delete Entities را انتخاب کنید . |
2 | در شی uni1 فقط مرزهای 1، 2 و 5 را انتخاب کنید.  |
3 | در پنجره تنظیمات برای حذف نهادها ، روی  Build All Objects کلیک کنید . |
4 |  روی دکمه Zoom Extents در نوار ابزار Graphics کلیک کنید . |
5 | در نوار ابزار Geometry ، روی  ساختن همه کلیک کنید . |
مواد
حالا مواد را اضافه کنید. برای این مدل ساده، استفاده از مقادیر جدول بندی شده برای پارامترهای فیزیکی هوا کافی است، که می توان به صورت دستی با افزودن یک ماده خالی تعریف کرد و مقادیر rho_air و c_air را به آن اختصاص داد . یا هوا را از Material Library بارگیری کنید.
هوای من
1 | در پنجره Model Builder ، در قسمت Component 1 (comp1) روی Materials راست کلیک کرده و Blank Material را انتخاب کنید . |
2 | در پنجره تنظیمات برای مواد ، My air را در قسمت نوشتار Label تایپ کنید . |
3 | قسمت محتوای مواد را پیدا کنید . در جدول تنظیمات زیر را وارد کنید: |
ویژگی | متغیر | ارزش | واحد | گروه اموال |
تراکم | rho | rho_air | کیلوگرم بر متر مکعب | پایه ای |
سرعت صوت | ج | c_air | ام‌اس | پایه ای |
سپس متغیرهای یکپارچه و عملیات ادغام را تعریف کنید. ابتدا یک جفت ادغام را تعریف کنید که در حجم V ادغام می شود و برای ارزیابی پاسخ سیستم در بالای 1 استفاده می شود . سپس میانگین فشار مطلق را در حجمی که به عنوان بازخوانی پاسخ سیستم استفاده می شود، تعریف کنید.
تعاریف
ادغام 1 (در اول)
1 | در نوار ابزار تعاریف ، روی  Nonlocal Couplings کلیک کرده و Integration را انتخاب کنید . |
2 | فقط دامنه 1 را انتخاب کنید. |
متغیرهای 1
1 | در پنجره Model Builder ، روی Definitions کلیک راست کرده و Variables را انتخاب کنید . |
2 | در پنجره تنظیمات برای متغیرها ، بخش متغیرها را پیدا کنید . |
3 |  روی Load from File کلیک کنید . |
4 | به پوشه Application Libraries مدل بروید و روی فایل helmholtz_resonator_solvers_variables.txt دوبار کلیک کنید . |
آکوستیک فشار، دامنه فرکانس (ACPR)
آکوستیک فشار 1
در مرحله بعد، شما تعریف می کنید که آکوستیک فشار را در کل دامنه حل می کنید و شرایط مرزی را اعمال می کنید.
1 |  روی دکمه Zoom Extents در نوار ابزار Graphics کلیک کنید . |
فشار 1
1 | در پنجره Model Builder ، روی Pressure Acoustics، Frequency Domain (acpr) کلیک راست کرده و Pressure را انتخاب کنید . |
2 | فقط مرز 3 را انتخاب کنید. |
فشار اعمال شده ترکیبی از یک قطعه ثابت و یک اپراتور لاینپر است . قسمت ثابت در مراحل دامنه فرکانس و در بقیه غیرفعال خواهد بود، در حالی که قسمت لاینپر هنگام اجرای دامنه فرکانس، مرحله مدال فعال و در بقیه موارد غیرفعال خواهد بود، همانطور که در یادداشت ها درباره پیاده سازی COMSOL توضیح داده شده است.
3 | در پنجره تنظیمات فشار ، قسمت فشار را بیابید . |
4 | در قسمت متنی p 0 ، 1+linper(1) را تایپ کنید . |
مش
با استفاده از قابلیت مش کنترل شده توسط Physics، مش را ادامه داده و تولید کنید . فرکانس کنترل کننده حداکثر اندازه عنصر به صورت دستی وارد می شود تا حل کننده های مختلف مورد استفاده را در خود جای دهد. به طور کلی، 5 تا 6 عنصر درجه دوم در هر طول موج برای حل امواج مورد نیاز است. برای جزئیات بیشتر، مش بندی (رفع امواج) را در راهنمای کاربر ماژول آکوستیک ببینید . گزینه پیش فرض Automatic 5 عنصر در هر طول موج می دهد. در این مورد، ما از یک اندازه مش 8 برابر ریزتر برای افزایش مصنوعی زمان اجرا و نشان دادن تفاوت در زمان اجرا با حل کننده های مختلف استفاده می کنیم.
مش 1
1 | در پنجره Model Builder ، در قسمت Component 1 (comp1) روی Mesh 1 کلیک کنید . |
2 | در پنجره تنظیمات مش ، بخش آکوستیک فشار ، دامنه فرکانس (acpr) را پیدا کنید . |
3 | از فهرست پارامترهای کنترل اندازه عنصر حداکثر مش ، فرکانس را انتخاب کنید . |
4 | در قسمت متن f max ، fmax را تایپ کنید . |
5 | از لیست تعداد عناصر مش در هر طول موج ، User defined را انتخاب کنید . |
6 | در قسمت متن، 40 را تایپ کنید . |
7 |  روی ساخت همه کلیک کنید . |
مطالعه 1 – جارو فرکانس
بعد، اولین مورد از سه حل کننده (حل کننده دامنه فرکانس) را تنظیم کنید. هنگامی که این تجزیه و تحلیل را شروع کردید، قبلاً این حل کننده (این مطالعه) را وارد کرده اید، بنابراین می توانید بلافاصله آن را تنظیم کنید.
1 | در پنجره Model Builder ، روی Study 1 کلیک کنید . |
2 | در پنجره تنظیمات برای مطالعه ، Study 1 – Frequency Sweep را در قسمت نوشتار Label تایپ کنید . |
3 | بخش تنظیمات مطالعه را پیدا کنید . تیک Generate defaults defaults را پاک کنید . |
مرحله 1: دامنه فرکانس
1 | در پنجره Model Builder ، در بخش مطالعه 1 – جستجوی فرکانس ، روی مرحله 1: دامنه فرکانس کلیک کنید . |
2 | در پنجره تنظیمات دامنه فرکانس ، بخش تنظیمات مطالعه را پیدا کنید . |
3 | در قسمت متن فرکانس ها ، 10^{range(log10(fmin),(log10(fmax)-(log10(fmin)))/499,log10(fmax))} را تایپ کنید . |
این دستور 500 فرکانس را در محدوده fmin – fmax انتخاب می‌کند که در یک محور لگاریتمی نشان داده می‌شود.
4 | در نوار ابزار صفحه اصلی ،  روی محاسبه کلیک کنید . |
ریشه
اکنون از همان حل کننده قبلی استفاده کنید، اما این بار با گزینه Asymptotic Waveform Evaluation (AWE). شما این کار را به عنوان یک مطالعه جداگانه انجام می دهید تا بتوانید این دو راه حل را با هم مقایسه کنید و بنابراین ابتدا یک مطالعه دامنه فرکانس جدید اضافه می کنید.
اضافه کردن مطالعه
1 | در نوار ابزار Home ، روی  Add Study کلیک کنید تا پنجره Add Study باز شود . |
2 | به پنجره Add Study بروید . |
3 | زیربخش مطالعات را پیدا کنید . در درخت انتخاب مطالعه ، General Studies>Frequency Domain را انتخاب کنید . |
4 | روی Add Study در نوار ابزار پنجره کلیک کنید . |
5 | در نوار ابزار Home ، روی  Add Study کلیک کنید تا پنجره Add Study بسته شود . |
مطالعه 2
مرحله 1: دامنه فرکانس
1 | در پنجره تنظیمات دامنه فرکانس ، بخش تنظیمات مطالعه را پیدا کنید . |
2 | در قسمت متن فرکانس ها ، 10^{range(log10(fmin),(log10(fmax)-(log10(fmin)))/499,log10(fmax))} را تایپ کنید . |
3 | برای گسترش بخش Study Extensions کلیک کنید . کادر بررسی استفاده از ارزیابی شکل موج مجانبی را انتخاب کنید . |
4 | در جدول تنظیمات زیر را وارد کنید: |
عبارات ارزیابی شکل موج مجانبی (AWE). |
comp1.p_avg |
این تابع در طول الگوریتم AWE برای ارزیابی عملکرد آن استفاده می شود. توابع دیگر، از جمله مقدار در یک نقطه در سیستم، نیز می تواند مورد استفاده قرار گیرد.
راه حل 2 (sol2)
1 | در نوار ابزار مطالعه ، روی  Show Default Solver کلیک کنید . |
2 | در پنجره Model Builder ، گره Solution 2 (sol2) را گسترش دهید ، سپس روی AWE Solver 1 کلیک کنید . |
3 | در پنجره تنظیمات برای AWE Solver ، بخش Tolerances را پیدا کنید . |
4 | در قسمت متنی Relative tolerance 0.005 را تایپ کنید . |
تحمل حل کننده AWE برای اطمینان از صحت نتایج کاهش می یابد.
5 | در پنجره Model Builder ، روی Study 2 کلیک کنید . |
6 | در پنجره تنظیمات برای مطالعه ، قسمت تنظیمات مطالعه را پیدا کنید . |
7 | تیک Generate defaults defaults را پاک کنید . |
8 | در قسمت نوشتار Label ، Study 2 – Frequency Sweep را با AWE تایپ کنید . |
9 | در نوار ابزار مطالعه ،  روی محاسبه کلیک کنید . |
اضافه کردن مطالعه
1 | در نوار ابزار مطالعه ، روی  Add Study کلیک کنید تا پنجره Add Study باز شود . |
2 | به پنجره Add Study بروید . |
3 | زیربخش مطالعات را پیدا کنید . در درخت انتخاب مطالعه ، مطالعات پیش‌فرض برای واسط‌های فیزیک انتخاب شده > دامنه فرکانس، مدال را انتخاب کنید . |
4 | روی Add Study در نوار ابزار پنجره کلیک کنید . |
5 | در نوار ابزار مطالعه ، روی  Add Study کلیک کنید تا پنجره Add Study بسته شود . |
سپس حل کننده سوم را راه اندازی می کنید. مطالعه مدال دامنه فرکانس.
مطالعه 3 – جاروب فرکانس حلگر معین
1 | در پنجره Model Builder ، روی Study 3 کلیک کنید . |
2 | در پنجره تنظیمات برای مطالعه ، قسمت تنظیمات مطالعه را پیدا کنید . |
3 | تیک Generate defaults defaults را پاک کنید . |
4 | در قسمت نوشتار Label ، Study 3 – Modal solver frequency sweep را تایپ کنید . |
مرحله 1: فرکانس ویژه
1 | در پنجره Model Builder ، در مطالعه 3 – جابجایی فرکانس حلگر معین ، روی مرحله 1: فرکانس ویژه کلیک کنید . |
2 | در پنجره تنظیمات برای Eigenfrequency ، قسمت Study Settings را پیدا کنید . |
3 | از فهرست روش جستجوی فرکانس ویژه ، منطقه را انتخاب کنید . |
سپس، حد بالایی قسمت واقعی فرکانس‌هایی را که می‌خواهید بررسی کنید، تغییر دهید تا مطمئن شوید که کل محدوده فرکانس fmin – fmax به درستی حل شده است.
4 | زیربخش منطقه جستجو را پیدا کنید . در قسمت بزرگ ترین قسمت متن واقعی ، 1.5*fmax را تایپ کنید . |
مرحله 2: دامنه فرکانس، مدال
1 | در پنجره Model Builder ، روی Step 2: Frequency Domain، Modal کلیک کنید . |
2 | در پنجره تنظیمات برای دامنه فرکانس ، مدال ، بخش تنظیمات مطالعه را پیدا کنید . |
3 | در قسمت متن فرکانس ها ، 10^{range(log10(fmin),(log10(fmax)-(log10(fmin)))/499,log10(fmax))} را تایپ کنید . |
4 | در نوار ابزار مطالعه ،  روی محاسبه کلیک کنید . |
نتایج
جاروهای فرکانس – مقیاس لگاریتمی
1 | در نوار ابزار صفحه اصلی ، روی  Add Plot Group کلیک کنید و 1D Plot Group را انتخاب کنید . |
سپس، نموداری از پاسخ سیستم را در تمام فرکانس‌های مورد بررسی اضافه می‌کنید.
2 | در پنجره تنظیمات برای گروه طرح 1 بعدی ، فرکانس sweeps – مقیاس لگاریتمی را در قسمت نوشتار برچسب تایپ کنید. |
جارو فرکانس
1 | روی Frequency sweeps – logarithmic scale کلیک راست کرده و Global را انتخاب کنید . |
2 | در پنجره تنظیمات برای جهانی ، بخش داده را پیدا کنید . |
3 | از فهرست مجموعه داده ، مطالعه 1 – فرکانس جارو کردن/راه حل 1 (sol1) را انتخاب کنید . |
4 | قسمت y-Axis Data را پیدا کنید . در جدول تنظیمات زیر را وارد کنید: |
اصطلاح | واحد | شرح |
p_avg | پا | فشار متوسط در حجم |
5 | در قسمت Label text، Frequency Sweep را تایپ کنید . |
جارو فرکانس با AWE
1 | در پنجره Model Builder ، روی Frequency sweeps – logarithmic scale کلیک راست کرده و Global را انتخاب کنید . |
2 | در پنجره تنظیمات برای جهانی ، Frequency Sweep را با AWE در قسمت نوشتار Label تایپ کنید . |
3 | قسمت Data را پیدا کنید . از فهرست مجموعه داده ، مطالعه 2 – جابجایی فرکانس با AWE/Solution 2 (sol2) را انتخاب کنید . |
4 | قسمت y-Axis Data را پیدا کنید . در جدول تنظیمات زیر را وارد کنید: |
اصطلاح | واحد | شرح |
p_avg | پا | فشار متوسط در حجم |
جاروب فرکانس حلگر معین
1 | روی Frequency sweeps – logarithmic scale کلیک راست کرده و Global را انتخاب کنید . |
2 | در پنجره تنظیمات برای جهانی ، Modal solver frequency sweep را در قسمت نوشتار Label تایپ کنید . |
3 | قسمت y-Axis Data را پیدا کنید . در جدول تنظیمات زیر را وارد کنید: |
اصطلاح | واحد | شرح |
p_avg | پا | فشار متوسط در حجم |
4 | قسمت Data را پیدا کنید . از فهرست مجموعه داده ، مطالعه 3 – جاروب فرکانس حلگر معین /راه حل 3 (sol3) را انتخاب کنید . |
مرجع نظری
1 | روی Frequency sweeps – logarithmic scale کلیک راست کرده و Global را انتخاب کنید . |
2 | در پنجره تنظیمات برای جهانی ، مرجع نظری را در قسمت متن برچسب تایپ کنید . |
3 | قسمت Data را پیدا کنید . از فهرست مجموعه داده ، مطالعه 1 – فرکانس جارو کردن/راه حل 1 (sol1) را انتخاب کنید . |
4 | قسمت y-Axis Data را پیدا کنید . در جدول تنظیمات زیر را وارد کنید: |
اصطلاح | واحد | شرح |
p_avg | پا | فشار متوسط در حجم |
5 | قسمت x-Axis Data را پیدا کنید . از لیست Parameter ، Expression را انتخاب کنید . |
6 | در قسمت متن Expression ، f_theo را تایپ کنید . |
7 |  روی دکمه x-Axis Log Scale در نوار ابزار Graphics کلیک کنید . |
8 |  روی دکمه y-Axis Log Scale در نوار ابزار Graphics کلیک کنید . |
9 | در نوار ابزار Frequency Sweeps – scale logarithmic ، روی  Plot کلیک کنید . |
جارو فرکانس
1 | در پنجره Model Builder ، روی Frequency Sweep کلیک کنید . |
2 | در پنجره تنظیمات برای جهانی ، برای گسترش بخش Coloring and Style کلیک کنید . |
اکنون سبک‌های نمودار را تغییر دهید و متون افسانه‌ای را به‌روزرسانی کنید تا نمودارهای مناسب ارائه از پاسخ سیستم محاسبه‌شده از همه حل‌کننده‌ها را تولید کنید. اینها شبیه شکل 3 و شکل 4 خواهند بود .
جارو فرکانس با AWE
1 | در پنجره Model Builder ، روی Frequency Sweep with AWE کلیک کنید . |
2 | در پنجره تنظیمات برای جهانی ، قسمت Coloring and Style را پیدا کنید . |
3 | زیربخش Line style را پیدا کنید . از لیست Line ، هیچکدام را انتخاب کنید . |
4 | زیربخش نشانگرهای خط را پیدا کنید . از لیست نشانگر ، علامت بعلاوه را انتخاب کنید . |
5 | از لیست موقعیت یابی ، Interpolated را انتخاب کنید . |
6 | در قسمت متن شماره ، 70 را تایپ کنید . |
جاروب فرکانس حلگر معین
1 | در پنجره Model Builder ، روی Modal Solver Frequency Sweep کلیک کنید . |
2 | در پنجره تنظیمات برای جهانی ، قسمت Coloring and Style را پیدا کنید . |
3 | زیربخش Line style را پیدا کنید . از لیست Line ، هیچکدام را انتخاب کنید . |
4 | زیربخش نشانگرهای خط را پیدا کنید . از لیست نشانگر ، نقطه را انتخاب کنید . |
5 | از لیست موقعیت یابی ، Interpolated را انتخاب کنید . |
6 | در قسمت متن شماره ، 72 را تایپ کنید . |
جاروهای فرکانس – مقیاس لگاریتمی
1 | در پنجره Model Builder ، روی Frequency Sweeps – logarithmic scale کلیک کنید . |
2 | در پنجره تنظیمات برای گروه طرح 1 بعدی ، برای گسترش بخش عنوان کلیک کنید . |
3 | از لیست نوع عنوان ، Label را انتخاب کنید . |
4 | قسمت Legend را پیدا کنید . از لیست موقعیت ، سمت چپ بالا را انتخاب کنید . |
5 | قسمت Plot Settings را پیدا کنید . |
6 | چک باکس x-axis label را انتخاب کنید . در فیلد متن مرتبط، فرک (Hz) را تایپ کنید . |
7 | کادر بررسی برچسب محور y را انتخاب کنید . در قسمت متن مربوطه، میانگین |p| را تایپ کنید (Pa) . |
8 | برای گسترش بخش عنوان کلیک کنید . در نوار ابزار Frequency Sweeps – scale logarithmic ، روی  Plot کلیک کنید . |
جارو فرکانس
1 | در پنجره Model Builder ، روی Frequency Sweep کلیک کنید . |
2 | در پنجره تنظیمات برای جهانی ، برای گسترش بخش Legends کلیک کنید . |
3 | از فهرست Legends ، Manual را انتخاب کنید . |
4 | در جدول تنظیمات زیر را وارد کنید: |
افسانه ها |
جارو فرکانس |
جارو فرکانس با AWE
1 | در پنجره Model Builder ، روی Frequency Sweep with AWE کلیک کنید . |
2 | در پنجره تنظیمات برای جهانی ، بخش Legends را پیدا کنید . |
3 | از فهرست Legends ، Manual را انتخاب کنید . |
4 | در جدول تنظیمات زیر را وارد کنید: |
افسانه ها |
جارو فرکانس با AWE |
جاروب فرکانس حلگر معین
1 | در پنجره Model Builder ، روی Modal Solver Frequency Sweep کلیک کنید . |
2 | در پنجره تنظیمات برای جهانی ، بخش Legends را پیدا کنید . |
3 | از فهرست Legends ، Manual را انتخاب کنید . |
4 | در جدول تنظیمات زیر را وارد کنید: |
افسانه ها |
جاروب فرکانس حلگر معین |
مرجع نظری
1 | در پنجره Model Builder ، روی مرجع نظری کلیک کنید . |
2 | در پنجره تنظیمات برای جهانی ، بخش Legends را پیدا کنید . |
3 | از فهرست Legends ، Manual را انتخاب کنید . |
4 | در جدول تنظیمات زیر را وارد کنید: |
افسانه ها |
مرجع نظری |
5 | قسمت Coloring and Style را پیدا کنید . از لیست رنگ ، سیاه را انتخاب کنید . |
جاروهای فرکانس – مقیاس خطی
1 | در پنجره Model Builder ، روی Frequency sweeps – logarithmic scale کلیک راست کرده و Duplicate را انتخاب کنید . |
2 |  روی دکمه x-Axis Log Scale در نوار ابزار Graphics کلیک کنید . |
3 | در پنجره تنظیمات برای گروه طرح 1 بعدی ، Frequency sweeps – linear scale را در قسمت نوشتار Label تایپ کنید . |
