 |
تشدید کننده حفره متقارن محوری
معرفی
در این مثال، فرکانس‌های تشدید و میدان‌های یک حفره متقارن محوری با استفاده از فرمول متقارن محوری دو بعدی که با ماژول RF یا ماژول اپتیک موج در دسترس است، به دست می‌آیند. سطح مقطع حفره مستطیل شکل است و دیوارها رسانای الکتریکی کامل (PEC) هستند. برای این هندسه، اعمال جداسازی متغیرها منجر به معادلات ماورایی برای فرکانس‌های ویژه می‌شود و بنابراین این مثال به عنوان معیاری برای فرمول‌بندی متقارن محوری دوبعدی عمل می‌کند. فرکانس‌های تشدید به‌دست‌آمده با COMSOL Multiphysics با حل‌های معادلات ماورایی 1 قسمت در 10 6 مطابقت دارد.، که تلورانس پیش فرض حل کننده مقدار ویژه است. این مدل همچنین نشان می‌دهد که راه‌حل‌های به‌دست‌آمده با استفاده از فرمول متقارن محوری دوبعدی می‌توانند حول محور z بچرخند تا یک راه‌حل سه‌بعدی به دست آید.
تعریف مدل
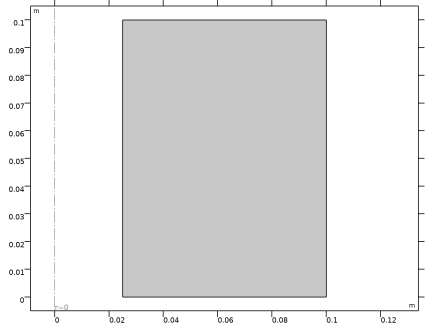
حفره متقارن محور با مقطع مستطیلی است که در شکل 1 نشان داده شده است . دیواره های حفره PEC و ناحیه مورد نظر داخل حفره است که خلاء است.
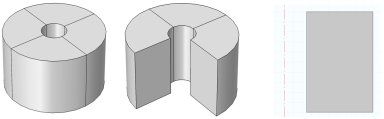
شکل 1: هندسه حفره تشدید. از چپ به راست: نمای کامل، نمای برش 3/4، مقطع در صفحه rz.
مشکل در حوزه فرکانس حل شده است. وابستگی زمانی مفروض ej ω t است ، که در آن ω فرکانس زاویه ای است و با ω = 2 π f به فرکانس f مربوط می شود . شکل هماهنگ زمانی معادله کرل-کورل یک معادله مقدار ویژه همگن در میدان الکتریکی E و مقدار ویژه ناشناخته ω 2 است که در زیر نشان داده شده است.
(1)
از آنجایی که خواص مواد و هندسه متقارن هستند، مدل را می توان با فرمول متقارن محوری دوبعدی حل کرد. حوزه محاسباتی صفحه rz است و متغیرهای وابسته مولفه های استوانه ای میدان الکتریکی Er (r, z ) , E φ ( r , z ) و E z ( r , z ) هستند که به طور کلی عبارتند از ، پیچیده
وابستگی زاویه‌ای میدان به شکل فرض می‌شود 
که m یک عدد صحیح به نام عدد حالت ازیموتال است. شماره حالت azimuthal توسط کاربر مشخص می شود. فرکانس های ویژه برای حفره رزونانس برای m = 0 ، 1 و 2 با استفاده از یک جارو پارامتریک، که شبیه به یک حلقه for است، حل می شود .
که m یک عدد صحیح به نام عدد حالت ازیموتال است. شماره حالت azimuthal توسط کاربر مشخص می شود. فرکانس های ویژه برای حفره رزونانس برای m = 0 ، 1 و 2 با استفاده از یک جارو پارامتریک، که شبیه به یک حلقه for است، حل می شود .وابستگی ترکیبی زمانی و زاویه ای اجزای میدان است 
. کمیت های فیزیکی از متغیرهای وابسته با استفاده از عبارات زیر به دست می آیند، جایی که Re{…} قسمت واقعی کمیت مختلط را نشان می دهد.
. کمیت های فیزیکی از متغیرهای وابسته با استفاده از عبارات زیر به دست می آیند، جایی که Re{…} قسمت واقعی کمیت مختلط را نشان می دهد.(2)
(3)
(4)
فرض کنید E z ( r , z ) کاملا واقعی است، در این صورت معادله قبلی به
(5) 
.
.برای m > 0 ، میدان در جهت +
و برای m < 0 ، میدان در جهت − می چرخد . اگر E z ( r , z ) مختلط باشد و برای سایر اجزای فیلد نیز صدق می کند، این نیز صادق است. این به صراحت در انیمیشن انتهای مثال نشان داده شده است.
و برای m < 0 ، میدان در جهت −
می چرخد . اگر E z ( r , z ) مختلط باشد و برای سایر اجزای فیلد نیز صدق می کند، این نیز صادق است. این به صراحت در انیمیشن انتهای مثال نشان داده شده است.نتایج و بحث
نمودار پیش فرض هنجار میدان الکتریکی است. این نمودار می تواند به عنوان یک ابزار تشخیصی برای تعیین فیزیکی یا جعلی بودن یک حالت خاص استفاده شود. حالت‌های فیزیکی با کمترین فرکانس دارای تغییرات فضایی هستند که با اندازه حفره قابل مقایسه است، در حالی که حالت‌های کاذب دارای تغییرات فضایی هستند که با اندازه مش قابل مقایسه است. هنجار میدان الکتریکی برای 4 حالت با کمترین فرکانس (فیزیکی) زیر در شکل 2 تا شکل 5 رسم شده است .
نمودار فلشی میدان الکتریکی برای حالت m = 1 در 2.122059 گیگاهرتز در شکل 6 نشان داده شده است . این طرح در انتهای مثال متحرک شده است.
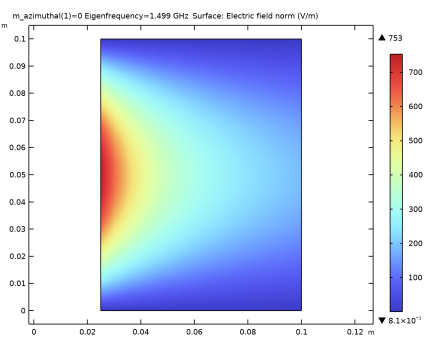
شکل 2: هنجار میدان الکتریکی برای حالت m=0 در 1.499 گیگاهرتز.
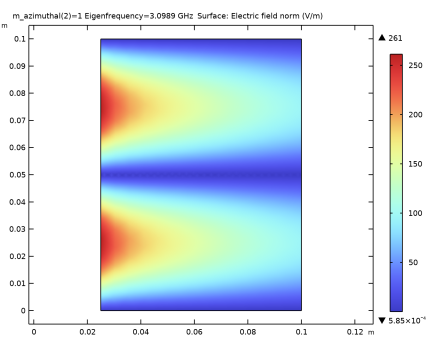
شکل 3: هنجار میدان الکتریکی برای حالت m=1 در 1.692 گیگاهرتز.
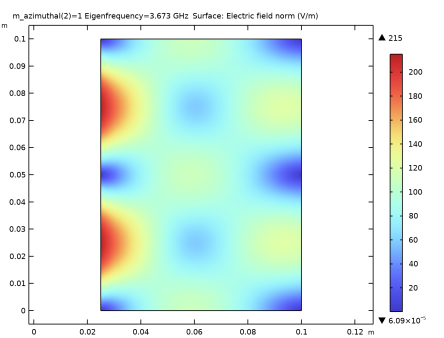
شکل 4: هنجار میدان الکتریکی برای حالت m=1 در 2.122 گیگاهرتز.
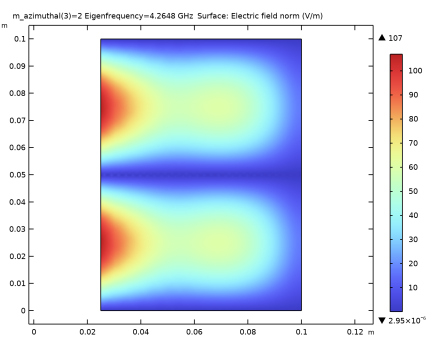
شکل 5: هنجار میدان الکتریکی برای حالت m=2 در 2.076 گیگاهرتز.
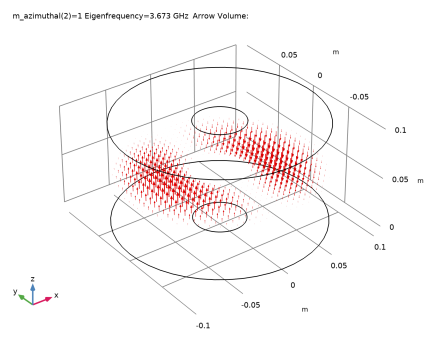
شکل 6: نمودار فلش میدان الکتریکی برای حالت m=1 در 2.122 گیگاهرتز.
با استفاده از جداسازی متغیرها می توان راه حل تحلیلی برای این مسئله به دست آورد. جزئیات اشتقاق را می توان در Ref. 1 . یک معادله استعلایی شامل توابع بسل برای مقدار ویژه k 2 = ω 2 / c 2 وجود دارد . مقادیر 8 حالت در ستون سمت چپ جدول زیر موجود است. ستون سمت راست حاوی مقادیر به دست آمده با استفاده از COMSOL Multiphysics است. نتایج با 1 قسمت در 106 موافق است که تلورانس پیش فرض حل کننده مقدار ویژه است.
معادله ماورایی | COMSOL MULTIPHYSICS |
986.96 | 986.96 |
1257.40 | 1257.42 |
1679.11 | 1679.10 |
1892.55 | 1892.57 |
1978.03 | 1978.03 |
2666.07 | 2666.07 |
2830.13 | 2830.10 |
منابع
1. CM Pinciuc، توابع پایه با محدودیت های واگرایی برای روش اجزای محدود ، Ph.D. پایان نامه، گروه مهندسی برق و کامپیوتر، دانشگاه. تورنتو، 2012، ضمیمه ج، صفحات 174-181.
2. JD Jackson, Classical Electrodynamics , 3rd Edition, John Wiley & Sons, 1999, p. 399 (مساله 8.7).
مسیر کتابخانه برنامه: RF_Module/Verification_Examples/axisymmetric_cavity_resonator
دستورالعمل های مدل سازی
از منوی File ، New را انتخاب کنید .
جدید
در پنجره جدید ، روی 
Model Wizard کلیک کنید .
Model Wizard کلیک کنید .مدل جادوگر
1 | در پنجره Model Wizard ، روی  2D Axismetric کلیک کنید . |
2 | در درخت انتخاب فیزیک ، فرکانس رادیویی > امواج الکترومغناطیسی، دامنه فرکانس (emw) را انتخاب کنید . |
3 | روی افزودن کلیک کنید . |
4 |  روی مطالعه کلیک کنید . |
5 | در درخت انتخاب مطالعه ، General Studies>Eigenfrequency را انتخاب کنید . |
6 |  روی Done کلیک کنید . |
تعاریف جهانی
پارامترهای 1
1 | در پنجره Model Builder ، در قسمت Global Definitions روی Parameters 1 کلیک کنید . |
2 | در پنجره تنظیمات برای پارامترها ، بخش پارامترها را پیدا کنید . |
3 | در جدول تنظیمات زیر را وارد کنید: |
نام | اصطلاح | ارزش | شرح |
آ | 2.5[cm] | 0.025 متر | شعاع داخلی |
ب | 10[cm] | 0.1 متر | شعاع بیرونی |
ارتفاع | 10[cm] | 0.1 متر | ارتفاع |
m_azimuthal | 0 | 0 | شماره حالت ازیموتال |
هندسه 1
یک مستطیل برای هندسه متقارن محور دوبعدی ایجاد کنید.
مستطیل 1 (r1)
1 | در نوار ابزار Geometry ، روی  Rectangle کلیک کنید . |
2 | در پنجره تنظیمات برای Rectangle ، بخش Size and Shape را پیدا کنید . |
3 | در قسمت متن Width ، ba را تایپ کنید . |
4 | در قسمت متن ارتفاع ، ارتفاع را تایپ کنید . |
5 | قسمت Position را پیدا کنید . در قسمت متن r ، a را تایپ کنید . |
6 | در نوار ابزار Geometry ، روی  ساختن همه کلیک کنید . |
هندسه تکمیل شده باید مانند شکل زیر باشد.
مواد
خصوصیات مواد خلاء را به داخل حفره اختصاص دهید.
وکیوم
1 | در پنجره Model Builder ، در قسمت Component 1 (comp1) روی Materials راست کلیک کرده و Blank Material را انتخاب کنید . |
2 | در پنجره تنظیمات برای مواد ، در قسمت نوشتار Label ، Vacuum را تایپ کنید . |
3 | قسمت محتوای مواد را پیدا کنید . در جدول تنظیمات زیر را وارد کنید: |
ویژگی | متغیر | ارزش | واحد | گروه اموال |
مجوز نسبی | epsilonr_iso ; epsilonrii = epsilonr_iso، epsilonrij = 0 | 1 | 1 | پایه ای |
نفوذپذیری نسبی | mur_eye ; murii = mur_iso، murij = 0 | 1 | 1 | پایه ای |
رسانایی الکتریکی | sigma_iso ; sigmaii = sigma_iso، sigmaij = 0 | 0 | S/m | پایه ای |
امواج الکترومغناطیسی، دامنه فرکانس (EMW)
عدد حالت آزیموتال را به پارامتری که در جدول بالا تعریف شده است تغییر دهید.
1 | در پنجره Model Builder ، در قسمت Component 1 (comp1) روی امواج الکترومغناطیسی ، دامنه فرکانس (emw) کلیک کنید . |
2 | در پنجره تنظیمات برای امواج الکترومغناطیسی ، دامنه فرکانس ، بخش شماره موج خارج از صفحه را پیدا کنید . |
3 | در قسمت متن m ، m_azimuthal را تایپ کنید . |
مش 1
1 | در پنجره Model Builder ، در قسمت Component 1 (comp1) روی Mesh 1 کلیک کنید . |
2 | در پنجره تنظیمات مش ، قسمت Physics-Controlled Mesh را پیدا کنید . |
3 | در جدول، تیک Use for Waves Electromagnetic , Frequency Domain (emw) را پاک کنید . |
برای مشکلات امواج الکترومغناطیسی، حداکثر اندازه مش باید کوچکتر از 1/5 طول موج باشد. تغییرات فضایی حالت‌های تشدید کمترین فرکانس با اندازه حفره قابل مقایسه است، بنابراین مش پیش‌فرض نقطه شروع معقولی است. این برای این مدل ساده بسیار دقیق خواهد بود. با این حال، در یک مورد کلی که راه حل های دقیق مشخص نیست، تجزیه و تحلیل پالایش مش مفید است.
4 | در نوار ابزار Home ، روی  Build Mesh کلیک کنید . |
مطالعه 1
حل برای 12 حالت حفره نزدیک به 2 گیگاهرتز، تخمینی برای کمترین فرکانس تشدید بر اساس اندازه حفره. یک مقدار معقول ضروری است تا همه راه حل ها حالت های جعلی نباشند.
مرحله 1: فرکانس ویژه
1 | در پنجره Model Builder ، در زیر مطالعه 1 ، روی Step 1: Eigenfrequency کلیک کنید . |
2 | در پنجره تنظیمات برای Eigenfrequency ، قسمت Study Settings را پیدا کنید . |
3 | کادر بررسی تعداد دلخواه فرکانس ویژه را انتخاب کنید . در فیلد متن مرتبط، 12 را تایپ کنید . |
4 | در قسمت جستجوی فرکانس‌های ویژه اطراف متن، 2[GHz] را تایپ کنید . |
یک جارو پارامتریک روی عدد حالت آزیموتال انجام دهید که شبیه حلقه for است .
جارو پارامتریک
1 | در نوار ابزار مطالعه ، روی  پارامتر Sweep کلیک کنید . |
2 | در پنجره تنظیمات برای جابجایی پارامتری ، بخش تنظیمات مطالعه را پیدا کنید . |
3 |  روی افزودن کلیک کنید . |
4 | در جدول تنظیمات زیر را وارد کنید: |
نام پارامتر | لیست مقادیر پارامتر | واحد پارامتر |
m_azimuthal (شماره حالت ازیموتال) | 0 1 2 |
5 | در نوار ابزار مطالعه ،  روی محاسبه کلیک کنید . |
نتایج
به نمودارهای هنجار میدان الکتریکی نگاه کنید. راه حل های هموار متفاوت حالت های فیزیکی هستند. تنوع فضایی میدان با اندازه حفره قابل مقایسه است. حالت های جعلی دارای تغییرات فضایی قابل مقایسه با اندازه مش هستند. در واقع، فرکانس تشدید و میدان های حالت های جعلی بسیار وابسته به مش هستند. از نمودارها می توان تشخیص داد که حالت تشدید کمترین فرکانس تقریباً 1.49896 گیگاهرتز است.
میدان الکتریکی (emw)
1 | در پنجره Model Builder ، در قسمت Results روی Electric Field (emw) کلیک کنید . |
2 | در پنجره Settings for 2D Plot Group ، بخش Data را پیدا کنید . |
3 | از لیست مقدار پارامتر (m_azimuthal) ، 0 را انتخاب کنید . |
4 | از لیست فرکانس ویژه (گیگاهرتز) ، 1.499 را انتخاب کنید . |
5 | در نوار ابزار Electric Field (emw) ، روی  Plot کلیک کنید . |
این نمودار باید مانند شکل 2 در بالا باشد. سایر نمودارهای دو بعدی را می توان طبق دستورالعمل زیر تولید کرد.
6 | از لیست مقدار پارامتر (m_azimuthal) ، 1 را انتخاب کنید . |
7 | از لیست فرکانس ویژه (گیگاهرتز) ، 3.0989 را انتخاب کنید . |
8 | در نوار ابزار Electric Field (emw) ، روی  Plot کلیک کنید . |
9 | از لیست فرکانس ویژه (گیگاهرتز) ، 3.673 را انتخاب کنید . |
10 | در نوار ابزار Electric Field (emw) ، روی  Plot کلیک کنید . |
11 | از لیست مقدار پارامتر (m_azimuthal) ، 2 را انتخاب کنید . |
12 | از لیست فرکانس ویژه (گیگاهرتز) ، 4.2648 را انتخاب کنید . |
13 | در نوار ابزار Electric Field (emw) ، روی  Plot کلیک کنید . |
k 2 را برای مقایسه با راه حل های به دست آمده از طریق جداسازی متغیرها ارزیابی کنید . عبارت شرطی که در عبارت ظاهر می‌شود تضمین می‌کند که مقادیر غیرصفری فقط برای حالت‌های فیزیکی وجود دارد، یعنی عبارت برای حالت‌های جعلی به صفر می‌رسد.
ارزیابی جهانی 2
1 | در نوار ابزار نتایج ، روی ارزیابی  جهانی کلیک کنید . |
2 | در پنجره تنظیمات برای ارزیابی جهانی ، بخش داده را پیدا کنید . |
3 | از لیست مجموعه داده ، مطالعه 1/ راه حل های پارامتریک 1 (sol2) را انتخاب کنید . |
4 | از لیست ستون های جدول ، راه حل های بیرونی را انتخاب کنید . |
5 | قسمت Expressions را پیدا کنید . در جدول تنظیمات زیر را وارد کنید: |
اصطلاح | واحد | شرح |
(2*pi*freq/c_const)^2 * (فرکانس > 1.4[GHz]) | 1/m^2 |
6 |  روی ارزیابی کلیک کنید . |
انقلاب 2 بعدی
پس از محاسبه راه حل مسئله تقارن محوری دوبعدی، یک چرخش از مجموعه داده دو بعدی تولید می شود. مجموعه داده چرخشی را می توان در نمودارهای سه بعدی استفاده کرد. زاویه شروع را روی 0 و زاویه چرخش را روی 360 قرار دهید.
1 | در پنجره Model Builder ، گره Results>Datasets را گسترش دهید ، سپس روی Revolution 2D کلیک کنید . |
2 | در پنجره تنظیمات برای Revolution 2D ، برای گسترش بخش Revolution Layers کلیک کنید . |
3 | در قسمت متن زاویه شروع ، 0 را تایپ کنید . |
4 | در قسمت نوشتار زاویه انقلاب ، 360 را تایپ کنید . |
5 | برای گسترش بخش Advanced کلیک کنید . تیک Define variables را انتخاب کنید . |
مرحله آخر یک متغیر برای زاویه تعریف می کند، rev1phi ، که می تواند در نمودار فلش سه بعدی میدان الکتریکی استفاده شود.
گروه طرح سه بعدی 2
در نوار ابزار نتایج ، روی 3D Plot Group کلیک کنید .
3D Plot Group کلیک کنید .فلش جلد 1
1 | در نوار ابزار 3D Plot Group 2 ، روی حجم  پیکان کلیک کنید . |
2 | در پنجره تنظیمات برای حجم پیکان ، بخش Expression را پیدا کنید . |
3 | در قسمت متن R-component ، Er*exp(-i*m_azimuthal*rev1phi) را تایپ کنید . |
4 | در قسمت متن PHI-component ، Ephi*exp(-i*m_azimuthal*rev1phi) را تایپ کنید . |
5 | در قسمت متنی Z-component ، Ez*exp(-i*m_azimuthal*rev1phi) را تایپ کنید . |
6 | قسمت تعیین موقعیت پیکان را پیدا کنید . زیربخش X grid points را پیدا کنید . در قسمت متنی Points عدد 30 را تایپ کنید . |
7 | زیربخش نقاط شبکه Y را پیدا کنید . در قسمت متنی Points عدد 30 را تایپ کنید . |
8 | زیربخش نقاط شبکه Z را پیدا کنید . در قسمت متنی Points ، 1 را تایپ کنید . |
9 | در نوار ابزار 3D Plot Group 2 ، روی  Plot کلیک کنید . |
میدان الکتریکی سه بعدی
1 | در پنجره Model Builder ، در قسمت Results روی 3D Plot Group 2 کلیک کنید . |
2 | در پنجره تنظیمات برای گروه طرح سه بعدی ، فیلد الکتریکی سه بعدی را در قسمت نوشتار برچسب تایپ کنید . |
3 | قسمت Data را پیدا کنید . از لیست مقدار پارامتر (m_azimuthal) ، 1 را انتخاب کنید . |
4 | از لیست فرکانس ویژه (گیگاهرتز) ، 3.673 را انتخاب کنید . |
5 | در نوار ابزار 3D Electric Field ، روی  Plot کلیک کنید . |
این نمودار باید مانند شکل 6 در بالا باشد. حالا طرح را به فیلم تبدیل کنید. توجه داشته باشید که برای ایجاد نوسان در یک مجموعه داده دامنه فرکانس در زمان، نوع دنباله روی پسوند داده پویا تنظیم شده است.
انیمیشن 1
1 | در نوار ابزار نتایج ، روی  انیمیشن کلیک کنید و فایل را انتخاب کنید . |
2 | در پنجره تنظیمات برای انیمیشن ، بخش Target را پیدا کنید . |
3 | از لیست هدف ، Player را انتخاب کنید . |
4 | قسمت Scene را پیدا کنید . از لیست موضوع ، میدان الکتریکی سه بعدی را انتخاب کنید . |
5 | قسمت ویرایش انیمیشن را پیدا کنید . از لیست نوع توالی ، پسوند داده پویا را انتخاب کنید . |
6 |  روی دکمه Play در نوار ابزار Graphics کلیک کنید . |
