شرایط فشار، باز و بسته
ساده ترین شرایط مرزی برای تعیین فشار یا سرعت در انتهای لوله است. اینها منجر به شرایط فشار می شوند
و شرط سرعت
و می توانند مستقل از یکدیگر تنظیم شوند و متغیر وابسته دیگر را آزاد بگذاریم. یک زیر کلاس خاص از شرط سرعت، شرط بسته است ، که در آن
مطابق با شرایط دیواره سخت صدا در آکوستیک فشار است. همچنین در اینجا فرض می شود که u 0 = 0 در یک مرز بسته.
وضعیت امپدانس پایانی
در انتهای لولهها رابطه بین فشار و سرعت را میتوان بر حسب امپدانس انتهایی Z تعریف کرد . شرط پایان امپدانس در واسط Pipe Acoustics ارائه شده توسط
(9-9)
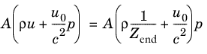
جایی که Z پایان = p / u (واحد SI: (Pa ⋅ s)/m). مدل های مختلفی برای امپدانس انتهایی در رابط های Pipe Acoustics وجود دارد. تنوع به حل شدن معادلات گذرا یا حوزه فرکانس بستگی دارد.
مدلهای امپدانس انتهایی گذرا
در نسخه گذرا رابط فیزیک، امپدانس انتهایی را می توان توسط کاربر تعریف کرد یا تنظیم کرد که یک لوله طولانی بی نهایت را برای شرایط جریان پس زمینه با عدد ماخ کم تقلید کند. در این حالت فرض می شود که لوله با مقطع ثابت A ادامه می یابد و هیچ نیروی خارجی بدنه F و کشیدن τ w وجود ندارد . از آنجایی که امواج صوتی بر اساس طراحی، همیشه با انتهای لوله عادی هستند. برای تعریف رابطه بین فشار و سرعت (امپدانس)، رابطه پراکندگی برای یک موج مسطح باید تعیین شود.
برای انجام این کار شکل موج صفحه فرضی را وارد کنید
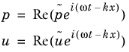
معادله حاکم 9-6 را وارد کرده و روابط مورد نظر را حل کنید. پس از چند دستکاری این نتیجه می شود
با رابطه پراکندگی
(9-10)
این رابطه پراکندگی در k غیر خطی است . در حدی که β A به صفر تمایل دارد و برای اعداد ماخ کوچک M (= u 0 / c )، عبارت به
از این رو، رابطه امپدانس انتهای لوله بی نهایت (محدودیت عدد ماخ کم) خوانده می شود
(9-11)
جایی که علامت جلوی c به جهت انتشار موج بستگی دارد.
مدلهای امپدانس انتهای دامنه فرکانس
در حوزه فرکانس بسیاری از روابط مهندسی برای امپدانس انتهایی یا امپدانس تشعشعی یک لوله یا موجبر وجود دارد. بیشتر روابط فقط برای یک هندسه یا محدوده فرکانسی خاص اعمال می شود. روابط موجود در واسط Pipe Acoustics، Frequency Domain عبارتند از:
• | لوله بی نهایت (محدودیت عدد ماخ کم) : این همان رابطه با مطالعه گذرا است و امپدانس انتهایی با معادله 9-11 ارائه شده است . این را می توان به عنوان امپدانس مشخصه لوله در نظر گرفت. |
• | لوله بی نهایت : این رابطه از رابطه پراکندگی کامل داده شده در معادله 9-10 استفاده می کند و عبارت را به دست می دهد. |
(9-12)
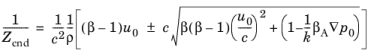
که در آن عدد موج k در سمت راست یک ورودی کاربر است. در حوزه فرکانس یک تخمین خوب برای این کمیت به سادگی ω / c است .
• | لوله فلنج دار، دایره ای : در مورد لوله دایره ای که به یک بافل بی نهایت ختم می شود (یک لوله فلنجی) یک عبارت تحلیلی برای امپدانس تشعشع وجود دارد (رجوع کنید به شماره 1 ). |
(9-13)
که در آن J 1 تابع بسل از مرتبه 1، H 1 تابع Struve از مرتبه 1، a شعاع لوله، و k عدد موج است. تابع Struve مطابق Ref تقریبی شده است. 3 توسط
(9-14)
در حد فرکانس پایین ( ka کوچک ) معادله 9-13 به بیان کلاسیک برای امپدانس تابش کاهش می یابد.
(9-15)
• | لوله فلنج دار، مستطیل شکل : در مورد لوله ای با سطح مقطع مستطیلی (با اضلاع w i و h i ) که به یک بافل بی نهایت ختم می شود (یک لوله فلنج)، امپدانس تابش را می توان به صورت تقریبی تخمین زد. |
(9-16)
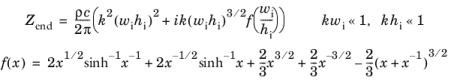
رجوع کنید به رفر. 4 و ر. 5 .
• | لوله بدون فلنج، دایره ای (حد کم کا) : در مورد لوله دایره ای با شعاع که به هوای آزاد ختم می شود، حد کلاسیک پایین کا برای امپدانس تشعشع با |
(9-17)
رجوع کنید به رفر. 1 و رفر. 5 .
• | لوله بدون فلنج، دایره ای : راه حلی برای لوله بدون فلنج برای مواردی وجود دارد که در Ref |
(9-18)
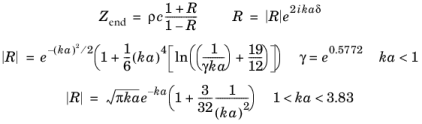
که در آن δ یک تابع درونیابی است که با ادغام عددی برای ka = 0، δ = 0.6133 یافت می شود.
معمول برای چهار رابطه امپدانس تشعشعی این است که آنها فقط زمانی اعمال می شوند که هیچ جریان پس زمینه ای وجود نداشته باشد 0 = 0 (یا حداقل زمانی که بسیار کوچک است).




