معادلات اویلر خطی شده از معادلات اویلر مشتق شده اند، یعنی معادله 5-5 بدون هدایت حرارتی و بدون تلفات ویسکوز. سیال در رابط فیزیک اویلر خطی شده یک گاز ایده آل فرض می شود. معادله انرژی نیز اغلب بر حسب فشار نوشته می شود. این دستکاری با استفاده از دیفرانسیل ترمودینامیکی برای آنتروپی معتبر برای یک گاز ایده آل امکان پذیر است. این رویکرد رایج در ادبیات است. مروری بر معادلات اویلر خطی شده برای مثال در Ref. 12 و رفر. 13 .
معادلات حاکم
خطی سازی معادلات حاکم پس از دستکاری به دست می آید
(5-7)
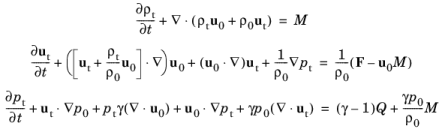
در اینجا، زیرنویس “1” روی متغیرهای اغتشاش صوتی حذف شده است. مشتقات زمانی با ضرب i ω در حوزه فرکانس جایگزین می شوند. و اصطلاحات منبع شامل منبع جرمی M ، نیروی حجمی F و منبع حرارتی Q هستند .
برخی از روابط ایده آل گاز مورد علاقه عبارتند از معادله حالت، ظرفیت گرمایی ویژه و روابط ثابت گاز خاص، و تراکم پذیری همدما و ضرایب همدما انبساط حرارتی:
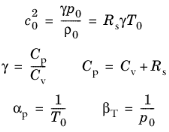
همچنین از معادلات حاکم و روابط ترمودینامیکی به دست می آید که تغییرات صوتی در آنتروپی خاص s و دمای T توسط
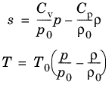
ظرفیت گرمایی ویژه در حجم ثابت و فشار ثابت اغلب با حروف کوچک C مشخص میشود ، در اینجا ما از C بزرگ استفاده میکنیم ، اما آنها کمیتهای خاص هستند. |
ناپایداری ها
هنگامی که معادلات خطی شده اویلر (LE) در حوزه زمان (یا در حوزه فرکانس با حل کننده تکراری) حل می شوند، امواج ناپایداری فیزیکی خطی می توانند ایجاد شوند، به اصطلاح ناپایداری های کلوین-هلمهولتز. آنها ناپایداری هایی هستند که به صورت تصاعدی رشد می کنند زیرا هیچ تلفاتی در معادلات LE وجود ندارد (بدون اتلاف ویسکوز و بدون رسانش گرما). علاوه بر این، آنها توسط غیرخطی بودن در معادلات کامل جریان ناویر-استوکس محدود شدهاند. نشان داده شده است که در موارد خاص، رشد این ناپایداریها را میتوان محدود کرد، در حالی که راهحل صوتی حفظ میشود، با لغو عبارتهایی که شامل گرادیانهای مقادیر متوسط جریان است. این به عنوان تثبیت شرایط گرادیان (GTS) شناخته می شود. جزئیات بیشتر را در Ref. 9 ، ر. 10 و رفر. 11 .
تثبیت سرکوب شرایط گرادیان (GTS) برای معادلات اویلر خطی در دسترس است. اصطلاحات واکنشی شامل گرادیان های جریان پس زمینه را می توان به صورت جداگانه غیرفعال کرد. این اصطلاحات مسئول ایجاد بی ثباتی هستند. همچنین در صورت تمایل می توان تمام اصطلاحات همرفتی را غیرفعال کرد.
نتیجه انرژی
عبارات برای شار انرژی، یعنی بردار شدت آکوستیک، اغلب به عنوان نتیجه انرژی مایرز نامیده می شود، رجوع کنید به Ref. 15 و ر. 16 . بردار شدت لحظه ای I i برای هر دو مدل حوزه گذرا و فرکانس به عنوان تعریف شده است
بردار شدت (متوسط زمان) I در حوزه فرکانس توسط داده می شود
درباره وضعیت مرزی امپدانس
اویلر خطی شده، رابط دامنه فرکانس و اویلر خطی شده، رابط گذرا دارایویژگی فیزیک امپدانس هستند و نظریه آن در اینجا گنجانده شده است.
در حوزه فرکانس، معادله Ingard-Myers ( مراجعه 1 ) بیانی برای سرعت نرمال در مرزی با شرایط امپدانس نرمال می دهد. این به اصطلاح شرایط تقریب فرکانس پایین در حد لایه های مرزی جریان بسیار نازک (در مقایسه با طول موج) است. چنین شرایطی، به عنوان مثال، برای شرایط پوشش متخلخل در کانال ها استفاده می شود ( مرجع 2 ). شرط توسط:
(5-8)
جایی که سطح نرمال n در اینجا به خارج از دامنه اشاره می کند و امپدانس نرمال سطح است.
اگر جریان موازی با شرایط مرزی امپدانس u 0 · n = 0 باشد، برای مثال، جریان لغزش بر روی یک شرایط مرزی امپدانس مکانیکی (همین مورد برای شرایط مرزی دیوار متحرک که در زیر توضیح داده شده است صادق است)، میتوان از فرمولی با مشتق مماسی (  ) برای جمله دوم در سمت راست:
) برای جمله دوم در سمت راست:
که در آن A یک اسکالر دلخواه است.
آخرین عبارت در سمت راست معادله 5-8 را می توان به صورت زیر فرموله کرد:
باز هم، این عبارات به طور قابل توجهی برای موردی که n⋅ u 0 = 0 کاهش می یابد . اگر مرز انحنا نداشته باشد (مرز مسطح) برابر با صفر است. اگر مرز مسطح باشد و از شرایط امپدانس در داخل جریان استفاده شود، برای مثال در شرایط خروجی، آنگاه به شیب نرمال سرعت نرمال به سطح کاهش می یابد.
درباره شرایط مرزی دیوار متحرک
اویلر خطی شده، رابط دامنه فرکانس و رابط اویلر خطی شده، رابط گذرا دارای ویژگی فیزیک دیوار متحرک هستند و نظریه آن در اینجا گنجانده شده است.
معادله مایرز ( مراجعه 1 ) عباراتی را که برای یک شرط مرزی در یک دیوار متحرک استفاده می شود، نشان می دهد. در حوزه فرکانس توسط داده می شود
جابجایی نرمال به سمت داخل توسط
که در آن u n سرعت عادی به سمت داخل است.
در حوزه زمان، شرط سرعت نرمال با استفاده از
که در آن جابجایی نرمال به سمت داخل با v n = – n ⋅ v (واحد SI: m) داده می شود .




