این بخش حاوی اطلاعاتی در مورد انواع تابع شکل موجود (انواع عناصر) است. همچنین به برنامه نویسی عناصر و تابع شکل در کتابچه راهنمای مرجع برنامه نویسی Multiphysics COMSOL مراجعه کنید .
عنصر لاگرانژ
نمونه های قبلی موارد خاصی از عنصر لاگرانژ هستند . یک عدد صحیح مثبت k ، ترتیب عنصر لاگرانژ را در نظر بگیرید. برای عناصر مش سیمپلکس، توابع u در این فضای المان محدود چندجمله ای های تکه ای درجه k هستند . یعنی روی هر عنصر مش u چند جمله ای درجه k است . همچنین در جدول زیر l , m , n اعداد صحیح غیر منفی هستند. به طور کلی، برای یک عنصر مش از نوع T ، u متعلق به فضای تابع شکل لاگرانژ Lag k ( T ) است.، که توسط تک جمله های زیر (یا توابع گویا، در مورد عناصر هرمی) در بر می گیرد:
|
نوع عنصر مش
|
مبنای فضای تابع شکل لاگرانژ
|
|
حاشیه، غیرمتمرکز
|
|
|
مثلث
|
|
|
چهار ضلعی
|
|
|
چهار وجهی
|
|
|
شش وجهی
|
|
|
منشور
|
|
|
هرم
|
|
برای توصیف چنین تابعی کافی است مقادیر آن را در نقاط لاگرانژ از مرتبه k ارائه کنیم . اینها نقاطی هستند که مختصات محلی (عنصر) آنها مضرب صحیح 1 / k هستند . به عنوان مثال، برای یک مش مثلثی در دو بعدی با k = 2 ، این بدان معنی است که شما نقاط گره در گوشه ها و نقاط میانی کناری همه مثلث های مش دارید. برای هر یک از این نقاط گره p i , درجه آزادی U i = u ( p i ) و یک تابع پایه وجود دارد 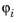 . محدودیت تابع پایه
. محدودیت تابع پایه  به یک عنصر مش تابعی در Lag k است( T ) به طوری که
به یک عنصر مش تابعی در Lag k است( T ) به طوری که 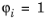 در گره i و
در گره i و 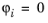 در تمام گره های دیگر. توابع پایه پیوسته هستند و شما دارید
در تمام گره های دیگر. توابع پایه پیوسته هستند و شما دارید
عنصر لاگرانژ مرتبه 1 عنصر خطی نامیده می شود. عنصر لاگرانژ درجه 2 را عنصر درجه دوم می نامند.
عناصر لاگرانژ با انواع عناصر مش در دسترس هستند و رایج ترین نوع عنصر در رابط های فیزیک است. مرتبه k می تواند دلخواه باشد ، اما فرمول های ادغام عددی موجود معمولاً مفید بودن آن را به k≤ 5 ( k ≤ 4 برای مش های چهار وجهی) محدود می کند.

شکل 19-1: نمونه هایی از عناصر لاگرانژ: عنصر شش وجهی مرتبه دوم (27 گره) (سمت چپ) و مرتبه سوم (64 گره) عنصر شش وجهی (راست).
مثال ها
برای راحتی، این مثالها فرمولهای صریح را برای توابع شکل لاگرانژ برای رایجترین انواع عناصر و پایینترین مرتبهها ارائه میکنند.
عناصر مش لبه
برای مرتبه k = 1 ، فضای شکل لاگرانژ دارای بعد 2 است و مبنای زیر دارد:
|
نقطه گره P
|
تابع شکل
|
|
0
|
|
|
1
|
|
برای مرتبه k = 2 فضای شکل لاگرانژ دارای بعد 3 است و اساس زیر را دارد:
|
نقطه گره P
|
تابع شکل
|
|
0
|
|
|
1/2
|
|
|
1
|
|
عناصر مش مثلثی
برای مرتبه k = 1 ، فضای شکل لاگرانژ دارای بعد 3 است و اساس زیر را دارد:
|
نقطه گره P
|
تابع شکل
|
|
(0,0)
|
|
|
(1,0)
|
|
|
(0،1)
|
|
برای مرتبه k = 2 ، فضای شکل لاگرانژ دارای بعد 6 است و مبنای زیر دارد:
|
نقطه گره P
|
تابع شکل
|
|
(0,0)
|
|
|
(1/2,0)
|
|
|
(1,0)
|
|
|
(0,1/2)
|
|
|
(1/2،1/2)
|
|
|
(0،1)
|
|
عناصر مش چهار ضلعی
برای مرتبه k = 1 ، فضای شکل لاگرانژ دارای بعد 4 است و اساس زیر را دارد:
|
نقطه گره P
|
تابع شکل
|
|
(0,0)
|
|
|
(1,0)
|
|
|
(0،1)
|
|
|
(1،1)
|
|
برای مرتبه k = 2 ، فضای شکل لاگرانژ دارای بعد 9 است و مبنای زیر دارد:
|
نقطه گره P
|
تابع شکل
|
|
(0,0)
|
|
|
(1/2,0)
|
|
|
(1,0)
|
|
|
(0,1/2)
|
|
|
(1/2،1/2)
|
|
|
(1,1/2)
|
|
|
(0،1)
|
|
|
(1/2،1)
|
|
|
(1،1)
|
|
عناصر مش چهار وجهی
برای مرتبه k = 1 ، فضای شکل لاگرانژ دارای بعد 4 است و اساس زیر را دارد:
|
نقطه گره P
|
تابع شکل
|
|
(0,0,0)
|
|
|
(1,0,0)
|
|
|
(0،1،0)
|
|
|
(0,0,1)
|
|
برای مرتبه k = 2 ، فضای شکل لاگرانژ دارای بعد 10 است و اساس زیر را دارد:
|
نقطه گره P
|
تابع شکل
|
|
(0,0,0)
|
|
|
(1/2,0,0)
|
|
|
(1,0,0)
|
|
|
(0,1/2,0)
|
|
|
(1/2,1/2,0)
|
|
|
(0،1،0)
|
|
|
(0,0,1/2)
|
|
|
(1/2,0,1/2)
|
|
|
(0,1/2,1/2)
|
|
|
(0,0,1)
|
|
عناصر مش شش وجهی
برای مرتبه k = 1 ، فضای شکل لاگرانژ دارای بعد 8 است و اساس زیر را دارد:
|
نقطه گره P
|
تابع شکل
|
|
(0,0,0)
|
|
|
(1,0,0)
|
|
|
(0،1،0)
|
|
|
(1،1،0)
|
|
|
(0,0,1)
|
|
|
(1،0،1)
|
|
|
(0،1،1)
|
|
|
(1،1،1)
|
|
عنصر لاگرانژ متغیرهای زیر را تعریف می کند. نام پایه را با u نشان دهید و اجازه دهید x و y مختصات فضایی (نه لزوماً متمایز) را نشان دهند. متغیرها ( sdim = بعد فضا و edim = بعد عنصر مش):
|
•
|
تو
|
|
•
|
ux ، به معنی مشتق u نسبت به x ، تعریف شده در edim = sdim
|
|
•
|
uxy ، به معنای مشتق دوم، تعریف شده در edim = sdim
|
|
•
|
uTx ، متغیر مشتق مماسی، به معنای مولفه x پیش بینی مماسی گرادیان، تعریف شده در edim < sdim
|
|
•
|
uTxy ، به معنی xy – جزء برآمدگی مماسی مشتق دوم، تعریف شده زمانی که edim < sdim
|
هنگام محاسبه مشتقات، مختصات فضایی سراسری به صورت چندجملهای از مرتبه درجه (حداکثر) در مختصات محلی بیان میشوند .
|
|
استفاده از عناصر ایزوپارامتری به این معنی است که u در مختصات کلی (اگر k > 1 ) چند جمله ای نیست ، فقط در مختصات محلی است.
|
عنصر SERENDIPITY گره
در هر عنصر مش، توابع موجود در فضای المان محدود سرندیپیتی گرهی زیرمجموعه ای از عناصر لاگرانژ است. برای عناصر مش سیمپلکس، توابع u در این فضای المان محدود چندجمله ای های تکه ای درجه k هستند که k = 2، 3، یا 4. یعنی روی هر عنصر مش u چند جمله ای درجه k است . در جدول زیر، l ، m و n اعداد صحیح غیر منفی هستند. همچنین، یک تابع sl ( i ) (برای مرتبه فوق خطی) تعریف کنید به طوری که sl ( i ) برابر با i باشد ، اگر i > 1; else sl ( i ) = 0. به طور کلی، برای یک عنصر شبکه ای از نوع T ، u متعلق به فضای تابع شکل سرندیپیتی گره ای Ser k ( T ) است که توسط تک جمله های زیر (یا توابع گویا، در مورد عناصر هرم):
|
نوع عنصر مش
|
اساس فضای تابع شکل SERENDIPITY گره
|
|
حاشیه، غیرمتمرکز
|
|
|
مثلث
|
|
|
چهار ضلعی
|
|
|
چهار وجهی
|
|
|
شش وجهی
|
|
|
منشور
|
|
|
هرم
|
|
برای توصیف چنین تابعی کافی است که مقادیر آن را در نقاط سرندیپیتی مرتبه k ارائه کنیم ، جایی که k برابر 2، 3 یا 4 است. این نقاط زیرمجموعه ای از نقاط لاگرانژ هستند (به عنصر لاگرانژ مراجعه کنید ). برای هر یک از این نقاط گره p i , درجه آزادی U i = u ( p i ) و یک تابع پایه وجود دارد 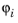 . محدودیت تابع پایه
. محدودیت تابع پایه  به یک عنصر مش تابعی در تاخیر k ( T ) است به طوری که
به یک عنصر مش تابعی در تاخیر k ( T ) است به طوری که 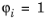 در گره i ، و
در گره i ، و در تمام گره های دیگر توابع پایه پیوسته هستند و شما دارید
در تمام گره های دیگر توابع پایه پیوسته هستند و شما دارید

شکل 19-2: نمونه هایی از عناصر سرندیپیتی: عنصر شش وجهی مرتبه دوم (گره 20) (سمت چپ) و مرتبه سوم (32 گره) عنصر شش وجهی (راست).
عنصر serendipity گره متغیرهای فیلد زیر را تعریف می کند. نام پایه را با u نشان دهید و اجازه دهید x و y مختصات فضایی (نه لزوماً متمایز) را نشان دهند. متغیرها ( sdim = بعد فضا و edim = بعد عنصر مش):
|
•
|
تو
|
|
•
|
ux ، به معنی مشتق u نسبت به x ، که وقتی edim = sdim یا edim = 0 تعریف می شود.
|
|
•
|
uxy به معنای مشتق دوم است که با edim = sdim تعریف می شود
|
|
•
|
uTx ، متغیر مشتق مماسی، به معنای مولفه x پیش بینی مماسی گرادیان، که وقتی 0 < edim < sdim تعریف می شود
|
|
•
|
uTxy ، به معنی xy – جزء برآمدگی مماسی مشتق دوم، تعریف شده زمانی که edim < sdim
|
هنگام محاسبه مشتقات، مختصات فضایی سراسری به صورت چندجملهای از مرتبه درجه (حداکثر) در مختصات محلی بیان میشوند .
عنصر ARGYRIS
برای تابعی که با عناصر لاگرانژ نمایش داده می شود، اولین مشتقات بین عناصر مش می توانند ناپیوسته باشند. در معادلات خاص (به عنوان مثال، معادله بی هارمونیک) این می تواند یک مشکل باشد. عنصر Argyris دارای توابع پایه با مشتقات پیوسته بین مثلث های مش است (فقط در دو بعدی تعریف شده است). مشتق مرتبه دوم در گوشه های مثلث پیوسته است. در هر مثلث، یک تابع u در فضای المان محدود Argyris یک چند جمله ای درجه 5 در مختصات محلی است.
عنصر Argyris فقط با مش های مثلثی موجود است.
هنگام تنظیم شرایط مرزی دیریکله بر روی متغیری که دارای توابع شکل Argyris است، اگر مرز منحنی باشد و از ترتیب محدودیت 5 استفاده شود، یک اثر قفل می تواند رخ دهد. اگر مرز منحنی است از ترتیب محدودیت 4 و برای مرزهای مستقیم از 5 استفاده کنید.
عنصر Argyris درجات آزادی زیر را تعریف می کند (که در آن u نام پایه و x و y نام مختصات فضایی هستند):
|
•
|
تو در گوشه و کنار
|
|
•
|
ux و uy در گوشه ها، به معنی مشتقات u
|
|
•
|
uxx ، uxy و uyy در گوشه ها، به معنی مشتقات دوم
|
|
•
|
u n در نقاط میانی جانبی، به معنای یک مشتق عادی. اگر در امتداد لبه از گوشه ای با عدد راس مش کمتر به گوشه ای با عدد بالاتر حرکت کنید، جهت نرمال به سمت راست است.
|
عنصر Argyris متغیرهای فیلد زیر را تعریف می کند (که در آن sdim = بعد فضا = 2 و edim = بعد عنصر مش):
|
•
|
تو
|
|
•
|
ux ، به معنی مشتق u نسبت به x
|
|
•
|
uxy ، به معنای مشتق دوم، تعریف شده برای edim = sdim و edim = 0
|
|
•
|
uxTy ، متغیر مشتق مماسی، به معنای مؤلفه y از طرح مماسی گرادیان ux ، تعریف شده برای 0 < edim < sdim
|
هنگام محاسبه مشتقات، مختصات فضایی جهانی همیشه با مرتبه شکل 1 در عنصر Argyris بیان می شود.
عنصر هرمیت
در هر عنصر مش، توابع در فضای المان محدود هرمیت مانند عنصر لاگرانژ است، یعنی همه چند جمله ای های درجه (حداکثر) k در مختصات محلی. تفاوت در این است که از DOF ها استفاده می شود. برای عنصر هرمیت، یک DOF u در هر نقطه لاگرانژ درجه k وجود دارد ، به جز در نقاط مجاور گوشه ای از عنصر مش. این DOF ها مقادیر تابع هستند. علاوه بر این، DOF های دیگری برای اولین مشتقات تابع (با توجه به مختصات جهانی) در گوشه ها ( ux و uy) وجود دارند.به صورت دو بعدی). این DOF ها با هم چند جمله ای ها را به طور کامل تعیین می کنند. توابع موجود در فضای اجزای محدود هرمیت مشتقات پیوسته ای بین عناصر مش در رئوس مش دارند. با این حال، در سایر نقاط مشترک برای دو عنصر مش، این مشتقات پیوسته نیستند. شما می توانید عنصر هرمیت را بین عناصر لاگرانژ و آرگریس در نظر بگیرید.
عنصر هرمیت با انواع المان های مش به جز هرم موجود است. ترتیب k ≥ 3 می تواند دلخواه باشد ، اما فرمول های ادغام عددی موجود معمولاً مفید بودن آن را به k≤ 5 (k≤ 4 برای مش های چهار وجهی ) محدود می کند.
هنگام تنظیم شرایط مرزی دیریکله روی متغیری که دارای توابع شکل هرمیت است، اگر مرز منحنی باشد و مرتبه محدودیت cporder با ترتیب عنصر Hermite یکسان باشد، میتواند یک اثر قفلی رخ دهد. این بدان معنی است که مشتق در رئوس مش در مرز به دلیل اجرای شرایط مرزی بیش از حد محدود می شود. برای جلوگیری از این قفل، می توانید cporder را به ترتیب عنصر منهای 1 تعیین کنید.
عنصر هرمیت درجات آزادی زیر را تعریف می کند:
|
•
|
مقدار نام پایه متغیر در هر نقطه گره لاگرانژ که مجاور گوشه ای از عنصر مش نیست.
|
|
•
|
مقادیر اولین مشتقات نام پایه با توجه به مختصات فضایی جهانی در هر گوشه از عنصر مش. نام این مشتقات با الحاق نام مختصات مکانی به نام پایه تشکیل می شود .
|
عنصر Hermite متغیرهای فیلد زیر را تعریف می کند. نام پایه را با u نشان دهید و اجازه دهید x و y مختصات فضایی (نه لزوماً متمایز) را نشان دهند. متغیرها ( sdim = بعد فضا و edim = بعد عنصر مش):
|
•
|
تو
|
|
•
|
ux ، به معنی مشتق u نسبت به x ، که وقتی edim = sdim یا edim = 0 تعریف می شود.
|
|
•
|
uxy به معنای مشتق دوم است که با edim = sdim تعریف می شود
|
|
•
|
uTx ، متغیر مشتق مماسی، به معنای مولفه x پیش بینی مماسی گرادیان، که وقتی 0 < edim < sdim تعریف می شود
|
|
•
|
uTxy ، به معنی xy – جزء برآمدگی مماسی مشتق دوم، تعریف شده زمانی که edim < sdim
|
هنگام محاسبه مشتقات، مختصات فضایی سراسری به صورت چندجملهای از مرتبه درجه (حداکثر) در مختصات محلی بیان میشوند .
عناصر حباب
عناصر حباب دارای توابع شکل هستند که در مرزهای عنصر مش صفر هستند و حداکثر در وسط عنصر مش هستند. تابع شکل (فقط یک عنصر برای هر عنصر مش وجود دارد) با یک چند جملهای پایینترین مرتبه که در مرز عنصر صفر است، تعریف میشود.
عنصر حباب با انواع المان های مش در دسترس است.
عنصر حباب دارای یک درجه آزادی است، نام پایه ، در نقطه میانی عنصر مش.
عنصر حباب متغیرهای فیلد زیر را تعریف می کند. نام پایه را با u نشان دهید و اجازه دهید x و y مختصات فضایی (نه لزوماً متمایز) را نشان دهند. متغیرها ( sdim = بعد فضا و edim = بعد عنصر مش):
|
•
|
u ، تعریف شده زمانی که edim ≤ mdim ، u = 0 اگر edim < mdim .
|
|
•
|
ux به معنای مشتق u نسبت به x است که وقتی edim = mdim = sdim تعریف می شود .
|
|
•
|
u Tx ، متغیر مشتق مماسی، به معنای مولفه x پیش بینی مماسی گرادیان، تعریف می شود که mdim < sdim و edim ≤ mdim . u T x = 0 اگر edim < mdim .
|
|
•
|
u T xy ، به معنای مولفه xy برآمدگی مماسی مشتق دوم، که وقتی mdim < sdim و edim ≤ mdim تعریف می شود . u T xy = 0 اگر edim < mdim .
|
عنصر کرل
در الکترومغناطیسی، عناصر حلقه (که به آنها عناصر برداری یا عناصر Nédélec از نوع اول نیز گفته می شود)) به طور گسترده مورد استفاده قرار می گیرند. هر عنصر مش دارای DOFهایی است که فقط مربوط به اجزای مماسی میدان است. به عنوان مثال، در یک شبکه چهار وجهی به صورت سه بعدی، هر یک از سه یال در یک المان صورت مثلثی دارای درجاتی از آزادی است که مولفه های مماس میدان برداری در جهت یال های مربوطه هستند و در داخل مثلث درجاتی از آزادی که با بردارهای مماس بر خود مثلث مطابقت دارد (اگر ترتیب عناصر به اندازه کافی بالا باشد). در نهایت، در داخل چهار وجهی مش درجاتی از آزادی در تمام جهات مختصات وجود دارد (اگر ترتیب عناصر به اندازه کافی بالا باشد). این بدان معناست که اجزای مماسی میدان برداری در سراسر مرزهای عنصر پیوسته هستند، اما مولفه عادی لزوماً پیوسته نیست.
عناصر فر برای همه انواع عناصر مش در دسترس هستند. ترتیب چند جمله ای عنصر curl می تواند حداکثر هفت در 1D، 2D و 3D باشد.
|
|
هنگام پس پردازش عناصر curl (عناصر برداری)، مشتقات فضایی مرتبه بالاتر فیلدها در دسترس نیستند.
|
شرح مفصل عنصر Curl
رابطه دقیق بین میدان برداری (در واقع یک شکل) و DOFهای عنصر curl بسیار پیچیده است. ما با معرفی برای هر عنصر مش T با بعد d ، فضای تابع شکل برداری محلی Curl k ( T ) را که شامل فیلدهای برداری است 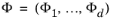 که شرایط زیر را برآورده می کند، شروع می کنیم:
که شرایط زیر را برآورده می کند، شروع می کنیم:
که در آن Lag k ( T ) فضای تابع شکل لاگرانژ است که در بخش توابع شکل لاگرانژ تعریف شده است. یک استثنا وجود دارد؛ برای عناصر مش هرمی، تعریف باید به صورت زیر اصلاح شود:
سپس یک تبدیل بین مختصات محلی و جهانی را برای یک میدان برداری در یک عنصر مش T با بعد d که در فضای بعد D تعبیه شده است، معرفی می کنیم . برای یک فیلد برداری در مختصات جهانی 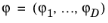 ، فیلد برداری متناظر در مختصات محلی
، فیلد برداری متناظر در مختصات محلی 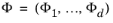 با اجزای تعریف شده توسط
با اجزای تعریف شده توسط
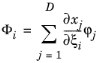
برای عناصر مش با بعد کامل d = D ، این رابطه می تواند معکوس شود تا به دست آید

به طور خاص، اگر T دارای بعد کامل باشد،  وجه یا لبه T باشد ، و
وجه یا لبه T باشد ، و  یک میدان برداری روی T
یک میدان برداری روی T در مختصات محلی باشد، آنگاه می توان یک میدان برداری را محاسبه کرد، و از محدودیت آن به
در مختصات محلی باشد، آنگاه می توان یک میدان برداری را محاسبه کرد، و از محدودیت آن به  یک میدان برداری
یک میدان برداری  در مختصات محلی روی
در مختصات محلی روی  .
.
فقط اجزای میدان بردار مختصات سراسری را 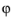 می توان مستقیماً به عنوان متغیر ارزیابی کرد.
می توان مستقیماً به عنوان متغیر ارزیابی کرد.
رابطه بین DOFها و فیلدهای برداری با تعیین در هر عنصر مش تعدادی جفت ( p , v ) تعریف می شود که p یک نقطه در عنصر مش (در مختصات محلی داده شده) و v یک بردار است. سپس DOF ها به صورت تعریف می شوند
اگر تعداد جفت ها در هر عنصر مش از نوع T برابر با بعد Curl k ( T ) انتخاب شود ، مقادیر این DOFها به طور منحصر به فرد فیلد برداری را تعریف می کنند 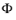 . به طور معمول، برخی از جفت ها ( p ، v ) دارای p در داخل T هستند ، در حالی که برخی دیگر دارای p در برخی از وجه یا لبه ها هستند
. به طور معمول، برخی از جفت ها ( p ، v ) دارای p در داخل T هستند ، در حالی که برخی دیگر دارای p در برخی از وجه یا لبه ها هستند  . راحت است که DOF های مربوط به نقاط اخیر را به عنوان به ارث رسیده از
. راحت است که DOF های مربوط به نقاط اخیر را به عنوان به ارث رسیده از 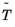 .
.
از آنجایی که ممکن است بیش از یک DOF در یک نقطه p وجود داشته باشد ، نام های DOF دارای پسوندی متشکل از دو عدد صحیح هستند تا DOF های مختلف را در یک نقطه تشخیص دهند.
انتخاب جفت ها ( p , v ) باید جهت هر عنصر مش را در نظر بگیرد. عدم انجام این کار منجر به یک میدان برداری می شود که مولفه مماسی آن در مرز بین عناصر مش تغییر جهت می دهد. این کار با استفاده از شماره گذاری سراسری تمام رئوس مش انجام می شود.
عناصر مش لبه
هر عنصر مش لبه دارای k DOF است. فرض کنید P 0 , P 1 مختصات محلی نقاط انتهایی لبه باشد که به ترتیب افزایش شاخص های رأس مش نوشته می شود (بنابراین P 0 , P 1 نوعی جایگشت از نقاط 0 و 1 در خط واقعی است). فرض کنید v 1 بردار 1 بعدی باشد  . در مختصات محلی، DOF ها در عنصر لبه با جفت های زیر ( p , v ) تعریف می شوند :
. در مختصات محلی، DOF ها در عنصر لبه با جفت های زیر ( p , v ) تعریف می شوند :
|
پ
|
V
|
پسوند نام DOF
|
|
|
|
10
|
عناصر مش مثلثی
هر عنصر مش مثلثی دارای k DOF در هر لبه (به ارث رسیده از عناصر لبه مربوطه) و k ( k – 1 ) DOF در داخل است. فرض کنید P 0 , P 1 , P 2 مختصات محلی رئوس مثلث باشد، به ترتیب افزایش شاخص های رأس مش (بنابراین P 0 , P 1 , P 2 مقداری جایگشت از نقاط (0, 0), (1, 0)، (0، 1)). بگذار  و
و  . سپس DOF های داخلی در این مثلث با جفت های زیر تعریف می شوند ( p , v) :
. سپس DOF های داخلی در این مثلث با جفت های زیر تعریف می شوند ( p , v) :
|
پ
|
V
|
پسوند نام DOF
|
|
|
|
20
|
|
|
|
21
|
عناصر مش چهار ضلعی
هر عنصر مش چهار ضلعی دارای k DOF در هر لبه (به ارث رسیده از عناصر لبه مربوطه) و 2 k ( k – 1 ) DOF در داخل است. فرض کنید P 0 مختصات محلی راس با کمترین شاخص جهانی، P 1 راس دیگر در همان لبه افقی P 0 و P 2 راس دیگر در همان لبه عمودی P 0 باشد (پس P 0 , P 1 ، P 2 زیر مجموعه ای از نقاط (0، 0)، (1، 0)، (0، 1)، (1، 1)) است. اجازه دهید و
و  . سپس DOF های داخلی در این چهار ضلعی با جفت های زیر ( p , v ) تعریف می شوند :
. سپس DOF های داخلی در این چهار ضلعی با جفت های زیر ( p , v ) تعریف می شوند :
|
پ
|
V
|
پسوند نام DOF
|
|
|
|
10
|
|
|
|
10
|
عناصر مش چهار وجهی
هر عنصر مش چهاروجهی k DOF در هر لبه، k ( k – 1 ) DOF در هر وجه و k ( k – 1 ) ( k – 2 ) / 2 DOF در قسمت داخلی دارد. فرض کنید P 0 , P 1 , P 2 , P 3 مختصات محلی رئوس چهار وجهی باشد، به ترتیب افزایش شاخص های رأس مش (بنابراین P 0 , P 1 , P 2 , P 3مقداری جایگشت نقاط (0، 0، 0)، (1، 0، 0)، (0، 1، 0)، (0، 0، 1)) است. اجازه دهید
سپس DOF های داخلی در این چهار وجهی با جفت های زیر ( p , v ) تعریف می شوند :
|
پ
|
V
|
پسوند نام DOF
|
|
|
|
30
|
|
|
|
31
|
|
|
|
32
|
عناصر مش شش وجهی
هر عنصر مش شش وجهی k DOF در هر لبه، 2 k ( k – 1 ) DOF در هر وجه و 3 k ( k – 1 ) 2 DOF در قسمت داخلی دارد. فرض کنید P 0 مختصات محلی راس با کمترین شاخص جهانی باشد و P 1 , P 2 , P 3 رئوس دیگری باشند که فقط در مختصات ξ 1 , ξ 2 , ξ 3 با P 0 تفاوت دارند. اجازه دهید
سپس DOF های داخلی در این شش وجهی با جفت های زیر ( p , v ) تعریف می شوند :
|
پ
|
V
|
پسوند نام DOF
|
|
|
|
10
|
|
|
|
10
|
|
|
|
10
|
عناصر مش منشوری
هر عنصر مش منشوری k DOF در هر لبه، k ( k – 1 ) DOF در هر وجه مثلثی، 2 k ( k – 1 ) DOF در هر وجه چهار ضلعی، و k ( k – 1 ) ( 3 k – 4 )/ دارد. 2 DOF در فضای داخلی. فرض کنید P 0 مختصات محلی راس با کمترین شاخص جهانی باشد، P 1 , P 2 دو راس دیگر در همان صورت مثلثی P باشد.0 ، شماره گذاری شده است به طوری که P 1 دارای شاخص کمتری از P 2 است ، و اجازه دهید P 3 سومین نقطه ای باشد که توسط یک یال به P 0 متصل می شود. اجازه دهید
سپس DOF های داخلی در این منشور با جفت های زیر ( p , v ) تعریف می شوند :
|
پ
|
V
|
پسوند نام DOF
|
|
|
|
20
|
|
|
|
21
|
|
|
|
10
|
عناصر مش هرمی
هر عنصر مش هرم دارای k DOF در هر لبه، k ( k – 1 ) DOF در هر وجه مثلثی، 2 k ( k – 1 ) DOF در وجه چهار ضلعی، و k ( k – 1 ) ( 2 k – 1 )/ است. 2 DOF در فضای داخلی. اجازه دهید v 1 = ( 1 , 0 , 0 ) , v 2 = ( 0 , 1 , 0) و v 3 = ( 0 , 0 , 1 ) . سپس DOF های داخلی در این هرم با جفت های زیر ( p , v ) تعریف می شوند :
|
پ
|
V
|
پسوند نام DOF
|
|
|
|
30
|
|
|
|
31
|
|
|
|
32
|
مثال ها
برای سهولت در اینجا فرمول های صریح برای توابع شکل Curl برای کمترین مرتبه و رایج ترین عناصر مش ارائه می دهیم. برای هر نوع عنصر، تابع شکل مربوط به هر DOF در مختصات محلی برای ترتیب خاصی از رئوس عنصر مش نوشته می شود. برای اعداد دیگر، تفاوت این است که بردار v برای برخی از DOF ها تغییر جهت می دهد. برای DOF با پسوند 10 این به سادگی به این معنی است که توابع شکل مربوطه تغییر علامت می دهند. سایر توابع شکل ممکن است با ترکیبی خطی از توابع شکل مربوط به DOF در همان نقطه گره جایگزین شوند.
عناصر مش مثلثی
در فرمول های زیر فرض می شود که رئوس مثلث به ترتیب افزایش شاخص رأس مش دارای مختصات محلی (0، 0)، (1، 0)، (0، 1) هستند.
برای مرتبه k = 1، فضای شکل Curl دارای بعد 3 است و اساس زیر را دارد:
|
پ
|
V
|
پسوند نام DOF
|
فیلد برداری محلی
|
|
(1/2,0)
|
(1,0)
|
10
|
|
|
(0,1/2)
|
(0،1)
|
10
|
|
|
(1/2،1/2)
|
(-1،1)
|
10
|
|
برای مرتبه k = 2، فضای شکل Curl دارای بعد 8 است و اساس زیر را دارد:
|
پ
|
V
|
پسوند نام DOF
|
فیلد برداری محلی
|
|
(1/3,0)
|
(1,0)
|
10
|
|
|
(2/3,0)
|
(1,0)
|
10
|
|
|
(0,1/3)
|
(0،1)
|
10
|
|
|
(0,2/3)
|
(0،1)
|
10
|
|
|
(2/3،1/3)
|
(-1،1)
|
10
|
|
|
(1/3،2/3)
|
(-1،1)
|
10
|
|
|
(1/3،1/3)
|
(1,0)
|
20
|
|
|
(1/3،1/3)
|
(0،1)
|
21
|
|
عناصر مش چهار ضلعی
فرمول های زیر فرض می کنند که رئوس چهارضلعی به ترتیب افزایش شاخص رأس مش دارای مختصات محلی (0، 0)، (1، 0)، (0، 1)، (1، 1) هستند.
برای مرتبه k = 1 فضای شکل Curl دارای بعد 4 است و اساس زیر را دارد:
|
پ
|
V
|
پسوند نام DOF
|
فیلد برداری محلی
|
|
(1/2,0)
|
(1,0)
|
10
|
|
|
(1/2،1)
|
(1,0)
|
10
|
|
|
(0,1/2)
|
(0،1)
|
10
|
|
|
(1,1/2)
|
(0،1)
|
10
|
|
برای مرتبه k = 2 فضای شکل Curl دارای بعد 12 است و اساس زیر را دارد:
|
پ
|
V
|
پسوند نام DOF
|
فیلد برداری محلی
|
|
(1/3,0)
|
(1,0)
|
10
|
|
|
(2/3,0)
|
(1,0)
|
10
|
|
|
(1/3،1)
|
(1,0)
|
10
|
|
|
(2/3،1)
|
(1,0)
|
10
|
|
|
(0,1/3)
|
(0،1)
|
10
|
|
|
(0,2/3)
|
(0،1)
|
10
|
|
|
(1,1/3)
|
(0،1)
|
10
|
|
|
(1,2/3)
|
(0،1)
|
10
|
|
|
(1/3،1/2)
|
(1,0)
|
10
|
|
|
(2/3،1/2)
|
(1,0)
|
10
|
|
|
(1/2،1/3)
|
(0،1)
|
10
|
|
|
(1/2,2/3)
|
(0،1)
|
10
|
|
عناصر مش چهار وجهی
در فرمول های زیر فرض می شود که رئوس چهار وجهی به ترتیب افزایش شاخص رأس مش دارای مختصات محلی (0، 0، 0)، (1، 0، 0)، (0، 1، 0)، (0، 0) هستند. ، 1).
برای مرتبه k = 1 فضای شکل Curl دارای بعد 6 است و مبنای زیر دارد:
|
پ
|
V
|
پسوند نام DOF
|
فیلد برداری محلی
|
|
(1/2,0,0)
|
(1,0,0)
|
10
|
|
|
(0,1/2,0)
|
(0،1،0)
|
10
|
|
|
(0,0,1/2)
|
(0,0,1)
|
10
|
|
|
(1/2,1/2,0)
|
(-1،1،0)
|
10
|
|
|
(1/2,0,1/2)
|
(-1،0،1)
|
10
|
|
|
(0,1/2,1/2)
|
(0,-1,1)
|
10
|
|
عناصر مش شش وجهی
در فرمول های زیر فرض می شود که رئوس شش وجهی به ترتیب افزایش شاخص رأس مش دارای مختصات محلی (0، 0، 0)، (1، 0، 0)، (0، 1، 0)، (1، 1) هستند. ، 0)، (0، 0، 1)، (1، 0، 1)، (0، 1، 1)، (1، 1، 1).
برای مرتبه k = 1 فضای شکل Curl دارای بعد 12 است و اساس زیر را دارد:
|
پ
|
V
|
پسوند نام DOF
|
فیلد برداری محلی
|
|
(1/2,0,0)
|
(1,0,0)
|
10
|
|
|
(1/2،1،0)
|
(1,0,0)
|
10
|
|
|
(1/2،0،1)
|
(1,0,0)
|
10
|
|
|
(1/2،1،1)
|
(1,0,0)
|
10
|
|
|
(0,1/2,0)
|
(0،1،0)
|
10
|
|
|
(1,1/2,0)
|
(0،1،0)
|
10
|
|
|
(0,1/2,1)
|
(0،1،0)
|
10
|
|
|
(1,1/2,1)
|
(0،1،0)
|
10
|
|
|
(0,0,1/2)
|
(0,0,1)
|
10
|
|
|
(1,0,1/2)
|
(0,0,1)
|
10
|
|
|
(0،1،1/2)
|
(0,0,1)
|
10
|
|
|
(1،1،1/2)
|
(0,0,1)
|
10
|
|
عنصر curl درجات آزادی زیر را تعریف می کند: dofbasename d c ، که در آن d = 1 برای DOF ها در داخل یک یال، d = 2 برای DOF ها در داخل یک سطح، و غیره، و c عددی بین 0 و d − 1 .
عنصر curl متغیرهای فیلد زیر را تعریف می کند (که در آن comp یک نام مؤلفه از compnames است ، و dcomp یک مؤلفه از dcompnames است ، sdim = بعد فضا و edim = بعد عنصر مش):
|
•
|
comp ، به معنی جزء بردار است که با edim = sdim تعریف می شود .
|
|
•
|
t comp ، به معنای یکی از اجزای طرح مماس بردار بر روی عنصر مش، که با edim < sdim تعریف می شود .
|
|
•
|
comp x ، به معنی مشتق جزء بردار با توجه به مختصات فضایی سراسری x ، که با edim = sdim تعریف می شود .
|
|
•
|
t comp Tx ، متغیر مشتق مماسی، به معنی جزء x از طرح گرادیان t comp بر روی عنصر مش، که با edim < sdim تعریف میشود . در اینجا x نام مختصات فضایی است.
|
|
•
|
dcomp ، به معنی مؤلفه ای از گرادیان ضد متقارن، که با edim = sdim تعریف می شود .
|
|
•
|
t dcomp ، به معنی یکی از مولفههای پیشبینی مماسی گرادیان ضد متقارن بر روی عنصر مش، که با edim < sdim تعریف میشود .
|
به دلایل عملکرد، از dcomp در عباراتی که شامل curl هستند به جای نوشتن آن به عنوان تفاوت دو جزء گرادیان استفاده کنید.
برای محاسبه مولفهها، مختصات فضایی سراسری به صورت چندجملهای از مرتبه درجه (حداکثر) در مختصات محلی بیان میشوند .
عنصر CURL TYPE 2
عنصر curl type 2 (که عناصر Nédélec از نوع دوم نیز نامیده می شود ) شبیه عنصر curl است که دارای DOFهای مربوط به اجزای مماسی میدان است. تفاوت اصلی این است که عنصر curl type 2 دارای نظم های چند جمله ای کامل در تمام جهات برای هر جزء میدان است. تئوری عناصر curl type 2 در Ref. 1 و رفر. 2 .
عنصر curl type 2 فقط برای عناصر مش سیمپلکس موجود است. ترتیب چند جمله ای عناصر curl type 2 حداکثر می تواند هفت در یک بعدی، دو بعدی و سه بعدی باشد. با DOF های اضافی معرفی شده توسط عنصر curl type 2، وضوح هر جزء فیلد بهبود می یابد، در حالی که پیچش میدان در مقایسه با عنصر curl با همان ترتیب بدون تغییر باقی می ماند.
استفاده از عنصر curl type 2 مانند عنصر curl است که در بالا توضیح داده شد.
عناصر لاگرانژ ناپیوسته و عناصر لاگرانژ ناپیوسته گرهی
توابع در فضای عناصر لاگرانژ ناپیوسته مانند عنصر لاگرانژ استاندارد است، با این تفاوت که توابع پایه بین عناصر مش ناپیوسته هستند. این عناصر در دو نوع موجود هستند: عناصر لاگرانژ ناپیوسته و عناصر لاگرانژ ناپیوسته گرهی . تفاوت بین این دو در این است که دومی با توجه به تخمینهای خطای درونیابی مشخص، درجههای آزادی را بر روی مشهای مثلثی و چهاروجهی قرار میدهد، در حالی که اولی روی همه انواع عناصر مش با مرتبه چند جملهای دلخواه k موجود است .
عنصر ناپیوسته متغیرهای فیلد زیر را تعریف می کند. نام پایه را با u نشان دهید و اجازه دهید x نشان دهنده مختصات مکانی باشد. متغیرها عبارتند از ( edim بعد عنصر مش است):
|
•
|
u زمانی که edim = mdim تعریف می شود .
|
|
•
|
ux به معنای مشتق u نسبت به x است که وقتی edim = mdim = sdim تعریف می شود .
|
|
•
|
uTx ، متغیر مشتق مماسی، به معنای مشتق u نسبت به x ، که وقتی edim = mdim < sdim تعریف میشود .
|
عناصر چگالی
اگر عنصر مش انحنا نداشته باشد، عملکردها در فضای عناصر چگالی مانند عنصر ناپیوسته است. اگر عنصر منحنی باشد، توابع چگالی ترتیب داده شده را در مختصات محلی تعریف می کنند و مقدار در مختصات جهانی به تبدیل بین مختصات محلی و جهانی بستگی دارد. مقادیر DOF متناسب با حجم عناصر مش است.
عناصر ناپیوسته با انواع المان های مش در دسترس هستند. مرتبه k می تواند دلخواه باشد ، اما فرمول های ادغام عددی موجود معمولاً مفید بودن آن را به k≤ 5 ( k ≤ 4 برای مش های چهار وجهی) محدود می کند.
عنصر چگالی متغیرهای فیلد زیر را تعریف می کند. نام پایه را با u نشان دهید و اجازه دهید x نشان دهنده مختصات مکانی باشد. متغیرها عبارتند از ( edim بعد عنصر مش است):
|
•
|
u زمانی که edim = sdim تعریف می شود .
|
|
•
|
ux به معنی مشتق u نسبت به x است که وقتی edim = sdim تعریف می شود .
|
عناصر داده نقطه گاوس
عناصر داده نقطه گاوس به معنای معمول توابع شکل نیستند. در عوض، آنها درجات آزادی گسسته مرتبط با نقاط گاوس را که در یک قاعده ادغام یک نظم معین استفاده می شود، تعریف می کنند. برای در دسترس قرار دادن این درجات آزادی برای ارزیابی و استفاده در معادلات، یک متغیر میدانی با همان نام درجه آزادی نیز تعریف شده است. این میدان را می توان در هر نقطه از عنصر ارزیابی کرد، اما به سادگی تا درجه آزادی در نزدیکترین نقطه گاوس ارزیابی می شود.
برای مثال، از عناصر داده نقطه گاوس برای ذخیره مقادیر تاریخی در نقاط ادغام در مدلهای دارای پسماند، یا حل یک معادله ضمنی برای یک ویژگی ماده در هر نقطه استفاده کنید. اطمینان حاصل کنید که از عناصری با همان ترتیب قانون یکپارچه سازی استفاده شده برای مونتاژ PDE اصلی استفاده می کنید، معمولاً دو برابر ترتیب گسسته سازی متغیرهای وابسته اصلی. این تضمین میکند که دادههای نقطه گاوس واقعاً بهعنوان یک کمیت محلی واقعاً بدون هیچگونه همبستگی مکانی رفتار میکنند.
عنصر داده نقطه گاوس متغیر فیلد زیر را تعریف می کند. Basename را با u نشان دهید و اجازه دهید edim بعد ارزیابی باشد: u ، تعریف شده زمانی که edim <= mdim .
عناصر واگرایی
برای مدلسازی میدانهای B (چگالی شار مغناطیسی) و D (جابجایی الکتریکی) در الکترومغناطیسی، عناصر واگرایی (که عناصر Raviart-Thomas نیز نامیده میشوند ) مفید هستند. DOFها در مرز یک عنصر مش با اجزای عادی میدان مطابقت دارند. علاوه بر این، DOFهای مربوط به تمام اجزای میدان برداری در داخل عنصر مش ابعاد sdim وجود دارد.(اگر سفارش به اندازه کافی بالا باشد). این بدان معناست که مولفه عادی میدان برداری در سراسر مرزهای عنصر پیوسته است، اما مولفه های مماسی لزوماً پیوسته نیستند. این همچنین نشان می دهد که واگرایی میدان برداری یک تابع انتگرال پذیر است، بنابراین این عناصر برای معادلات با استفاده از واگرایی میدان برداری مناسب هستند.
عنصر واگرایی با انواع المان های مش به جز اهرام موجود است. ترتیب چند جمله ای عنصر واگرایی حداکثر می تواند هفت در یک بعدی، دو بعدی و سه بعدی باشد.
عنصر واگرایی درجات آزادی زیر را تعریف می کند: dofbasename در مرزهای عنصر، و dofbasename sdim c , c = 0 , …, sdim – 1 برای DOF ها در داخل.
عنصر واگرایی متغیرهای فیلد زیر را تعریف می کند (که در آن comp یک نام مؤلفه از compnames است ، divname عبارت است از divname ، sdim = بعد فضا و edim = بعد عنصر مش):
|
•
|
comp ، به معنی جزء بردار است که با edim = sdim تعریف می شود .
|
|
•
|
n comp ، به معنی یکی از اجزای طرح بردار بر روی عنصر معمولی مش است که وقتی edim = sdim – 1 تعریف می شود .
|
|
•
|
comp x ، به معنی مشتق جزء بردار با توجه به مختصات فضایی سراسری x ، که با edim = sdim تعریف می شود .
|
|
•
|
n comp T x ، متغیر مشتق مماسی، به معنی جزء x از طرح شیب n comp بر روی عنصر مش، که با edim < sdim تعریف میشود . در اینجا x نام مختصات فضایی است. n comp T x = 0 .
|
|
•
|
divname به معنای واگرایی فیلد برداری است.
|
به دلایل عملکرد، از divname در عبارات مربوط به واگرایی استفاده کنید نه اینکه آن را به عنوان مجموع اجزای گرادیان sdim بنویسید. برای محاسبه مولفهها، مختصات فضایی سراسری به صورت چندجملهای از مرتبه درجه (حداکثر) در مختصات محلی بیان میشوند .
عناصر واگرایی نوع 2
عناصر واگرایی نوع 2 (که عناصر Brezzi-Douglas-Marini نیز نامیده می شوند ) شبیه عناصر واگرایی هستند که DOF ها را در مرز یک عنصر مش مطابق با اجزای عادی میدان تعریف می کنند. مؤلفه عادی میدان برداری در سراسر مرزهای عنصر پیوسته است، اما مؤلفه های مماسی لزوماً پیوسته نیستند. تفاوت اصلی این است که عناصر واگرایی نوع 2 دارای نظم چند جمله ای کامل در تمام جهات برای هر جزء میدان هستند. نظریه واگرایی عناصر نوع 2 در Ref. 2 .
عناصر واگرایی نوع 2 فقط برای عناصر مش سیمپلکس موجود هستند. ترتیب چند جمله ای عناصر واگرایی نوع 2 حداکثر می تواند هفت در یک بعدی، دو بعدی و سه بعدی باشد. در مقایسه با عناصر واگرایی، عناصر واگرایی نوع 2 DOF های بیشتری را برای بهبود وضوح هر جزء میدان معرفی می کنند. با این حال، واگرایی میدان برای این دو نوع عنصر واگرایی از همان ترتیب بدون تغییر باقی میماند.
استفاده از عناصر واگرایی نوع 2 همانند عناصر واگرایی است که در بالا توضیح داده شد.




